【培优版】北师大版数学九上1.1菱形的性质与判定 同步练习
试卷更新日期:2024-06-29 类型:同步测试
一、选择题
-
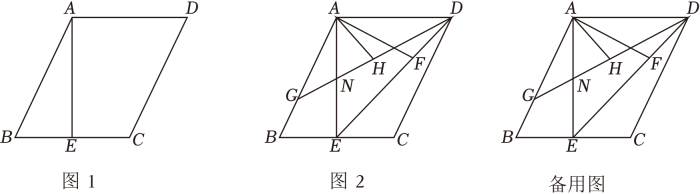
1. 如图,等腰直角三角形中, , 于 , 的平分线分别交 , 于、两点,为的中点,延长交于点 , 连接 , . 下列结论:①;②;③是等边三角形;④;⑤四边形是菱形,正确结论的序号是( )
 A、②④⑤ B、①②③④⑤ C、①③④ D、①②④⑤2. 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,点E为垂足,连接DF,则∠CDF为( )
A、②④⑤ B、①②③④⑤ C、①③④ D、①②④⑤2. 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,点E为垂足,连接DF,则∠CDF为( ) A、80° B、70° C、65° D、60°3. 如图,在菱形中, , O为对角线的交点.将菱形绕点O逆时针旋转得到菱形 , 两个菱形的公共点为E , F , G , H.对八边形给出下面四个结论:
A、80° B、70° C、65° D、60°3. 如图,在菱形中, , O为对角线的交点.将菱形绕点O逆时针旋转得到菱形 , 两个菱形的公共点为E , F , G , H.对八边形给出下面四个结论:
①该八边形各边长都相等;
②该八边形各内角都相等;
③点O到该八边形各顶点的距离都相等;
④点O到该八边形各边所在直线的距离都相等.
上述结论中,所有正确结论的序号是( )
A、①③ B、①④ C、②③ D、②④4. 如图,菱形中, , , 点P , Q , K分别为线段上的任意一点,则的最小值为( ). A、1 B、 C、2 D、5. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
A、1 B、 C、2 D、5. 如图,菱形中, , 与交于点 , 为延长线上的一点,且 , 连接分别交 , 于点、 , 连接 , 则下列结论:( )
;与全等的三角形共有个;
;由点、、、构成的四边形是菱形.
A、 B、 C、 D、二、填空题
-
6. 如图,在菱形中, , , 为边上一动点,将沿折叠为 , 为边上一点, , 则的最小值为 .
 7. 如图,在菱形ABCD中,∠C=60°,AB=2,延长BA至点E,使AE=1,现以点D为圆心,以DE的长为半径画弧,与直线BC相交于点M,则CM的长为.
7. 如图,在菱形ABCD中,∠C=60°,AB=2,延长BA至点E,使AE=1,现以点D为圆心,以DE的长为半径画弧,与直线BC相交于点M,则CM的长为. 8. 如图,在菱形ABCD中,对角线AC,BD交于点O,点E为AB的中点,点F在OD上,DF=OF,连接EF交OA于点G,若OG=1,连接CE, S△BEC=12,则线段CE的长为 .
8. 如图,在菱形ABCD中,对角线AC,BD交于点O,点E为AB的中点,点F在OD上,DF=OF,连接EF交OA于点G,若OG=1,连接CE, S△BEC=12,则线段CE的长为 . 9. 已知直线l的解析式为y=2x+2,菱形AOBA1 , AO1B1A2 , A2O2B2A3 , …按图所示的方式放置,顶点A , A1 , A2 , A3 , …均在直线l上,顶点O , O1 , O2 , …均在x轴上,则点的坐标是 .
9. 已知直线l的解析式为y=2x+2,菱形AOBA1 , AO1B1A2 , A2O2B2A3 , …按图所示的方式放置,顶点A , A1 , A2 , A3 , …均在直线l上,顶点O , O1 , O2 , …均在x轴上,则点的坐标是 .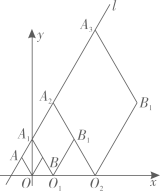 10. 如图,菱形中, , M为边上的一点,将菱形沿折叠后,点A恰好落在的中点E处,则 .
10. 如图,菱形中, , M为边上的一点,将菱形沿折叠后,点A恰好落在的中点E处,则 .
三、解答题
-
11. 如图,菱形中, , E为边上一点,点F在的延长线上, , 作点F关于直线的对称点G , 连接 .
 (1)、依题意补全图形,并证明;(2)、用等式表示之间的数量关系,并证明.12. 如图,在菱形ABCD中,F为边AB的中点,FC与对角线BD相交于点C,过点G作GE⊥BC于点E,∠ADB=∠FCB.求证:
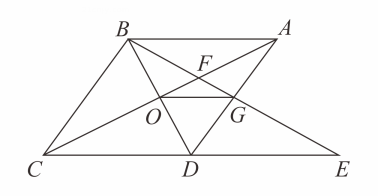
(1)、依题意补全图形,并证明;(2)、用等式表示之间的数量关系,并证明.12. 如图,在菱形ABCD中,F为边AB的中点,FC与对角线BD相交于点C,过点G作GE⊥BC于点E,∠ADB=∠FCB.求证: (1)、AB=2BE;(2)、DG=CF+GE.13. 如图,在中,CE平分 , 交AD于点E,DF平分 , 交BC于点F,CE与DF交于点 , 连结EF,BP
(1)、AB=2BE;(2)、DG=CF+GE.13. 如图,在中,CE平分 , 交AD于点E,DF平分 , 交BC于点F,CE与DF交于点 , 连结EF,BP (1)、求证:四边形CDEF是菱形.(2)、若AB=2,BC=3,∠A=120°,求BP的值.
(1)、求证:四边形CDEF是菱形.(2)、若AB=2,BC=3,∠A=120°,求BP的值.