人教版八年级上学期数学课时进阶测试11.3多边形及其内角和（三阶）
试卷更新日期：2024-06-28 类型：同步测试
一、选择题
-
1. 一副三角尺如图所示摆放，则与的数量关系为（ ）
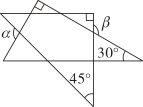A、 B、 C、 D、2. 将一长方形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角和之和不可能是（ ）A、360° B、540° C、720° D、730°3. 一个多边形最少可分割成五个三角形，则它是（ ）边形A、8 B、7 C、6 D、54. 一个多边形的每一个外角都等于且小于45°，那么这个多边形的边数最少是（ ）A、7条 B、8条 C、9条 D、10条5. 如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P=（ ）
A、90°﹣ α B、90°+ α C、 D、360°﹣α6. 连接多边形的一个顶点与其他顶点的线段把这个多边形分成了6个三角形，则原多边形是（ ）边形．A、五 B、六 C、七 D、八7. 下列说法中，①三角形的内角中最多有一个钝角；②三角形的中线将三角形分成面积相等的两部分；③从n边形的一个顶点可以引（n-3）条对角线，把n边形分成（n-2）个三角形，因此，n边形的内角和是（n-2）•180°；④六边形的对角线有7条，正确的个数有（ ）A、4个 B、3个 C、2个 D、1个8. 如图，把△ABC纸片沿DE折叠，当点A在四边形BCDE的外部时，记∠AEB为∠1，∠ADC为∠2，则∠A、∠1与∠2的数量关系，结论正确的是（ ）
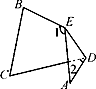A、∠1＝∠2＋∠A B、∠1＝2∠A＋∠2 C、∠1＝2∠2＋2∠A D、2∠1＝∠2＋∠A二、填空题
-
9. 如图，D是△ABC内一点，连接AD、BD、CD ， P是∠BDC的角平分线的反向延长线上的一点，连接BP ， ∠ABP＝2∠PBD ， △ABC和△ACD的外角平分线相交于点Q ， 若∠Q＝45，∠BDC＝4∠ABD ， 则∠P的度数为 ．
10. 一个多边形截去一个角后，所形成的一个新多边形的内角和为2520°，则原多边形有条边。11. 过N边形的一个顶点有7条对角线，M边形有2条对角线、S边形没有对角线，则（n﹣m）s= ．12.如图，已知四边形ABCD中，∠C=72°，∠D=81°．沿EF折叠四边形，使点A、B分别落在四边形内部的点A′、B′处，则∠1+∠2=°．
13. 如图，∠1+∠2+∠3+∠4+∠5+∠6+∠7＝ ．
三、综合题
-
14. 如图①，∠1、∠2是四边形ABCD的两个不相邻的外角．
(1)、猜想并说明∠1+∠2与∠A、∠C的数量关系；(2)、如图②，在四边形ABCD中，∠ABC与∠ADC的平分线交于点O．若∠A＝58°，∠C＝152°，求∠BOD的度数；(3)、如图③，BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线．请直接写出∠A、∠C与∠O的数量关系．15.
(1)、如图1，∠ADC=120°，∠BCD=140°，∠DAB和∠CBE的平分线交于点F，则∠AFB的度数是；(2)、如图2，若∠ADC= ， ∠BCD= ， 且 ， ∠DAB和∠CBE的平分线交于点F，则∠AFB=（用含 ， 的代数式表示）；(3)、如图3，∠ADC= ， ∠BCD= ， 当∠DAB和∠CBE的平分线AG，BH平行时， ， 应该满足怎样的数量关系？请说明理由；(4)、如果将（2）中的条件改为 ， 再分别作∠DAB和∠CBE的平分线，∠AFB与 ， 满足怎样的数量关系？请画出图形并直接写出结论.