【基础版】新北师大版(2024)数学七上1.2从立体图形到平面图形
试卷更新日期：2024-06-27 类型：同步测试
一、选择题
-
1. 下列几何体中，其三视图的主视图和左视图都为矩形的是（ ）A、
B、
C、
D、
2. 古代中国诸多技艺均领先世界.榫卯结构就是其中之一，榫卯是在两个木构件上所采用的一种凹凸结合的连接方式.凸出部分叫榫（或榫头），凹进部分叫卯（或榫眼、榫槽），榫和卯咬合，起到连接作用，右图是某个部件“榫”的实物图，它的主视图是( )
A、
B、
C、
D、
二、填空题
-
3. 将如图所示的长方体用过的平面切割，得到的两个几何体是 ．
4. 用一个平面去截长方体，三棱柱，圆柱，和圆锥，其中不能截出三角形的几何体.5. 如图所示的是一个正方体的表面展开图，折成正方体后其相对面上的两个数互为相反数，a-b= ．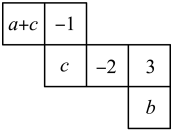
三、解答题
-
6. 某产品的形状是长方体，长为 ，它的展开图如图所示，求长方体的体积.
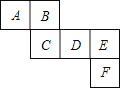
7.如图是一个正方体的表面展开图，请回答下列问题：
（1）与面B、C相对的面分别是 ；
（2）若A=a3+a2b+3，B=a2b﹣3，C=a3﹣1，D=﹣（a2b﹣6），且相对两个面所表示的代数式的和都相等，求E、F分别代表的代数式．
8. 在我们的课本第142页“4.4课题学习”中，有包装纸盒的设计制作方法．下图是设计师为“XX快递”设计的长方体包装盒的轮廓草图，其中长30cm、宽20cm、高18cm，正面有“快递”字样，上面有“上”字样，棱AB是上盖的掀开处，棱CD是粘合处．请你想想，如何制作这个包装盒，然后完善下面的制作步骤．步骤1：在符合尺寸规格的硬纸板上，画出这个长方体的展开图(草图)．注意，要预留出黏合处，并适当剪去棱角．
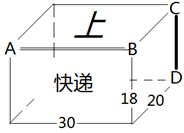
步骤2：在你上面画出的展开草图上，标出对应的A、B、C、D的位置，标出长30cm、宽20cm、高18CM所在线段，并把“上”和“快递”标注在所在面的位置上．
步骤3：裁下展开图，折叠并粘好黏合处，得到长方体包装盒．
9. 某“综合实践”小组开展了“长方体纸盒的制作”实践活动，他们利用边长为a（cm）的正方形纸板制作出两种不同方案的长方体盒子（图1为无盖的长方体纸盒，图2为有盖的长方体纸盒）．【操作一】根据图1方式制作一个无盖的长方体盒子．方法：先在纸板四角剪去四个同样大小边长为b（cm）的小正方形，再沿虚线折合起来．
(1)、【问题解决】若a＝12cm，b＝3cm，则长方体纸盒的底面积为 ；(2)、【操作二】根据图2方式制作一个有盖的长方体纸盒．方法：先在纸板四角剪去两个同样大小边长为b（cm）的小正方形和两个同样大小的小长方形，再沿虚线折合起来．
【拓展延伸】若a＝12cm，b＝2cm，该长方体纸盒的体积为 ；(3)、现有两张边长a均为30cm的正方形纸板，分别按图1、图2的要求制作无盖和有盖的两个长方体盒子，若b＝5cm，求无盖盒子的体积是有盖盒子体积的多少倍？10. 按要求完成下列视图问题， 其中小正方体的棱长为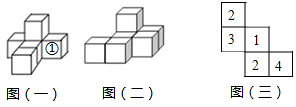
(1)、如图 一 ，它是由六个同样大小的正方体摆成的几何体 将正方体①移走后，新几何体的三视图与原几何体的三视图相比，哪一个视图没有发生改变？
(2)、如图 二 ，请你借助虚线网格 图四 画出该几何体的俯视图，该几何体的体积为.(3)、如图 三 ，它是由几个小立方块组成的俯视图，小正方形上的数字表示该位置上的正方体的个数，请你借助虚线网格 图五 画出该几何体的主视图.