【培优版】新北师大版(2024)数学七上1.1生活中的立体图形
试卷更新日期：2024-06-27 类型：同步测试
一、选择题
-
1. 下图左边的几何体可由（ ）图形绕虚线旋转而成.
A、
B、
C、
D、
2. 用一个平面分別去截下列几何体，截面不能得到圆的是（ ）A、
B、
C、
D、
3. 用一个平面去截一个正方体所得的截面的边数最多是（ ）A、4 B、3 C、6 D、54. 将自然数1至6分别写在一个正方体的6个面上，然后把任意相邻两个面上的数之和写在这两个面的公共棱上．则在这个正方体中所有棱上不同数的个数的最小值和最大值分别是（ ）A、7，9 B、6，9 C、7，10 D、3，115. 关于长方体有下列三个结论：
① 长方体中每一个面都是长方形；② 长方体中每两个面都互相垂直；
③ 长方体中相对的两个面是全等的长方形．
其中结论正确的个数有（ ）A、0个； B、1个； C、2个； D、3个.二、填空题
-
6. 在正方体、长方体、球、圆柱、圆锥、三棱柱这些几何体中，不属于柱体的有 ， 属于四棱柱的有 ．7. 从棱长为2的正方体毛坯的一角，挖去一个棱长为1的小正方体，得到一个如图所示的零件，则这个零件的表面积为 ．
8. 已知一个直棱柱共有15条棱，它的底面边长都是5cm，侧棱长都是4cm，则这个棱柱的所有侧面的面积之和是 ．9.如图所示，木工师傅把一个长为1.6米的长方体木料锯成3段后，表面积比原来增加了80cm2 ， 那么这根木料本来的体积是cm3 ．
10. 图中的大矩形长8厘米、宽6厘米，小矩形长4厘米、宽3厘米，以长边中点连线（图中的虚线）为轴，将图中的阴影部分旋转一周得到的几何体的表面积为平方厘米.
三、解答题
-
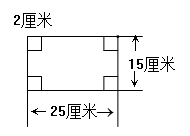
11. 一块长方形铁皮，长25厘米，宽15厘米，从四个角分别剪去边长2厘米的小正方形，然后把四周折起来，做成没有盖子的铁盒，铁盒的容积是多少升？
12.如图1是三个直立于水面上的形状完全相同的几何体（下底面为圆面，单位：厘米），将它们拼成如图2的新几何体，求该新几何体的体积（结果保留π）．
13. 如图所示，已知直角三角形纸板ABC，直角边AB=4 cm，BC=8 cm.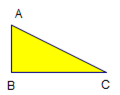
(1)、将直角三角形纸板ABC绕三角形的边所在的直线旋转一周，能得到种不同的几何体；(2)、分别计算绕三角形直角边所在的直线旋转一周，得到几何体的体积.（
取3） 14. 如图，如图几何体是由若干棱长为1的小立方体按一定规律在地面上摆成的，若将露出的表面都涂上颜色（底面不涂色），观察该图，探究其中的规律．
(1)、第1个几何体中只有2个面涂色的小立方体共有个．第3个几何体中只有2个面涂色的小立方体共有个．(2)、求出第100个几何体中只有2个面涂色的小立方体的块数．(3)、求出前100个几何体中只有2个面涂色的小立方体的块数的和．15. 如图，观察下列几何体并回答问题．
(1)、请观察所给几何体的面、棱、顶点的数量并归纳出棱柱有个面，条棱，个顶点；棱锥有个面，条棱，个顶点；(2)、所有像三棱柱、四棱柱、六棱柱、三棱锥等这样由四个或四个以上多边形所围成的立体图形叫做多面体，经过前人们归纳总结发现，多面体的面数 ， 顶点个数以及棱的条数存在着一定的关系，请根据（1）总结出这个关系为 ．