新人教版（2024版）七年级上学期数学课时进阶测试1.2有理数（三阶）

试卷更新日期：2024-06-27 类型：同步测试

进入出卷网下载

一、选择题

1. 已知： $m = \frac{| a + b |}{c} + \frac{2 | b + c |}{a} + \frac{3 | c + a |}{b}$ ，且 $a b c > 0$ ， $a + b + c = 0 .$ 则 $m$ 共有 $x$ 个不同的值，若在这些不同的 $m$ 值中，最大的值为 $y$ ，则 $x + y =$ （）

A、 $4$ B、 $3$ C、 $2$ D、 $1$

查看试题解析
2. 一电子跳蚤落在数轴上的某点k₀处，第一步从k₀向左跳一个单位到k₁ ，第二步从k₁向右跳2个单位到k₂ ，第三步由k₂处向左跳3个单位到k₃ ，第四步由k₃向右跳4个单位k₄ ， ….按以上规律跳了100步后，电子跳蚤落在数轴上的数是0，则k₀表示的数是

A、0 B、100 C、50 D、 $- 50$

查看试题解析
3. 若a≠0，b≠0，则代数式 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{a b}{| a b |}$ 的取值共有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 如图，圆的周长为4个单位长度．在该圆的4等分点处分别标上0、1、2、3，先让圆周上表示数字0的点与数轴上表示-1的点重合，再将数轴按逆时针方向环绕在该圆上．则数轴上表示2013的点与圆周上表示数字（）的点重合．

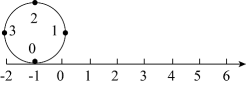A、0 B、1 C、2 D、3

查看试题解析
5. 数轴上表示整数的点称为整点，某数轴的单位长度为1cm ，若在数轴上画出一条长2020cm的线段AB ，则线段AB盖住的整点个数是（　　）

A、2020 B、2021 C、2020或2021 D、2019或2020

查看试题解析
6. 若a是有理数，那么在①a+1，②|a+1|，③|a|+1，④a²+1中，一定是正数的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 在数轴上表示有理数a ， ﹣a ， ﹣b－1的点如图所示，则（）

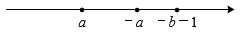A、﹣b＜﹣a B、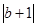＜ $| a |$ C、 $| a |$ ＞ D、b－1＜a

查看试题解析
8. 若a是负数，且|a|<1，则 $\frac{| a - 1 |}{| a | - 1}$ 的值是（）

A、等于1 B、大于-1，且小于0 C、小于-1 D、大于1

查看试题解析

二、填空题

9. 电影《哈利•波特》中，小哈利波特穿越墙进入“ $9 \frac{3}{4}$ 站台”的镜头（如示意图的Q站台），构思奇妙，能给观众留下深刻的印象．若A、B站台分别位于﹣ $\frac{2}{3}$ ， $\frac{8}{3}$ 处，AP=2PB，则P站台用类似电影的方法可称为“站台”．

查看试题解析
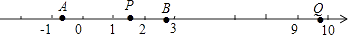10. 若 $| x | + 3 = | x - 3 |$ ，则x的取值范围是．

查看试题解析
11. 若 $n = \frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ ， $a b c > 0$ ，则n的值为．

查看试题解析
12. p、q、r、s在数轴上的位置如图所示：若|p－r|=10，|p－s|=12，|q－s|=9，则|q－r|的值为.

查看试题解析
13. 有理数a ， b ， c ， d满足 $\frac{| a b c d |}{a b c d} = - 1,$ 则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} + \frac{| d |}{d} =$ ．

查看试题解析
14.
点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，则在数轴上A、B两点之间的距离AB=|a﹣b|．
所以式子|x﹣2|的几何意义是数轴上表示x的点与表示2的点之间的距离．借助于数轴回答下列问题：
①数轴上表示2和5两点之间的距离是，数轴上表示1和﹣3的两点之间的距离是．
②数轴上表示x和﹣2的两点之间的距离表示为．
③数轴上表示x的点到表示1的点的距离与它到表示﹣3的点的距离之和可表示为：|x﹣1|+|x+3|．则|x﹣1|+|x+3|的最小值是．
④若|x﹣3|+|x+1|=8，则x=

查看试题解析

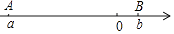
三、解答题

15. 在学习绝对值后，我们知道，|a|表示数a在数轴上的对应点与原点的距离．如：|5|表示5在数轴上的对应点到原点的距离．而|5|=|5﹣0|，即|5﹣0|表示5、0在数轴上对应的两点之间的距离．类似的，有：|5﹣3|表示5、3在数轴上对应的两点之间的距离；|5+3|=|5﹣（﹣3）|，所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离．一般地，点A、B在数轴上分别表示有理数a、b，那么A、B之间的距离可表示为|a﹣b|．
请根据绝对值的意义并结合数轴解答下列问题：

(1)、数轴上表示2和3的两点之间的距离是；数轴上P、Q两点的距离为3，点P表示的数是2，则点Q表示的数是．

(2)、点A、B、C在数轴上分别表示有理数x、﹣3、1，那么A到B的距离与A到C的距离之和可表示为（用含绝对值的式子表示）；满足|x﹣3|+|x+2|=7的x的值为．

(3)、试求|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣100|的最小值．

查看试题解析