人教版九年级上学期数学课时进阶测试22.2二次函数与一元二次方程(三阶)
试卷更新日期:2024-06-27 类型:同步测试
一、选择题
-
1. 在平面直角坐标系中,已知二次函数 , 其中 . 以下4个结论:
①若这个函数的图象经过点 , 则它必有最小值;
②若这个函数的图象经过第四象限的点 , 则必有;
③若 , 则方程必有一根小于 ,
④若 , 则当时,必有随的增大而增大.正确的是( )
A、①②③ B、②③ C、①③④ D、①②③④2. 关于一元二次方程有以下命题:①若a+b+c=0,则(≥0;②若方程(的两根为-1和2,则2a+c=0;③若方程(有两个不相等的实数根,则方程=0必有两个不相等的实数根;④若方程 有两个相等的实数根,则 无实数根.其中真命题是( )A、①② B、①②③ C、②③④ D、①③④3. 二次函数中,自变量与函数的对应值如下表:若 , 则下面叙述正确的是( )
A、该函数图象开口向上
B、该函数图象与轴的交点在轴的下方 C、对称轴是直线 D、若是方程的正数解,则4. 对于一个函数,自变量x取c时,函数值 等于0,则称c为这个函数的零点.若关于x的二次函数 有两个不相等的零点 ,关于x的方程 有两个不相等的非零实数根 ,则下列关系式一定正确的是( )A、 B、 C、 D、5. 已知函数f(x)=x2+2x , g(x)=2x2+6x+n2+3,当x=1时,f(1)=12+2×1=3,g(1)=2+6+n2+3=n2+11.则以下结论正确的有( )①若函数g(x)的顶点在x轴上,则;
②无论x取何值,总有g(x)>f(x);
③若﹣1≤x≤1时,g(x)+f(x)的最小值为7,则n=±3;
④当n=1时,令 , 则h(1)•h(2)…h(2023)=2024.
A、1个 B、2个 C、3个 D、4个二、填空题
-
6. 二次函数的大致图象如图所示,顶点坐标为 , 下列结论:
;
;
;
若方程有两个根和 , 且 , 则;
若方程有四个根,则这四个根的和为 .
其中正确的结论为 .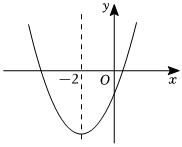 7. 如图,将二次函数(其中)的图象在轴下方的部分沿轴翻折,图象的其余部分保持不变,形成新的图象记为 , 另有一次函数的图象记为 , 若与恰有两个交点时,则的范围是.
7. 如图,将二次函数(其中)的图象在轴下方的部分沿轴翻折,图象的其余部分保持不变,形成新的图象记为 , 另有一次函数的图象记为 , 若与恰有两个交点时,则的范围是. 8. 已知二次函数 的图象经过点 与 ,关于 的方程 有两个根,其中一个根是5,若关于 的方程 有两个整数根,则这两个整数根分别是.9. 对于每个正整数 n , 关于 x 的一元二次方程 = 0 的两个根分别为 an、bn , 设平面直角坐标系中,An、Bn 两点的坐标分别为 An(an , 0),Bn(bn , 0),AnBn 表示这两点间的距离,则 AnBn=(用含 n 的代数式表示);A1B1+ A2B2+ …+ A2011B2012 的值为.
8. 已知二次函数 的图象经过点 与 ,关于 的方程 有两个根,其中一个根是5,若关于 的方程 有两个整数根,则这两个整数根分别是.9. 对于每个正整数 n , 关于 x 的一元二次方程 = 0 的两个根分别为 an、bn , 设平面直角坐标系中,An、Bn 两点的坐标分别为 An(an , 0),Bn(bn , 0),AnBn 表示这两点间的距离,则 AnBn=(用含 n 的代数式表示);A1B1+ A2B2+ …+ A2011B2012 的值为.三、解答题
-
10. 如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.
 (1)、求抛物线的解析式;(2)、过点A的直线交直线BC于点M.
(1)、求抛物线的解析式;(2)、过点A的直线交直线BC于点M.①当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,P,Q为顶点的四边形是平行四边形,求点P的横坐标;
②连接AC,当直线AM与直线BC的夹角等于∠ACB的2倍时,请直接写出点M的坐标.