人教版九年级上学期数学课时进阶测试22.1二次函数的图像和性质（二阶）

试卷更新日期：2024-06-27 类型：同步测试

进入出卷网下载

一、选择题

1. 抛物线 $y = a x^{2} + b x + c$ 的顶点为 $A (2 ， m)$ ，且经过点 $B (5 ， 0)$ ，其部分图象如图所示.对于此抛物线有如下四个结论：① $a c < 0$ ；② $a - b + c > 0$ ；③ $m + 9 a = 0$ ；④若此抛物线经过点 $C (t ， n)$ ，则 $t + 4$ 一定是方程 $a x^{2} + b x + c = n$ 的一个根．其中所有正确结论的序号是（）

A、①② B、①③ C、③④ D、①④

查看试题解析
2. 如图，在平面直角坐标系中，点A、E在抛物线 $y = a x^{2}$ 上，过点A、E分别作y轴的垂线，交抛物线于点B、F，分别过点E、F作x轴的垂线交线段AB于两点C、D．当点 $E (2 ， 4)$ ，四边形 $C D F E$ 为正方形时，则线段 $A B$ 的长为（　　）

A、4 B、 $4 \sqrt{2}$ C、5 D、 $5 \sqrt{2}$

查看试题解析
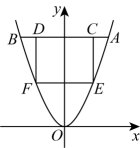3. 若无论 $x$ 取何值，代数式 $(x + 1 - 3 m) (x - m)$ 的值恒为非负数，则 $m$ 的值为（）

A、0 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、1

查看试题解析
4. 已知二次函数 $y = a x^{2} + b x - 1$ （a，b是常数， $a \neq 0$ ）的图象经过 $A (2 ， 1)$ ， $B (4 ， 3)$ ， $C (4 ， - 1)$ 三个点中的其中两个点.平移该函数的图象，使其顶点始终在直线 $y = x - 1$ 上，则平移后所得抛物线与y轴交点纵坐标的（）

A、最大值为-1 B、最小值为-1 C、最大值为 $- \frac{1}{2}$ D、最小值为 $- \frac{1}{2}$

查看试题解析
5. 已知二次函数y=-2x²+4x-3，如果y随x的增大而减小，那么x的取值范围是（）

A、x≥1 B、x≥0 C、x≥-1 D、x≥-2

查看试题解析
6. 下表中列出的是一个二次函数 $y = a x^{2} + b x + c$ 的自变量 $x$ 与函数 $y$ 的几组对应值：
$x$
…
$- 2$
0
1
3
…
$y$
…
6
$- 4$
$- 6$
$- 4$
…
下列各选项中，正确的是（）

A、这个函数的图象开口向下 B、当 $x > 1 ， y$ 的值随 $x$ 值的增大而增大 C、这个函数的最小值等于 $- 6$ D、一元二次方程 $a x^{2} + b x + c = 0$ 有一个实数根 $x$ 满足 $- 2 < x < 0$

查看试题解析

二、填空题

7. 已知一条抛物线的形状、开口方向均与抛物线y＝﹣2x²+9x相同，且它的顶点坐标为（﹣1，6），则这条抛物线的解析式为．

查看试题解析
8. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示抛物线的顶点坐标是 $(1, 1)$ ，有下列结论① $a > 0$ ；② $b^{2} - 4 a c > 0$ ；③ $4 a + b = 1$ ；④若点 $A (m, n)$ 在该抛物线上，则 $a m^{2} + b m + c \geq a + b + c$ ．其中正确的结论是．

查看试题解析
9. 二次函数y＝x²-2x+m与x轴的一个交点为（-1，0），则关于x的一元二次方程x²-2x+m=0的解为；

查看试题解析

三、解答题

10. 如图，在平面直角坐标系 $x O y$ 中，直线 $y = - \frac{1}{2} x + 2$ 与x轴交于点A，与y轴交于点B，抛物线 $y = - \frac{1}{2} x^{2} + b x + c$ 经过A，B两点且与x轴的负半轴交于点C．

(1)、求该抛物线的解析式．

(2)、若点D为直线 $A B$ 上方抛物线上的一个动点，当 $∠ A B D = 2 ∠ B A C$ 时，求点D的坐标．

(3)、已知E，F分别是直线 $A B$ 和抛物线上的动点，当 $E F ∥ O B$ ，且以B，O，E，F为顶点的四边形是平行四边形时，直接写出所有符合条件的E点的坐标．

查看试题解析
11. 某商家出售的一种商品成本价为 $20$ 元/千克，市场调查发现，该商品每天的销售量y（千克）与售价x（元/千克）满足一次函数 $y = - 2 x + 100$ ．设这种商品每天的销售利润为w元．

(1)、求w关于x的函数解析式；

(2)、该商品售价定为每千克多少元时，每天的销售利润最大？最大销售利润是多少？

查看试题解析

$x$	…	$- 2$	0	1	3	…
$y$	…	6	$- 4$	$- 6$	$- 4$	…