人教版九年级上学期数学课时进阶测试21.3实际问题与一元二次方程（二阶）

试卷更新日期：2024-06-26 类型：同步测试

进入出卷网下载

一、选择题

1. 小明同学是一位古诗文的爱好者，在学习了一元二次方程这一章后，改编了苏轼诗词《念奴娇·赤壁怀古》：“大江东去浪淘尽，千古风流人物．而立之年督东吴，早逝英年两位数．十位恰小个位三，个位平方与寿同．哪位学子算得快，多少年华数周瑜？”假设周瑜去世时年龄的十位数字是 $x$ ，则可列方程为（）

A、 $10 x + (x - 3) = {(x - 3)}^{2}$ B、 $10 (x + 3) + x = x^{2}$ C、 $10 x + (x + 3) = {(x + 3)}^{2}$ D、 $10 (x + 3) + x = {(x + 3)}^{2}$

查看试题解析
2. 某电影院所有大厅可容纳的人数相同，所有小厅可容纳的人数也相同。2个大厅和1个小厅共可同时容纳1960人观影；1个大厅和2个小厅共可同时容纳1460人观影．如果设一个大厅可同时容纳y人观影，由题意列出的方程正确的是（）

A、 $y + \frac{1}{2} (1960 - y) = 1460$ B、 $y + 2 (1460 - y) = 1960$ C、 $2 y + 2 (1460 - y) = 1960$ D、 $y + 2 (1960 - 2 y) = 1460$

查看试题解析
3. 如图， $R t △ A C B$ 中， $∠ C = 90 ° ， A C = 7 ， B C = 5$ ，点P从点B出发向终点C以1个单位长度/s移动，点Q从点C出发向终点A以2个单位长度/s移动，P ， Q两点同时出发，任意一点先到达终点时，两点同时停止，当 $△ P C Q$ 的面积等于4时，则P ， Q两点同时移动的时间是（）

A、1秒或4秒 B、1秒 C、2秒或4秒 D、4秒

查看试题解析
4. 某公司今年4月的营业额为2500万元，按计划第二季度的总营业额要达到9100万元，设该公司5、6两月的营业额的月平均增长率为x．根据题意列方程，则下列方程正确的是（）

A、 $2500 {(1 + x)}^{2} ＝ 9100$ B、 $2500 {(1 + x %)}^{2} ＝ 9100$ C、 $2500 (1 + x) + 2500 {(1 + x)}^{2} ＝ 9100$ D、 $2500 + 2500 (1 + x) + 2500 {(1 + x)}^{2} ＝ 9100$

查看试题解析
5.
如图，在一幅长为60cm，宽为40cm的矩形风景画的四周镶一条相同宽度的纸边，制成一幅矩形挂图．若要使整个挂图的面积是3500cm² ，设纸边的宽为x（cm），则x满足的方程是（）

A、（60+x）（40+x）=3500 B、（60+2x）（40+2x）=3500 C、（60﹣x）（40﹣x）=3500 D、（60﹣2x）（40﹣2x）=3500

查看试题解析
6. 从前有一个醉汉拿着竹竿进城，横拿竖拿都进不去，横着比城门宽 $\frac{4}{3}$ 米，竖着比城门高 $\frac{2}{3}$ 米，一个聪明人告诉他沿着城门的两对角斜着拿竿，这个醉汉一试，不多不少刚好进去了，求竹竿的长度.若设竹竿长x米，则根据题意，可列方程（　　）

A、 ${(x + \frac{4}{3})}^{2} + {(x + \frac{2}{3})}^{2} = x^{2}$ B、 ${(x - \frac{4}{3})}^{2} + {(x - \frac{2}{3})}^{2} = x^{2}$ C、 ${(x - \frac{4}{3})}^{2} + {(x + \frac{2}{3})}^{2} = x^{2}$ D、 ${(x + \frac{4}{3})}^{2} + {(x - \frac{2}{3})}^{2} = x^{2}$

查看试题解析
7. 某校组织学生到一片荒地上进行植树活动，原计划植树8行10列，后来增加了40棵树，为了美观起见，要求增加的行数、列数相同，设增加了x行，根据题意，所列方程正确的是（）

A、 $(8 - x) (10 - x) = 8 \times 10 - 40$ B、 $(8 - x) (10 - x) = 8 \times 10 + 40$ C、 $(8 + x) (10 + x) = 8 \times 10 - 40$ D、 $(8 + x) (10 + x) = 8 \times 10 + 40$

查看试题解析
8. 某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（）

A、560(1＋x)²＝315 B、560(1－x)²＝315 C、560(1－2x)²＝315 D、560(1－x²)＝315

查看试题解析

二、填空题

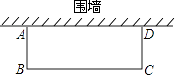
9. 某玩具商店出售一种“小猪佩奇”玩具，平均每天可销售50个，每个盈利36元，为了尽快减少库存，商场决定采取适当的降价措施，调查发现，若每个玩具降价1元，平均每天可多售出5个，商店要想平均每天销售这种玩具盈利2400元，则每个玩具应降价多少元？设每个玩具应降价x元，可列方程为．

查看试题解析
10. 一个两位数，十位上的数字比个位上的数字的平方少9.如果把十位上的数字与个位上的数字对调，得到的两位数比原来的两位数小27，则原来的两位数是

查看试题解析
11. 对于两个不相等的实数 $a$ 、 $b$ ，我们规定符号 $M a x {a ， b}$ 表示 $a$ 、 $b$ 中的较大值，如： $M a x {1 ， 3} = 3$ ，按照这个规定，方程 $M a x {1 ， x} = x^{2} - 6$ 的解为．

查看试题解析
12. 如图，邻边不等的矩形花圃ABCD，它的一边AD利用已有的围墙，另外三边所围的栅栏的总长度是6m．若矩形的面积为4m² ，则AB的长度是 m（可利用的围墙长度超过6m）．

查看试题解析
13. 某航空公司有若干个飞机场，每两个飞机场之间都开辟一条航线，一共开辟了28条航线，则这个航空公司共有个飞机场.．

查看试题解析

三、解答题

14. 列方程解应用题：
某玩具厂生产一种玩具，按照控制固定成本降价促销的原则，使生产的玩具能够及时售出，据市场调查：每个玩具按480元销售时，每天可销售160个；若销售单价每降低1元，每天可多售出2个，已知每个玩具的固定成本为360元，问这种玩具的销售单价为多少元时，厂家每天可获利润20000元？

查看试题解析
15. 某果农计划在一片向阳的坡地上种植100棵桃树，果农想通过增加种植桃树的数量来增加产量，但他发现多种20棵桃树，则每亩地多种4棵．

(1)、求果农原计划每亩地种多少棵桃树？

(2)、果农经过咨询专业技术人员，发现按原计划种树，每棵桃树在生产周期内的平均产量是1000个桃子，若多种1棵桃树，每棵桃树在生产周期内的平均产量就会减少2个桃子，而且多种的桃树不能超过100棵．如果要使产量增加15.2%，那么应多种多少棵桃树？

查看试题解析