广东省惠州市惠城区2024年九年级数学学业水平考试

试卷更新日期：2024-06-25 类型：中考模拟

进入出卷网下载

一、选择题：本大题共10个小题，每小题3分，共30分．在每个小题给出的四个选项中，只有一项符合题目要求的.

1. -4的相反数是（）

A、 $\frac{1}{4}$ B、 $- \frac{1}{4}$ C、4 D、-4

查看试题解析
2. 下列图形中，既是中心对称图形又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 赤道长约为40 000 000m，用科学记数法可以把数字40 000 000表示为（）

A、4×10⁷ B、40×10⁶ C、400×10⁵ D、4000×10³

查看试题解析
4. 如图， $l_{1} ∥ l_{2}$ ， $∠ 1 = 35 °$ ， $∠ 2 = 50 °$ ，则 $∠ 3$ 的度数为（）

A、 $35^{°}$ B、 $50^{°}$ C、 $85^{°}$ D、 $95^{°}$

查看试题解析
5. 某校为庆祝中国共产党建党100周年举行“传承红色基因，沐浴阳光成长”歌咏比赛，七年级8个班通过抽签决定出场顺序，七年级（1）班恰好抽到第1个出场的概率为（）

A、 $\frac{1}{10}$ B、 $\frac{1}{8}$ C、 $\frac{8}{10}$ D、 $\frac{1}{4}$

查看试题解析
6. 如图，在Rt△ABC中，∠C＝90°，AC＝5，BC＝12．若D ， E分别为边AC ， BC的中点，则DE的长为（　　）

A、5 B、5.5 C、6 D、6.5

查看试题解析
7. 不等式组 ${\begin{matrix} 2 x \geq - 2 \\ x + 3 < 4 \end{matrix}$ 的解在数轴上表示为（）

A、 B、 C、 D、

查看试题解析
8. 设方程 $x^{2} - 3 x + 2 = 0$ 的两根分别是 $x_{1} ， x_{2}$ ，则 $x_{1} + x_{2}$ 是（）．

A、-3 B、-2 C、2 D、3

查看试题解析
9. 某服装的进价为400元，出售时标价为600元，由于换季，商场准备打折销售，但要保证利润率不低于20%，那么该服装至多打（）折．

A、7 B、 $7$ .5 C、8 D、8.5

查看试题解析
10. 如图，四边形 $A B C D$ 内接于 $⊙ O ， D E$ 是 $⊙ O$ 的直径，连接 $B D$ ，若 $∠ B C D = 120 °$ ，则 $∠ B D E$ 的度数是（）

A、 $25 °$ B、 $30 °$ C、 $32 °$ D、 $35 °$

查看试题解析

二、填空题：本大题共5个小题，每小题3分，共15分.

11. 计算： $\sqrt{2} + 2 \sqrt{2} =$ ．

查看试题解析
12. 某仓库运进小麦6吨，记为+6吨，那么仓库运出小麦8吨应记为吨．．

查看试题解析
13. 已知反比例函数y $= \frac{k}{x}$ 的图象经过点（﹣3，4），则k的值为．

查看试题解析
14. 已知圆锥的底面半径为 $4 c m$ ，母线长为 $6 c m$ ，则圆锥的侧面积为 $c m^{2}$ ．

查看试题解析
15. 如图，四边形 $A B C D$ 是边长为2的正方形，点 $P$ 在正方形 $A B C D$ 内， $△ P B C$ 是等边三角形，则 $△ P B D$ 的面积为．

查看试题解析

三、解答题（一）：本大题共5小题，每小题5分，共25分.

16. 计算： $4 s i n 60 ° - \sqrt{12} + (\sqrt{3} - 1)^{0}$ .

查看试题解析
17. 先化简，再求值：( $\frac{x}{x - 3} + \frac{1}{x - 3}$ )× $\frac{x^{2} - 9}{x + 1}$ ，其中 $x = 2$ ．

查看试题解析
18. 如图，AB=CB，BE=BF，∠1=∠2，证明：△ABE≌△CBF．

查看试题解析
19. 2022年4月16日，神舟十三号载人飞船返回舱成功着陆，任务取得圆满成功．航模店看准商机，同样花费320元，购进“天宫”模型的数量比“神舟”模型多4个且每个“天宫”模型成本比每个“神舟”模型成本少 $20 %$ ． “神舟”和“天宫”模型的成本各多少元？

查看试题解析
20. 某县消防大队到某小区进行消防演习.已知，图 $1$ 是一辆登高云梯消防车的实物图，图 $2$ 是其工作示意图，起重臂 $A C$ 可伸缩 $(15 m \leq A C \leq 26 m)$ ，且起重臂 $A C$ 可绕点 $A$ 在一定范围内转动，张角为 $∠ C A E (90 ° ≤ ∠ C A E ≤ 150 °)$ 转动点A距离地面 $B D$ 的高度 $A E$ 为 $3 m$ ．当起重臂 $A C$ 长度为 $20 m$ ，张角 $∠ C A E = 127 °$ ，求云梯消防车最高点 $C$ 距离地面 $B D$ 的高度 $C F$ .（参考数据： $s i n 37 ° \approx 0.60$ ， $c o s 37 ° \approx 0.80$ ， $t a n 37 ° \approx 0.75$ ， $\sqrt{3} \approx 1.73$ ）

查看试题解析

四、解答题（二）：本大题共3小题，第21题8分，第22、23题各9分，共26分.

21. 如图，线段AD是△ABC的角平分线.

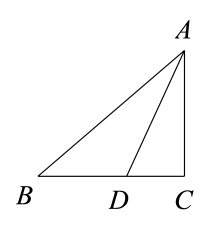(1)、尺规作图：作线段AD的垂直平分线分别交AB，AC于点E，F：（保留痕迹，不写作法）

(2)、在（1）所作的图中，连接DE，DF，求证：四边形AEDF是菱形.

查看试题解析
22. 问题情景：九（1）班综合实践小组进行废物再利用的环保小卫士行动，他们准备用废弃的宣传单制作装垃圾用的无盖纸盒．
操作探究：

(1)、若准备制作一个无盖的正方体纸盒，图1中的图形经过折叠能围成无盖正方体纸盒；

(2)、图2是小明的设计图，把它折成无盖正方体纸盒后，与“卫”字相对的是；

(3)、如图3，有一张边长为20cm的正方形废弃宣传单，小华准备将其四角各剪去一个小正方形，折成无盖长方体纸盒．
①请你在图3中画出示意图，用实线表示剪切线，虚线表示折痕；
②若四角各剪去了一个边长为3cm的小正方形，求这个纸盒的容积．

查看试题解析
23. 某校260名学生参加植树活动，要求每人植4～7棵，活动结束后随机抽查了若干名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；C：7棵；将各类的人数绘制成扇形图(如图1)和条形图(如图2).回答下列问题：

(1)、在这次调查中D类型有多少名学生？(并在图中画出)

(2)、写出被调查学生每人植树量的众数、中位数；

(3)、求被调查学生每人植树量的平均数，并估计这260名学生共植树多少棵？

查看试题解析

五、解答题（三）：本大题共2小题，每小题12分，共24分.

24. 如图，抛物线y＝﹣x²+bx+c与x轴交于A、B两点（A在B的左侧），与y轴交于点N，过A点的直线l：y＝kx+n与y轴交于点C，与抛物线y＝﹣x²+bx+c的另一个交点为D，已知A（﹣1，0），D（5，﹣6），P点为抛物线y＝﹣x²+bx+c上一动点（不与A、D重合）．

(1)、求抛物线和直线l的解析式；

(2)、当点P在直线l上方的抛物线上时，连接PA、PD，当△PAD的面积最大时，求P点的坐标.

(3)、设M为直线l上的点，探究是否存在点M，使得以点N、C、M、P为顶点的四边形为平行四边形？若存在，直接写出点M的坐标；若不存在，请说明理由。

查看试题解析
25.
问题情境：数学活动课上，老师出示了一个问题：如图①，在▱ABCD中，BE⊥AD ，垂足为E ， F为CD的中点，连接EF ， BF ，试猜想EF与BF的数量关系，并加以证明．

(1)、独立思考：请解答老师提出的问题；

(2)、实践探究：希望小组受此问题的启发，将▱ABCD沿着BF（F为CD的中点）所在直线折叠，如图②，点C的对应点为C^' ，连接DC^'并延长交AB于点G ，请判断AG与BG的数量关系，并加以证明．

(3)、问题解决：智慧小组突发奇想，将▱ABCD沿过点B的直线折叠，如图③，点A的对应点为A^' ，使A^'B⊥CD于点H ，折痕交AD于点M ，连接A^'M ，交CD于点N ．该小组提出一个问题：若此▱ABCD的面积为20，边长AB＝5，BC＝2 $\sqrt{5}$ ，求图中阴影部分（四边形BHNM）的面积．请你思考此问题，直接写出结果．

查看试题解析