安徽省滁州市定远县重点中学2017-2018学年高一上学期数学期中考试试卷

试卷更新日期：2017-12-04 类型：期中考试

进入出卷网下载

一、单项选择题

1. 下列各式中，表示y是x的函数的有（）
①y=x﹣（x﹣3）；
②y= $\sqrt{x - 2}$ + $\sqrt{1 - x}$ ；
③y= ${\begin{matrix} x - 1 (x < 0) \\ x + 1 (x \geq 0) \end{matrix}$
④y= ${\begin{matrix} 0 (x 为有理数) \\ 1 (x 为实数) . \end{matrix}$ ．

A、4个 B、3个 C、2个 D、1个

查看试题解析
2. 若函数y=f（x）的定义域为M={x|﹣2≤x≤2}，值域为N={y|0≤y≤2}，则函数y=f（x）的图象可能是（）

A、 B、 C、 D、

查看试题解析
3. 函数f（x）= $\frac{\sqrt{4 - x}}{x - 3}$ 的定义域为（）

A、（﹣∞，4] B、（﹣∞，3）∪（3，4] C、[﹣2，2] D、（﹣1，2]

查看试题解析
4. 若函数y=f（x）的定义域是[0，2]，则函数y=f（2x﹣1）的定义域是（）

A、{x|0≤x≤1} B、{x|0≤x≤2} C、{x| $\frac{1}{2}$ ≤x≤ $\frac{3}{2}$ } D、{x|﹣1≤x≤3}

查看试题解析
5. 设全集为R，函数f（x）= $\sqrt{1 - x}$ 的定义域为M，则∁_RM为（）

A、{x|x＜1} B、{x|x＞1} C、{x|x≤1} D、{x|x≥1}

查看试题解析
6. 函数y=x²﹣4x+3，x∈[0，3]的值域为（）

A、[0，3] B、[﹣1，0] C、[﹣1，3] D、[0，2]

查看试题解析
7. 下列各组函数表示同一函数的是（）

A、 $f (x) = \sqrt{x^{2}} ， g (x) = {(\sqrt{x})}^{2}$ B、f（x）=1，g（x）=x⁰ C、 $f (x) = {\begin{matrix} x (x \geq 0) \\ - x (x < 0) \end{matrix} ， g (t) = | t |$ D、 $f (x) = x + 1 ， g (x) = \frac{x^{2} - 1}{x - 1}$

查看试题解析
8. 一次函数g（x）满足g[g（x）]=9x+8，则g（x）是（）

A、g（x）=9x+8 B、g（x）=3x+8 C、g（x）=﹣3x﹣4 D、g（x）=3x+2或g（x）=﹣3x﹣4

查看试题解析
9. 已知函数f（x）在R上是增函数，则下列说法正确的是（）

A、y=﹣f（x）在R上是减函数 B、y= $\frac{1}{f (x)}$ 在R上是减函数 C、y=[f（x）]²在R上是增函数 D、y=af（x）（a为实数）在R上是增函数

查看试题解析
10. 设 $f (x) = {\begin{matrix} x^{2} ， x < 0 \\ 2^{x} ， x \geq 0 \end{matrix}$ ，则f[f（﹣1）]=（）

A、1 B、2 C、4 D、8

查看试题解析
11. 已知函数f（x）=4+a^x⁺¹的图象恒过定点P，则点P的坐标是（）

A、（﹣1，5） B、（﹣1，4） C、（0，4） D、（4，0）

查看试题解析
12. 已知函数f（x）是奇函数，且在（﹣∞，+∞）上为增函数，若x，y满足等式f（2x²﹣4x）+f（y）=0，则4x+y的最大值是（）

A、10 B、﹣6 C、8 D、9

查看试题解析

二、填空题

13. 函数y=﹣ $\frac{2}{x + 1}$ 的定义域是[0，2]，则其值域是．

查看试题解析
14. 若函数f（x）的定义域为[2a﹣1，a+1]，值域为[a+3，4a]，则a的取值范围为．

查看试题解析
15. 已知f（2x+1）=4x²+4x+3，则f（1）= ．

查看试题解析
16. 若x₁、x₂为方程2^x= ${(\frac{1}{2})}^{- \frac{1}{x} + 1}$ 的两个实数解，则x₁+x₂= ．

查看试题解析

三、解答题

17. 已知f（x）= $\frac{1}{1 + x}$ （x∈R，且x≠﹣1），g（x）=x²+2（x∈R）．

(1)、求f（2），g（2）的值；

(2)、求f（g（2）），g（f（2））的值；

(3)、求f（g（x））．

查看试题解析
18. 如图所示，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4）．

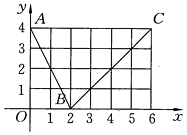(1)、求f[f（0）]的值；

(2)、求函数f（x）的解析式．

查看试题解析
19. 计算下列各式的值：

(1)、（ln 5）⁰+^（ $\frac{9}{4}$ ）^0.5+ $\sqrt{{(1 - \sqrt{2})}^{2}}$ ﹣2^log₄²；

(2)、log₂1﹣lg 3•log₃2﹣lg 5．

查看试题解析
20. 已知函数 $f (x) = \frac{3^{x} - 2^{- x}}{3^{x} + 2^{- x}}$ ．
（1）判断f（x）的奇偶性；

（2）判断f（x）的单调性，并加以证明；

（3）写出f（x）的值域．

查看试题解析
21. 已知函数f（x）是定义域为R的偶函数，当x≥0时，f（x）= $\frac{x}{1 + x}$ ．

(1)、求x＜0时，f（x）的解析式；

(2)、画出函数f（x）在R上的图象；

(3)、结合图象写出f（x）的值域．

查看试题解析
22. 函数f（x）的定义域为D={x|x≠0}，且满足对于任意x₁ ， x₂∈D，有f（x₁•x₂）=f（x₁）+f（x₂）．

(1)、求f（1）的值；

(2)、判断f（x）的奇偶性并证明你的结论；

(3)、如果f（4）=1，f（x﹣1）＜2，且f（x）在（0，+∞）上是增函数，求x的取值范围．

查看试题解析