江西省抚州市临川区2024年中考数学一模试题-在线组卷题库

1. 3的相反数的绝对值是（）

A、3 B、 $\frac{1}{3}$ C、 $- \frac{1}{3}$ D、 $- 3$

查看试题解析
2. 下列计算正硧的是（）

A、 $1^{2} \cdot m^{3} = n^{6}$ B、 ${(2 m^{2})}^{3} = 8 m^{6}$ C、 $(m + 1)^{2} = m^{2} + 1$ D、 $(m^{3} + m) \div m = m^{2}$

查看试题解析
3. 已知关于 $x$ 的一元二次方程 $m x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则 $m$ 的取值范围是（）

A、 $m t < - 1$ B、 $m > 1$ C、 $m < 1$ 且 $m \neq 0$ D、 $m > - 1$ 且 $m \neq 0$

查看试题解析
4. 小明在测量楼高时，先测出楼房落在地面上的影长BA为15米（如图），然后在A处树立一根高2米的标杆，测得标杆的影长AC为3米，则楼高为（　　）

A、10米 B、12米 C、15米 D、22.5米

查看试题解析
5. 如图，直线 $l_{1} ∥ l_{2}$ ，点 $C 、 A$ 分别在 $l_{1} 、 l_{2}$ 上，以点 $A$ 为圆心，适当长为半径画弧，交 $A C 、 l_{2}$ 于点 $D 、 E;$ 分别以 $D 、 E$ 为圆心，大于 $\frac{1}{2} D E$ 长为半径画弧，两弧交于点 $F$ ；作射线 $A F$ 交 $l_{1}$ 于点．B．若 $∠ B C A = 120 °$ ，则 $∠ 1$ 的度数为（）

A、 $20 °$ B、 $25 °$ C、 $30 °$ D、 $50 °$

查看试题解析
6. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的部分图象如图所示，图象过点 $(- 1 ， 0)$ ，对称轴为直线 $x = 1$ ，则有下列结论：① $a b c < 0$ ；② $b < c$ ；③ $3 a + c = 0$ ；④对于任意实数 $m$ ， $a + b \geq a m^{2} + b m$ ；其中结论正确的个数为（）

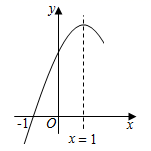A、1个 B、2个 C、3个 D、4个

查看试题解析

7. 因式分解： $a^{2} - 4$ =.

查看试题解析
8. 在平面直角坐标系中，点 $P (3 ， - 4)$ 关于原点对称的点的坐标是．

查看试题解析
9. 已知方程 $x^{2} - 2 x - 8 = 0$ 的两根分别是 $x_{1}$ 和 $x_{2}$ ，那么 $x_{1} + x_{2} - x_{1} x_{2}$ 的值为．

查看试题解析
10. 如图， $F$ 是矩形 $A B C D$ 的边 $C D$ 上一点，射线 $B F$ 交 $A D$ 的延长线于点 $E$ ，已知 $D E = 2 B C, C D = 6$ ，则 $C F$ 的长为．

查看试题解析
11. 如图，从一个半径为1的圆形铁皮中剪出一个圆心角为 $90 °$ 的扇形，并将剪下来的扇形围成一个圆锥，则此圆锥的底面圆的半径是．

查看试题解析
12. 如图， $△ A B C$ 中， $A B = A C, ∠ A = 30 °$ ，射线 $C P$ 从射线 $C A$ 开始绕点 $C$ 逆时针旋转 $α$ 角 $(0 ° < α < 75 °)$ ，与射线 $A B$ 相交于点 $D$ ，将 $△ A C D$ 沿射线 $C P$ 翻折至 $△ A^{'} C D$ 处，射线 $C A^{'}$ 与射线 $A B$ 相交于点 $E$ ．若 $△ A^{'} D E$ 是等腰三角形，则 $∠ α$ 的度数为．

查看试题解析

13.

(1)、解不等式组： ${\begin{array}{l} 2 x - 6 \leq 0 \\ \frac{x - 1}{2} < x \end{array}$ ．

(2)、先化简 $(\frac{a}{a^{2} - 4} + \frac{1}{2 - a}) \div \frac{2 a + 4}{a^{2} + 4 a + 4}$ ，再求值，其中 $a = \sqrt{3} + 2$ ．

查看试题解析
14. 如图，在正方形 $A B C D$ 中， $A B = 4, E$ 为 $A B$ 的中点，连接 $D E$ ，将 $△ D A E$ 绕点 $D$ 按逆时针方向旋转 $90 °$ 得到 $△ D C F$ ，连接 $E F$ ，求 $E F$ 的长．

查看试题解析
15. 如图，已知正六边形 $A B C D E F$ ，请仅用无刻度的直尺按要求完成以下作图（保留作图痕迹）．

(1)、在图1的正六边形 $A B C D E F$ 内部作一点 $M$ ，连接 $A M$ ，使得 $s i n ∠ B A M = \frac{\sqrt{3}}{2}$ ．

(2)、在图2的正六边形 $A B C D E F$ 内部作一点 $N$ ，连接 $A N$ ，使得 $t a n ∠ B A N = \frac{\sqrt{3}}{2}$ ．

查看试题解析
16. “抚州是个有梦有戏的好地方”这是江西抚州文旅的宣传标语，小强、小红准备采用抽签的方式，各自随机选取江西抚州四个景点（A．文昌里；B．三翁花园；C．名人雕塑园；D．仙盖山）中的一个景点游玩，四支签分别标有A，B，C，D．

(1)、小强抽一次签，他恰好抽到A景区是事件．（填“必然”“不可能”或“随机”）

(2)、若规定其中一人抽完签后，放回，下一个人再抽，请用列表或树状图的方法，求小强、小红抽到同一景点的概率．

查看试题解析
17. 如图，已知直线 $l$ 交 $x$ 轴， $y$ 轴于 $A, B$ 两点，动点 $P (x, y)$ 在直线 $l$ 上，且满足： $x + y = 10$ ．

(1)、直接写出直线 $l$ 的解析式为：；

(2)、若反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象与直线 $A B$ 相交于 $C 、 D$ 两点，连接 $O C, O D$ ，已知点 $C$ 的横坐标为8，求 $△ O C D$ 的面积．

查看试题解析

18. 为响应国家节能减排的倡议，某汽车专卖店销售A，B两种型号的新能源汽车，B型汽车的售价比A型汽车售价高8万元，本周售出1辆A型车和3辆B型车，销售总额为96万元．

(1)、求每辆A型车和B型车的售价；

(2)、随着新能源汽车越来越受消费者认可，汽车专卖店计划下周销售A，B两种型号的汽车共10辆，若销售总额不少于228万元，求B型车至少销售多少辆？

查看试题解析
19. 如图1，一个纸筒被安装在竖直的墙面上，图2是其侧面示意图，其中 $A B ⊥ B C$ ， $A B ∥ C E ∥ D F, A D ∥ E F ∥ B C$ ，纸筒盖 $C M P$ 可以绕着点 $C$ 旋转，关闭时点 $P$ 与点 $F$ 重合， $C M ⊥ P M, A B = 30 c m, D F = 6 c m, C M = E F = 7 c m$ ．（结果保留整数．参考数据： $s i n 11.5 ° \approx 0.20, c o s 11.5 ° \approx 0.98, t a n 11.5 ° \approx 0.20$ ）

(1)、若 $∠ B C M = 150 °$ ，求纸筒盖关闭时点 $P$ 运动的路径长．

(2)、当一卷底面直径为 $10 c m$ 的圆柱形纸巾能放入纸筒内时（即打开时点 $P$ 与点 $F$ 两点之间距离不小于 $10 c m$ ），问纸筒盖CMP打开的最小角的度数．

查看试题解析
20.

(1)、如图， $A B$ 是 $⊙ O$ 的直径， $A C$ 与 $⊙ O$ 交于点 $F$ ，弦 $A D$ 平分 $∠ B A C$ ，点 $E$ 在 $A C$ 上，连接 $D E, D B$ ， ▲ ．求证： ▲ ．
从① $D E$ 与 $⊙ O$ 相切；② $D E ⊥ A C$ ；中选择一个作为已知条件，余下的一个作为结论，将题目补充完整（填写序号），并完成证明过程．

(2)、在（1）的前提下，若 $A B = 6, ∠ B A D = 30 °$ ，求 $E F$ 的长．

查看试题解析

21. 为弘扬学生爱国主义教育，某校在清明节来临之际开展“走进清明·缅怀英烈”知识竞赛活动，现从九年级和八年段参加活动的学生中各随机抽取20名同学的成绩进行整理、描述和分析（成绩用x表示，共分为四组：A． $x < 70$ ， B． $70 \leq x < 80$ ， C． $80 \leq x < 90$ ， D． $90 \leq x \leq 100$ ，下面给出了部分信息：
九年级学生成绩为：66，76，77，78，79，81，82，83，84，86，86，86，88，88，91，91，92，95，96，99；
八年级C组学生成绩为：88，81，84，86，87，83，89．
九、八年级学生成绩统计表：
年级
平均数
中位数
众数
方差
九年级
85.2
86
b
62.1
八年级
85.2
a
91
55.3
根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ， $m =$ ；

(2)、根据以上数据，你认为哪个年级对爱国主义教育知识掌握更好？请说明理由（写出一条理由即可）；

(3)、该校九、八年级共640名学生参加了此次知识竞赛活动，估计两个年级成绩为优秀（90分及以上）的学生共有多少人？

查看试题解析
22. 某数学小组在一次数学探究活动过程中，经历了如下过程：
问题提出：如图，正方形 $A B C D$ 中， $A B = 8, P$ 为对角线 $A C$ 上的一个动点，以P为直角顶点，向右作等腰直角 $△ D P M$ ．

(1)、操作发现： $D M$ 的最小值为，最大值为；

(2)、数学思考：求证：点 $M$ 在射线 $B C$ 上；

(3)、拓展应用：当 $C P = C M$ 时，求 $C M$ 的长．

查看试题解析

23. 定义：若直线 $y = - 1$ 与开口向下的拋物线有两个交点，则这两个交点之间的距离叫做这条抛物线的“反碟长”．如图，已知拋物线 $L_{1} : y = - x^{2}$ 与直线 $y = - 1$ 相交于 $P, Q$ ．

(1)、抛物线 $L_{1}$ 的“反碟长” $P Q =$ ．

(2)、拋物线随其顶点沿直线 $y = \frac{1}{2} x$ 向上平移，得到拋物线 $L_{2}$ ．
①当抛物线 $L_{1}$ 的顶点平移到点 $(6, 3)$ ，抛物线 $L_{2}$ 的解析式是 ▲ ．抛物线 $L_{2}$ 的“反碟长”是 ▲ ．
②若抛物线 $L_{2}$ 的“反碟长”是一个偶数，则其顶点的纵坐标可能是 ▲ ．（填写所有正确的选项）
A.15 B.16 C.24 D.25
③当抛物线 $L_{2}$ 的顶点 $A$ 和拋物线 $L_{2}$ 与直线 $y = - 1$ 的两个交点 $B$ ， $C$ 构成一个等边三角形时（点 $B$ 在点 $C$ 左边），求点 $A$ 的坐标．

查看试题解析

江西省抚州市临川区2024年中考数学一模试题

一、选择题（本大题共6个小题，每小题3分，共18分）每小题只有一个正确选项．

二、填空题（本大题共8个小题，每小题3分，共24分）

三、（本大题共5个小题，每小题6分，共30分）

四、（本大题共3个小题，每小题8分，共24分）

五、（本大题共2个小题，每小题9分，共18分）

六、（本大题共12分）

年级	平均数	中位数	众数	方差
九年级	85.2	86	b	62.1
八年级	85.2	a	91	55.3