湖南省岳阳市汨罗市2023-2024学年九年级下学期学习能力检测竞赛数学试题

试卷更新日期：2024-06-17 类型：竞赛测试

进入出卷网下载

一、单选题（本题共8小题，每小题2分，共16分）

1. 如图，在等腰直角三角形ABC中，∠C＝90°，AC＝6，D是AC上一点，若tan∠DBA＝ $\frac{1}{5}$ ，则sin∠CBD的值为（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2 \sqrt{13}}{13}$ D、 $\frac{3 \sqrt{13}}{13}$

查看试题解析
2. 下列命题中，表述正确的是（）

A、对角线互相垂直且相等的四边形是正方形 B、方程2x²﹣3x﹣2＝0有两个相等的实数根 C、反比例函数y＝ $\frac{k}{x}$ 的图象经过点（﹣2，﹣1），则其函数值y随x的增大而增大 D、点C是线段AB上的一点，若AC²＝AB•BC ，则称点C是AB的黄金分割点．若线段AB＝ $\sqrt{5}$ ， C是AB的黄金分割点，且AC＞BC ，则AC＝ $\frac{5 - \sqrt{5}}{2}$

查看试题解析
3. 如图，在 $△ A B C$ 中， $∠ B = 45 °$ ， $∠ C = 60 °$ ， $A D ⊥ B C$ 于点 $D$ ， $B D = \sqrt{6}$ ，若 $E$ ， $F$ 分别为 $A B$ ， $B C$ 的中点，则 $E F$ 的长为（）

A、 $\sqrt{2}$ B、 $\frac{\sqrt{6}}{2}$ C、 $\frac{\sqrt{6}}{3}$ D、 $\sqrt{3}$

查看试题解析
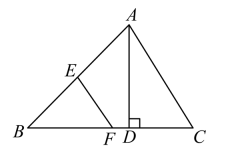4. 如图，在长方形ABCD中，E为AB中点，以BE为边作正方形BEFG ，边EF交CD于点H ，在边BE上取点M使BM＝BC ，作MN∥BG交CD于点L ，交FG于点N ．欧几里得在《几何原本》中利用该图解释了（a+b）（a﹣b）＝a²﹣b² ，连接AC ，记△ABC的面积为S₁ ，图中阴影部分的面积为S₂ ．若a＝3b ，则 $\frac{S_{1}}{S_{2}}$ 的值为（）

A、 $\frac{3}{2}$ B、 $\frac{7}{18}$ C、 $\frac{3}{4}$ D、 $\frac{5}{4}$

查看试题解析
5. 商丘宁陵酥梨素以香甜饱满、酥脆多汁享誉省内外，深受大家欢迎．为提高果农筛选酥梨的效率，小明设计了如图甲所示的自动筛选装置．电源电压不变，R₀为定值电阻，R为压敏电阻，阻值随压力大小的变化关系如图乙所示．一次筛选中，小明设计了当经过压力检测区上酥梨质量不大于100g时，机械装置通过传感器操作启动，将质量不达标的小酥梨推出传送带，实现自动筛选功能（g取10N/kg ，例如，物体质量为100g时，压力F＝G＝mg＝0.1kg×10N/kg＝1N）．以下说法错误的是（）

A、酥梨质量越大，压敏电阻R的阻值越小 B、当压力检测区没有酥梨时，压敏电阻的阻值为100Ω C、压敏电阻的阻值R与酥梨质量N成反比例关系 D、当机械装置实现自动筛选功能时，压敏电阻R的范围为60≤R＜100Ω

查看试题解析
6. 有一列数{﹣1，﹣2，﹣3，﹣4}，将这列数中的每个数求其相反数得到{1，2，3，4}，再分别求与1的和的倒数，得到{ $\frac{1}{2}$ ， $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{5}$ }，设为{a₁ ， a₂ ， a₃ ， a₄}，称这为一次操作；第二次操作是将{a₁ ， a₂ ， a₃ ， a₄}再进行上述操作，得到{a₅ ， a₆ ， a₇ ， a₈}；第三次将{a₅ ， a₆ ， a₇ ， a₈}重复上述操作，得到{a₉ ， a₁₀ ， a₁₁ ， a₁₂}……以此类推，得出下列说法中，正确的有（）个．
①a₅＝2， $a_{6} = \frac{3}{2}$ ， $a_{7} = \frac{4}{3}$ ， $a_{8} = \frac{5}{4}$
②a₂₀₁₅＝3
③a₁+a₂+a₃+……+a₄₉+a₅₀＝﹣ $\frac{113}{10}$

A、0 B、1 C、2 D、3

查看试题解析
7. 如图，已知矩形ABCD中，AB＝4cm ， BC＝8cm ，动点P在边BC上从点B向点C运动，速度为1cm/s ．同时动点Q从点C出发，沿折线C→D→A运动，速度为2cm/s ，当一个点到达终点时，另一个点也随之停止运动，设点P运动的时间为t（s），△BPQ的面积为S（cm²），则描述S（cm²）与时间t（s）的函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析
8. 如图，大小两个量角器的零度线都在直线AB上，而且小量角器的中心在大量角器的外边缘上．如果它们外边缘上的公共点P在大量角器上对应的度数为50°，那么∠PBA为的度数（）

A、30° B、32.5° C、35° D、37.5°

查看试题解析

二、多选题（本题共4小题，每小题4分，共16分.在每小题给出的四个选项中，有多项符合题目要求。全部选对得4分，选对但不全得2分，有选错的得0分）

9. 如图是抛物线y＝ax²+bx+c（a＜0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：①3a+b＝0；②b²＝4a（c﹣n）；③一元二次方程ax²+bx+c＝n﹣1无实数根；④ a+b≥am²+bm（m为任意实数）；其中正确结论的是（）

A、① B、② C、③ D、④

查看试题解析
10. 海水受日月引力而产生的周期性运动叫潮汐，早晨海水上涨为潮，黄昏海水上涨为汐，合称潮汐．受潮汐影响，某港口从某日0时到12时的水深h（单位：m）随时间t（单位：h）变化的关系如图1所示，船舶可以根据吃水深度选择进出港口的时间．下列说法中正确的是（）

A、当3＜t＜9时，水深h随着t的增大而减小 B、当t＝9时，该港口水深最浅 C、港口水深h＝6m时，t＝5 D、某货船吃水深度为3m时，则它不可以在上午7时进出港口

查看试题解析
11. 如图，已知四边形ABCD是边长为4的正方形，E是CD上一动点，将△ADE沿直线AE折叠后，点D落在点F处，DF的延长线交BC于点G ， EF的延长线交BC于点H ， AE与DG交于点O ，连接OC ．则下列结论中：①AE＝DG；②EH＝DE+BH；③OC的最小值为2 $\sqrt{5}$ ﹣2；④当点H为BC的中点时，∠CFG＝45°．其中正确的有（）

A、① B、② C、③ D、④

查看试题解析
12. 如图，AB是⊙O的直径，点C是⊙O上一点，AD与过点C的切线垂直，垂足为D ，直线DC与AB的延长线交于点P ，弦CE平分∠ACB ，交AB于点F ，连接BE ， BE＝7 $\sqrt{2}$ ．下列四个结论：①AC平分∠DAB；②PF²＝PB•PA；③若BC＝ $\frac{1}{2}$ OP ，则阴影部分的面积为 $\frac{7}{4}$ π﹣ $\frac{49 \sqrt{3}}{4}$ ；④若PC＝24，则tan∠PCB＝ $\frac{3}{4}$ ．其中正确的是（）

A、① B、② C、③ D、④

查看试题解析

三、填空题（本题共4小题，每小题4分，共16分）

13. 全班约 $\frac{2}{5}$ 是男生，约 $\frac{3}{5}$ 是女生，若根据所给数据绘制扇形统计图，则男生所占的圆心角应为．

查看试题解析
14. 公元三世纪，我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”如图所示，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形，其中直角三角形中较大的锐角度数为α，若大正方形的面积为13，小正方形的面积为1，则sinα﹣cosα的值为．

查看试题解析
15. 若关于x的一元一次不等式组 $\{\begin{matrix} 4 x - 1 > 3 (x + 2) \\ a - 2 x \leq 5 \end{matrix}$ 的解集为x＞7，且关于y的分式方程 $\frac{y + 2 a}{y - 1} + \frac{3 y - 8}{1 - y} = 2$ 的解是非负整数，则所有满足条件的整数a的值之和是．

查看试题解析
16. 把标准纸一次又一次对开，可以得到均相似的“开纸”．现在我们在长为2 $\sqrt{2}$ 、宽为1的矩形纸片中，画两个小矩形，使这两个小矩形的每条边都与原矩形纸的边平行，或小矩形的边在原矩形的边上，且每个小矩形均与原矩形纸相似，然后将它们剪下，则所剪得的两个小矩形纸片周长之和的最大值是．

查看试题解析

四、解答题（本题共6小题，共52分）

17. 如果方程x²+px+q＝0的两个根是x₁、x₂ ，那么x₁+x₂＝﹣p ， x₁•x₂＝q ．
请根据以上结论，解决下列问题：

(1)、已知方程x²+（k﹣2）x﹣2k＝0的两根x₁、x₂之和x₁+x₂＝1，求x₁、x₂；

(2)、如果a、b满足a²+2a﹣2＝0、b²+2b﹣2＝0，求 $\frac{a}{b} + \frac{b}{a}$ 的值．

查看试题解析
18. 为提高新会陈皮知名度，树立品牌意识，我区有关部门对A、B、C、D四个商家销售的礼盒装柑普茶共2000盒进行合格率检测，通过检测得出C厂家的合格率为95%，并根据检测数据绘制了如图1、图2两幅不完整的统计图．

(1)、求抽查D商家的柑普茶盒数，扇形统计图中D商家对应的圆心角的度数；

(2)、抽查C商家的柑普茶是多少盒？其中合格柑普茶是多少盒？并将图1补充完整；

(3)、若要从A、B、C、D四个商家中，随机抽取两个商家代表新会参加广东省特色产品展销会，请用“列表法”或“画树形图”的方法求出C、D两个商家同时被选中的概率．

查看试题解析
19. 如图，在平面直角坐标系xOy中，直线l：y=- $\frac{1}{2}$ x+4与x轴、y轴分别交于点A、B ，与双曲线 $y = \frac{k}{x} (x < 0)$ 相交于点C ，点C在第二象限且△CAO的面积为20．点D（﹣5，m）在双曲线上．

(1)、求点C的坐标以及k的值；

(2)、联结CD ，直线l向上平移交直线CD于点P ，点Q为平面内任意一点，如果四边形ACPQ为菱形，求点P的坐标；

查看试题解析
20. 某超市每天能销售河南特产“伊川富硒小米”和“伊川贡小米”共21袋（5斤装），且“伊川富硒小米”6天销售的袋数与“伊川贡小米”8天销售的袋数相同.

(1)、该超市每天销售“伊川富硒小米”和“伊川贡小米”各多少袋？

(2)、“伊川富硒小米”每袋进价20元，售价25元；“伊川贡小米”每袋进价30元，售价33元.若超市打算购进“伊川富硒小米”和“伊川贡小米”共80袋，其中“伊川富硒小米”不超过40袋，要求这80袋小米全部销售完后的总利润不少于316元，则该超市如何购进这两种小米获利最大？最大利润是多少元？

查看试题解析
21. 如图1，两个全等的直角三角形纸片ABC和DEF拼在一起，使点A与点F重合，点C与点D重合，其中∠ACB＝∠DFE＝90°，BC＝EF＝3cm ， AC＝DF＝4cm ．

(1)、将图1中的三角形纸片DEF沿AC方向平移，连接AE ， BD（如图2），当点F与点C重合时停止平移，试判断四边形ABDE的形状，并说明理由；

(2)、当三角形纸片DEF平移到某一位置时，四边形ABDE恰为矩形（如图3），求AF的长；

(3)、在图3中，取AD的中点O ，再将纸片DEF绕点O顺时针方向旋转α度（0≤α≤90），连接OB ， OE（如图4）．当EF平分∠AEO时，探究OF与BD的数量关系，并说明理由．

查看试题解析
22. 如图1，已知二次函数y＝x²+bx+c的图象与x轴交于点A（﹣1，0）和点B（3，0），与y轴的负半轴交于点C ．

(1)、求这个函数的解析式；

(2)、点P是抛物线上位于第四象限内的一点，当△PBC的面积最大时，点P的坐标，并求出最大面积；

(3)、如图2，点T是抛物线上一点，且点T与点C关于抛物线的对称轴对称，过点T的直线TS与抛物线有唯一的公共点，直线MN∥TS交抛物线于M ， N两点，连AM交y轴正半轴于G ，连AN交y轴负半轴于H ，求OH﹣OG ．

查看试题解析

湖南省岳阳市汨罗市2023-2024学年九年级下学期学习能力检测竞赛数学试题

一、单选题（ 本题共8小题，每小题2分，共16分）

二、多选题（ 本题共4小题，每小题4分，共16分.在每小题给出的四个选项中，有多项符合题目要求。全部选对得4分，选对但不全得2分，有选错的得0分）

三、填空题（ 本题共4小题，每小题4分，共16分）

四、解答题（ 本题共6小题，共52分）

一、单选题（本题共8小题，每小题2分，共16分）

二、多选题（本题共4小题，每小题4分，共16分.在每小题给出的四个选项中，有多项符合题目要求。全部选对得4分，选对但不全得2分，有选错的得0分）

三、填空题（本题共4小题，每小题4分，共16分）

四、解答题（本题共6小题，共52分）