广东省肇庆市怀集县2024年中考二模数学试卷

试卷更新日期：2024-06-17 类型：中考模拟

进入出卷网下载

一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。

1. $2024$ 的倒数是( )

A、 $2024$ B、 $- 2024$ C、 $\frac{1}{2024}$ D、 $- \frac{1}{2024}$

查看试题解析
2. 一滴水的质量约为 $0.0000512 k g$ ，将 $0.0000512$ 用科学记数法表示为( )

A、 $0.512 \times 10^{- 4}$ B、 $5.12 \times 10^{- 5}$ C、 $51.2 \times 10^{- 6}$ D、 $512 \times 10^{- 7}$

查看试题解析
3. 有五张仅有编号不同的卡片，编号分别是 $1$ ， $2$ ， $3$ ， $4$ ， $5 .$ 从中随机抽取一张，编号是奇数的概率为( )

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
4. 我国杨秉烈先生在上世纪八十年代发明了繁花曲线规画图工具，利用该工具可以画出许多漂亮的繁花曲线，繁花曲线的图案在服装、餐具等领域都有广泛运用．下面四种繁花曲线中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 如图所示是一个正方体的展开图，把展开图折叠成小正方体，与“读”字相对面的字是( )

A、悦 B、花 C、都 D、美

查看试题解析
6. 下列运算中，正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{15} \div \sqrt{5} = \sqrt{3}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
7. 如图，四边形 $A B C D$ 是 $⊙ O$ 的内接四边形，若 $∠ B = 120 °$ ，则 $∠ A O C$ 的大小为( )

A、 $130 °$ B、 $50 °$ C、 $100 °$ D、 $120 °$

查看试题解析
8. 为丰富乡村文体生活，某区准备组织首届“美丽乡村”篮球联赛，赛制为单循环形式 $($ 每两队之间都赛一场 $)$ ，计划安排 $28$ 场比赛，设邀请 $x$ 个球队参加比赛，可列方程得( )

A、 $\frac{1}{2} x (x - 1) = 28$ B、 $\frac{1}{2} x (x + 1) = 28$ C、 $x (x - 1) = 28$ D、 $x (x + 1) = 28$

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x (a \neq 0)$ 的图象如图所示，则一次函数 $y = a x + b (a \neq 0)$ 的图象大致为( )

A、 B、 C、 D、

查看试题解析
10. 甲、乙两种物质的溶解度 $y (g)$ 与温度 $t (℃)$ 之间的对应关系如图所示，则下列说法中，错误的是（）

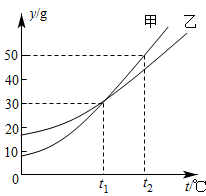A、甲、乙两种物质的溶解度均随着温度的升高而增大 B、当温度升高至 $t_{2} ℃$ 时，甲的溶解度比乙的溶解度大 C、当温度为 $0 ℃$ 时，甲、乙的溶解度都小于 $20 g$ D、当温度为 $30 ℃$ 时，甲、乙的溶解度相等

查看试题解析

二、填空题：本题共5小题，每小题3分，共15分。

11. 要使分式 $\frac{1}{x - 3}$ 有意义，则 $x$ 的取值范围是．

查看试题解析
12. 因式分解： $a x + a y =$ .

查看试题解析
13. 已知一次函数 $y = - x + m$ 与 $y = 2 x - 1$ 的图象如图所示，则关于 $x$ ， $y$ 的方程组 $\{\begin{array}{l} y = - x + m \\ y = 2 x - 1 \end{array}$ 的解为．

查看试题解析
14. 如图， $l_{1} / / l_{2}$ ， $A$ 、 $B$ 分别是直线 $l_{1}$ ， $l_{2}$ 上的点， $A B = 3$ ， $s i n α = \frac{2}{3}$ ，则直线 $l_{1}$ 与 $l_{2}$ 之间的距离为．

查看试题解析
15. 如图， $△ A B C$ 中， $∠ C = 90 °$ ， $∠ B = 30 °$ ， $A C = \sqrt{3}$ ，以 $C$ 为圆心， $C A$ 为半径的圆弧分别交 $A B$ 、 $C B$ 于点 $D$ 、 $E$ ，则图中阴影部分面积之和为．

查看试题解析

三、解答题：本题共8小题，共75分。解答应写出文字说明，证明过程或演算步骤。

16.

(1)、解方程组： $\{\begin{array}{l} 2 x + y = 13 \\ 2 x - y = 3 \end{array}$ ．

(2)、计算： $| - 3 | - 6 s i n 60 ° - (3.14 - π)^{0} + \sqrt{27} + (- \frac{1}{2})^{- 2}$ ．

查看试题解析
17. 以下是某同学化简分式 $(\frac{x + 1}{x^{2} - 4} - \frac{1}{x + 2}) \div \frac{3}{x - 2}$ 的部分运算过程：
解：原式 $= [\frac{x + 1}{(x + 2) (x - 2)} - \frac{1}{x + 2}] \times \frac{x - 2}{3} ①$

$= [\frac{x + 1}{(x + 2) (x - 2)} - \frac{x - 2}{(x + 2) (x - 2)}] \times \frac{x - 2}{3} ②$

$= \frac{x + 1 - x - 2}{(x + 2) (x - 2)} \times \frac{x - 2}{3} ③$
$\dots$
解：

(1)、上面的运算过程中第步出现了错误；

(2)、请你写出完整的解答过程．

查看试题解析
18. 问题情境：
在数学探究活动中，老师给出了如图的图形及下面三个等式：① $A B = A C$ ② $D B = D C$ ③ $∠ B A D = ∠ C A D$ 若以其中两个等式作为已知条件，能否得到余下一个等式成立？

解决方案：探究 $△ A B D$ 与 $△ A C D$ 全等．

问题解决：

(1)、当选择①②作为已知条件时， $△ A B D$ 与 $△ A C D$ 全等吗？（填“全等”或“不全等”），理由是；

(2)、当任意选择两个等式作为已知条件时，请用画树状图法或列表法求 $△ A B D ≌ △ A C D$ 的概率．

查看试题解析
19. 如图，在菱形ABCD中，对角线AC ， BD相交于点O；

(1)、尺规作图：过点C作AB的垂线，垂足为E；（不写作法，保留作图痕迹）

(2)、若AC＝4，BD＝2，求cos∠BCE的值．

查看试题解析
20. 如图，一次函数 $y = k_{1} x + b$ 的图象与反比例函数 $y = \frac{k_{2}}{x}$ 的图象相交于 $A$ 、 $B$ 两点，其中点 $A$ 坐标为 $(1,4)$ ，点 $B$ 坐标为 $(4, n)$ ．

(1)、求这两个函数的解析式；

(2)、将直线 $A B$ 向下平移，若平移后的直线与反比例函数的图象只有一个交点，请说明直线 $A B$ 向下平移了几个单位长度．

查看试题解析
21. “七 $\cdot$ 一”建党节前夕，某校决定购买 $A$ ， $B$ 两种奖品，用于表彰在“童心向党”活动中表现突出的学生．已知 $A$ 奖品比 $B$ 奖品每件多 $25$ 元，预算资金为 $1700$ 元，其中 $800$ 元购买 $A$ 奖品，其余资金购买 $B$ 奖品，且购买 $B$ 奖品的数量是 $A$ 奖品的 $3$ 倍．

(1)、求 $A$ ， $B$ 奖品的单价；

(2)、购买当日，正逢该店搞促销活动，所有商品均按原价八折销售，故学校调整了购买方案：不超过预算资金且购买 $A$ 奖品的资金不少于 $720$ 元， $A$ ， $B$ 两种奖品共 $100$ 件，求购买 $A$ ， $B$ 两种奖品的数量，有哪几种方案？

查看试题解析
22. 如图， $A B$ 是 $⊙ O$ 的直径， $C D$ 是 $⊙ O$ 的一条弦， $C D ⊥ A B$ ，直线 $C E$ 为 $⊙ O$ 的切线， $C E$ 交 $A B$ 的延长线于点 $E$ ，连接 $D B$ 、 $B C$ 、 $C A$ ．

(1)、求证： $∠ B D C = ∠ B C E$ ；

(2)、连接 $D O$ ，延长 $D O$ 交 $A C$ 于点 $F$ ，延长 $D B$ 交 $C E$ 于点 $G .$ 当 $F$ 为 $A C$ 的中点时，求证： $D G ⊥ C E$ ；

(3)、若 $⊙ O$ 的半径为 $6$ ，在 $(2)$ 的条件下，求图中阴影部分面积．

查看试题解析
23. 如图 $1$ ，射线 $O M ⊥ O N$ ，点 $B$ 在 $O N$ 上，且 $O B = 4$ ，点 $A$ 是射线 $O M$ 上的动点．

(1)、当 $O A = O B$ 时，
①求 $∠ A B O$ 的度数；
②如图 $2$ ，若 $P$ 是 $∠ M O N$ 内的一点， $∠ A P B = 90 °$ 且 $P A + P B = 5 \sqrt{2}$ ，求线段 $P O$ 的长；

(2)、如图 $3$ 以 $A B$ 为直角边构造 $R t △ A B C$ ，其中 $∠ B A C = 90 °$ ，且 $S_{△ A B C} = 12$ ，点 $D$ 是线段 $B C$ 的中点，点 $E$ 与点 $A$ 关于点 $D$ 对称，连接 $O E$ ，当线段 $O E$ 取最大值时，求 $\frac{A C}{A B}$ 的值．

查看试题解析