湖南省衡阳市衡阳县2024年中考数学模拟考试试卷

试卷更新日期：2024-06-17 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10个小题，每小题3分，共30分，在每小题给出的四个选项中，只有一项是符合题目要求的；请将你认为正确的选项填涂到答题卡上）

1. 下列四个数中，最小的数是（）

A、 $- 2$ B、 $- 1$ C、0 D、 $π$

查看试题解析
2. 下列运算中正确的是（）

A、 $a^{3} - a^{2} = a$ B、 $a^{3} \cdot a^{4} = a^{12}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 $(- a^{2})^{3} = - a^{6}$

查看试题解析
3. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 太阳直径大约是1392000千米，相当于地球直径的109倍．数据1392000用科学记数法表示为（）

A、 $0.1392 \times 1 0^{7}$ B、 $1.392 \times 1 0^{6}$ C、 $139.2 \times 1 0^{4}$ D、 $1392 \times 1 0^{3}$

查看试题解析
5. 下列长度的三条线段，能组成三角形的是（　　）

A、1，3，4 B、2，2，7 C、4，5，7 D、3，3，6

查看试题解析
6. 下列说法正确的是（）

A、了解一批灯泡的使用寿命，应采用抽样调查的方式 B、为了直观地介绍某款牛奶各营养成分的百分比，最适合使用的统计图是条形统计图 C、一个抽奖活动中，中奖概率为 $\frac{1}{20}$ ，表示抽奖20次必有1次中奖 D、“投掷一枚质地均匀的硬币一次，结果正面朝上”为必然事件

查看试题解析
7. 在平面直角坐标系中，将点 $(2 ， 1)$ 向下平移3个单位长度，所得点的坐标是（）

A、 $(- 1 ， 1)$ B、 $(5 ， 1)$ C、 $(2 ， 4)$ D、 $(2 ， - 2)$

查看试题解析
8. 将含30°角的直角三角板的一个顶点按如图方式放置在直尺上， $∠ 1 = 23 °$ ，则 $∠ 2$ 的度数是（）

A、23° B、53° C、60° D、67°

查看试题解析
9. 我国南宋数学家杨辉在1275年提出的一个问题：“直田积八百六十四步，只云阔不及长一十二步．问阔及长各几步．”意思是：长方形的面积是864平方步，宽比长少12步，问宽和长各是几步．设宽为 $x$ 步，根据题意列方程正确的是（）

A、 $2 x + 2 (x + 12) = 864$ B、 $x^{2} + (x + 12) 2 = 864$ C、 $x (x - 12) = 864$ D、 $x (x + 12) = 864$

查看试题解析
10. 如图， $A B$ 是半 $⊙ O$ 的直径，点C在半 $⊙ O$ 上， $A B = 5 c m$ ， $A C = 4 c m$ .D是 $\overset{⌢}{B C}$ 上的一个动点，连接 $A D$ ，过点C作 $C E ⊥ A D$ 于点E ，连接 $B E$ .在点D移动的过程中， $B E$ 的最小值为（）

A、1 B、 $\sqrt{13} - 2$ C、 $2 \sqrt{2} - 1$ D、3

查看试题解析

二、填空题（本大题共8个小题，每小题3分，共24分；请将答案填在答题卡的答案栏内）

11. 因式分解： $x^{3} - x$ = ．

查看试题解析
12. 分式方程 $\frac{4}{x - 2} = \frac{2}{x}$ 的解是．

查看试题解析
13. 某校评选先进班集体，从“学习”“卫生”“纪律”“活动参与”四个方面综合考核打分，各项满分均为100分，所占比例如下表：
项目
学习
卫生
纪律
活动参与
所占比例
40%
30%
20%
10%
某班这四项得分依次为83，82，73，80，则该班四项综合得分为分.

查看试题解析
14. 如图，点A是反比例函数y＝ $\frac{k}{x}$ 图象上的一个动点，过点A作AB⊥x轴，AC⊥y轴，垂足分别为B，C，矩形ABOC的面积为4，则k＝.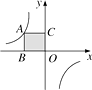

查看试题解析
15. 如果一个多边形每一个外角都是 $60 °$ ，那么这个多边形的边数为．

查看试题解析
16. 如图是一个隧道的横截面，它的形状是以点O为圆心的圆的一部分，如果C是 $⊙ O$ 中弦 $A B$ 的中点， $C D$ 经过圆心O交 $⊙ O$ 于点D ，并且 $A B = 4 m$ ， $C D = 6 m$ ，则 $⊙ O$ 的半径长为m.

查看试题解析
17. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = B C$ .以点A为圆心，以任意长为半径作弧，分别交 $A B$ ， $A C$ 于D ， E点；分别以点D ， E为圆心，以大于 $\frac{1}{2} D E$ 长为半径作弧，在 $∠ B A C$ 内两弧相交于点P；作射线 $A P$ 交 $B C$ 于点F ，过点F作 $F G ⊥ A B$ ，垂足为G.若 $A B = 8 c m$ ，则 $△ B F G$ 的周长等于 $c m$ .

查看试题解析
18. 如图，直线y₁=k₁x与直线y₂=k₂x+b交于点A（1，2）．当y₁<y₂时，x的取值范围是．

查看试题解析

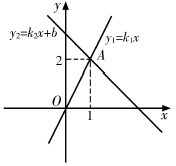
三、解答题（本大题共8个小题，第19-25题每题8分，第26题10分，共66分；解答应写出必要的文字说明、演算步骤或证明过程）

19. 计算： $| - \sqrt{3} | - (4 - π)^{0} - 2 s i n 60 ° + {(\frac{1}{5})}^{- 1}$ ．

查看试题解析
20. 先化简，后求值： ${(x - 2 y)}^{2} + (x - 2 y) (x + 2 y) - x (x - 4 y)$ ，其中 $x = 1, y = - 1$ .

查看试题解析
21. 如图， $A E ⊥ D B$ ， $C F ⊥ D B$ ，垂足分别是点E ， F ， $D E = B F$ ， $A B = C D$ .

(1)、求证： $∠ A = ∠ C$ ；

(2)、若 $A E = 2$ ， $D C = 4$ ，求 $D F$ 的长.

查看试题解析
22. 某学校为扎实推进劳动教育，把学生参与劳动教育情况纳入积分考核.学校抽取了部分学生的劳动积分（积分用x表示）进行调查，整理得到如下不完整的统计表和扇形统计图.
等级
劳动积分
人数
A
$x \geq 90$
4
B
$80 \leq x < 90$
m
C
$70 \leq x < 80$
20
D
$60 \leq x < 70$
8
E
$x < 60$
3
请根据图表信息，解答下列问题：

(1)、统计表中 $m =$ ， C等级对应扇形的圆心角的度数为；

(2)、学校规定劳动积分大于或等于80的学生为“劳动之星”.若该学校共有学生2000人，请估计：该学校“劳动之星”大约有多少人？

(3)、A等级中有两名男同学和两名女同学，学校从A等级中随机选取2人进行经验分享，请用列表法或画树状图法，求恰好抽取一名男同学和一名女同学的概率.

查看试题解析
23. 如图，已知等腰 $△ A B C$ ， $A B = A C$ ，以 $A B$ 为直径作 $⊙ O$ 交 $B C$ 于点D ，过D作 $D F ⊥ A C$ 于点E ，交 $B A$ 的延长线于点F；

(1)、求证： $D F$ 是 $⊙ O$ 的切线；

(2)、若 $C E = \sqrt{3}$ ， $C D = 2$ ，求图中阴影部分的面积（结果用 $π$ 表示）.

查看试题解析
24. 某商城在端午节期间促销海尔冰箱，每台进货价为2500元，标价为3000元.

(1)、商城举行了“新老用户粽是情”摸奖活动，中奖者商城将冰箱连续两次降价，每次降价的百分率相同，最后以2430元售出，求每次降价的百分率；

(2)、市场调研表明：当每台售价为2900元时，平均每天能售出8台；当每台售价每降50元时，平均每天就能多售出4台.若商城要想使海尔冰箱的销售利润平均每天达到5000元，则每台冰箱的定价应为多少元？

查看试题解析
25. 某校数学社团开展“探索生活中的数学”研学活动，小亮想测量某大厦楼顶上的一个广告牌 $C D$ 的高度，从与大厦 $B C$ 相距 $30 m$ 的A处观测广告牌顶部D的仰角 $∠ B A D = 30 °$ ，观测广告牌底部C的仰角为 $∠ B A C = 27 °$ ，如图所示.

(1)、求大厦 $B C$ 的高度；（结果精确到 $0.1 m$ ）

(2)、求广告牌 $C D$ 的高度.（结果取整数）
（参考数据： $s i n 27 ° \approx 0.454$ ， $c o s 27 ° \approx 0.891$ ， $t a n 27 ° \approx 0.510$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
26. 如图1，在平面直角坐标系 $x O y$ 中，已知抛物线 $y = a x^{2} + b x - 6 (a \neq 0)$ 与x轴交于点 $A (- 2, 0)$ ， $B (6, 0)$ ，与y轴交于点C ，顶点为D ，连接 $B C$ .

(1)、求抛物线的解析式；

(2)、在图1中，连接 $A C$ 并延长交 $B D$ 的延长线于点E ，求 $∠ C E B$ 的度数；

(3)、如图2，若动直线l与抛物线交于M ， N两点（直线l与 $B C$ 不重合），连接 $C N$ ， $B M$ ，直线 $C N$ 与 $B M$ 交于点P.当 $M N ∥ B C$ 时，点P的横坐标是否为定值？请说明理由.

查看试题解析

项目	学习	卫生	纪律	活动参与
所占比例	40%	30%	20%	10%

等级	劳动积分	人数
A	$x \geq 90$	4
B	$80 \leq x < 90$	m
C	$70 \leq x < 80$	20
D	$60 \leq x < 70$	8
E	$x < 60$	3