云南省昭通市绥江县2023-2024学年七年级下册4月月考数学试题

试卷更新日期：2024-06-17 类型：月考试卷

进入出卷网下载

一、选择题（本大题共15小题，每小题只有一个正确选项，每小题2分，共30分）

1. 第19届亚运会于2023年9月23日至10月8日在杭州举行，杭州奥体中心体育场占地面积430亩，共有80800个座位，其中数80800用科学记数法表示为（）

A、 $80.8 \times 1 0^{3}$ B、 $8.08 \times 1 0^{3}$ C、 $8.08 \times 1 0^{4}$ D、 $0.808 \times 1 0^{5}$

查看试题解析
2. 如图，直线a、b被直线c所截， $∠ 2$ 与 $∠ 5$ 是（）

A、同位角 B、内错角 C、同旁内角 D、对顶角

查看试题解析
3. 下列计算正确的是（）

A、 $\pm \sqrt{4} = 2$ B、 $\sqrt{16} = 4$ C、 $\sqrt{(- 3)^{2}} = - 3$ D、 $- \sqrt{(- 2)^{2}} = 2$

查看试题解析
4. 如图，下列条件中不能判定AB∥CD的是（）

A、∠1＋∠4＝180° B、∠2＝∠6 C、∠5＋∠6＝180° D、∠3＝∠5

查看试题解析
5. 如图，斑马线的作用是为了引导行人安全地通过马路．小丽觉得行人沿垂直马路的方向走过斑马线更为合理，这一想法体现的数学依据是（）

A、过一点有且只有一条直线与已知直线垂直 B、垂线段最短 C、两点之间，线段最短 D、两点确定一条直线

查看试题解析
6. 下列命题是真命题的是（）

A、相等的角是对顶角 B、若数a、b满足 $a^{2} = b^{2}$ ，则 $a = b$ C、垂直于同一条直线的两条直线互相平行 D、垂线段最短

查看试题解析
7. 估计 $\sqrt{35}$ 的值（）

A、在 $6$ 和 $7$ 之间 B、在 $5$ 和 $6$ 之间 C、在 $3$ 和 $4$ 之间 D、在 $2$ 和 $3$ 之间

查看试题解析
8. 下列说法正确的是（）

A、25的平方根是 $\pm 5$ B、 $\sqrt{16}$ 的平方根是 $\pm 4$ C、 $- 36$ 的算术平方根是6 D、4的平方根是2

查看试题解析
9. 如图为2023年杭州亚运会吉祥物宸宸，下列图案中，是通过该图平移得到的图案是（）

A、 B、 C、 D、

查看试题解析

10. 下面是嘉琪同学做的练习题，她做对了（）道．

填空题：

（1） $\sqrt{4}$ 的相反数是 $- 2$

（2）算术平方根等于它本身的数有0和1

（3） $| 3 - π | = 3 - π$

（4） $- \sqrt{\frac{4}{9}}$ 的倒数是 $\frac{3}{2}$

（5）近似数5.2万精确到了千位

（6）已知 $\sqrt{a + 3} + | b - 1 | = 0$ ，则 $a + b = 2$

A、5 B、4 C、3 D、2

查看试题解析

11. 若 $2 m - 4$ 与 $3 m - 1$ 是同一个正数的平方根，则m为（）

A、 $- 3$ B、1 C、 $- 1$ D、 $- 3$ 或1

查看试题解析
12. 如图，若 $A B ∥ C D$ ，则 $∠ α$ 、 $∠ β$ 、 $∠ γ$ 之间关系是（）

A、 $∠ α + ∠ β + ∠ γ = 180 °$ B、 $∠ α + ∠ β - ∠ γ = 360 °$ C、 $∠ α + ∠ β - ∠ γ = 180 °$ D、 $∠ α - ∠ β + ∠ γ = 360 °$

查看试题解析
13. 下列度分秒运算中，正确的是（）

A、48°39^'+67°31^'＝115°10^' B、90°﹣70°39^'＝20°21^' C、21°17^'×5＝185°5^' D、180°÷7＝25°43^'（精确到分）

查看试题解析
14. 长方形窗户上的装饰物如图所示，它是由半径均为b的两个四分之一圆组成，则能射进阳光部分的面积是（）

A、2a²﹣ $\frac{1}{2}$ π²b² B、2a²﹣πb² C、2ab﹣ $\frac{1}{2}$ πb² D、2ab﹣ $\frac{1}{2}$ π²b²

查看试题解析
15. 我国古代数学名著《算法统宗》中，有一道“群羊逐草”的问题，大意是：牧童甲在草原上放羊，乙牵着一只羊来，并问甲：“你的羊群有100只吗？”甲答：“如果在这群羊里加上同样的一群羊，再加上一群的一半，一群的四分之一，再加上你的一只，就是100只.”问牧童甲赶着多少只羊？若设这群羊有 $x$ 只，则下列方程中正确的是（）

A、 $(1 + \frac{1}{2} + \frac{1}{4}) x - 1 = 100$ B、 $x + x + \frac{1}{2} x + \frac{1}{4} x + 1 = 100$ C、 $(1 + \frac{1}{2} + \frac{1}{4}) x + 1 = 100$ D、 $x + x + \frac{1}{2} x + \frac{1}{4} x - 1 = 100$

查看试题解析

二、填空题（本大题共4小题，每小题2分，共8分）

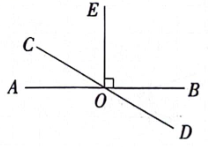
16. 如果a ， b是2024的两个平方根，那么 $a + b + a b =$ ．

查看试题解析
17. 将命题“对顶角相等”改写成“如果…，那么…．”的形式为如果，那么．

查看试题解析
18. 如图，直线AB与CD相交于点O ， $O E ⊥ A B$ ， $∠ C O E = 60 °$ ，则 $∠ B O D$ 等于．

查看试题解析
19. 将连续的偶数2，4，6，8，10，…排成如图所示的数表，若将十字形框上下左右移动，可框出其中的五个数．当框住的五个数字之和为2030时，则位于十字形框中心的数为．

查看试题解析

三、解答题（本大题共8小题，共62分）

20. 计算： $\sqrt{16} + (- 3) - | \sqrt{3} - 2 | + \sqrt{(- 3)^{2}} - (- 1)^{2024}$ ．

查看试题解析
21. 解方程：

(1)、 $x - \frac{3 x - 1}{4} = \frac{x}{6}$

(2)、 $(x + 2)^{2} = 9$

查看试题解析
22. 如图，在 $8 \times 10$ 的正方形网格中，每个小正方形的边长都为1， $△ A B C$ 的顶点均在小正方形的顶点上．

(1)、把 $△ A B C$ 先向右移动5个单位长度，再向下移动3个单位长度得到 $△ A_{1} B_{1} C_{1}$ ，画出 $△ A_{1} B_{1} C_{1}$ （其中点A的对应点为 $A_{1}$ ，点B的对应点为 $B_{1}$ ，点C的对应点为 $C_{1}$ ）；

(2)、连接 $A A_{1}$ ， $B B_{1}$ ，判定 $A A_{1}$ 与 $B B_{1}$ 的位置关系，并写出 $△ A_{1} B_{1} C_{1}$ 的面积．

查看试题解析
23. 如图所示，已知 $∠ 1 = ∠ 2$ ， $A C$ 平分 $∠ D A B$ ，试说明 $D C ∥ A B$ ．

查看试题解析
24. 请将下列证明过程补充完整：
已知：如图， $A E$ 平分 $∠ B A C$ ， $C E$ 平分 $∠ A C D$ ，且 $∠ α + ∠ β = 90 °$ ．求证： $A B ∥ C D$ ．
证明： $∵ C E$ 平分 $∠ A C D$ ，
$∴ ∠ A C D = 2 ∠ α$ （    ）
$∵ A E$ 平分 $∠ B A C$ （已知），
$∴ ∠ B A C =$     ▲    （    ）．
$∴ ∠ A C D + ∠ B A C = 2 ∠ α + 2 ∠ β$ （    ）．
即 $∠ A C D + ∠ B A C = 2 (∠ α + ∠ β)$ ．
$∵ ∠ α + ∠ β = 90 °$ （已知），
$∴ ∠ A C D + ∠ B A C =$     ▲    （    ）．
$∴$     ▲    （    ）．

查看试题解析
25. 请观察下列式子：
$\sqrt{1} = 1$ ； $\sqrt{1 + 3} = \sqrt{4} = 2$ ； $\sqrt{1 + 3 + 5} = \sqrt{9} = 3$ ；
$\sqrt{1 + 3 + 5 + 7} = \sqrt{16} = 4$ ．
根据阅读解决下列问题：

(1)、计算： $\sqrt{1 + 3 + 5 + 7 + 9} =$ ； $\sqrt{1 + 3 + 5 + 7 + 9 + 11} =$ ；

(2)、猜想规律： $\sqrt{1 + 3 + 5 + 7 + 9 + 11 + ⋯ + (2 n - 1)} =$ （n为正整数）；

(3)、若定义 $\sqrt{a \times b} = \sqrt{a} \times \sqrt{b}$ （a ， b都是正整数），
利用上述定义及规律计算 $\sqrt{4 + 12 + 20 + 28 + 36 + 44 + ⋯ + 404}$ 的值．

查看试题解析
26. 三八妇女节到来之际，我校准备购进一批贺卡送给女教师们，贺卡原价8元/张，甲、乙两家商店优惠方式如下：
甲商店：所有贺卡按原价的九折出售；
乙商店：一次性购买不超过20张不优惠，超过部分打八折．
设我校准备购买 $a (a > 20)$ 张贺卡，

(1)、用含 $a$ 的式子分别表示到甲、乙两家商店购买贺卡的费用；

(2)、当我校购买多少张贺卡时，两家商店的费用相同？

(3)、已知贺卡是一张面积为 $144 c m^{2}$ 的正方形，另有一个长宽比为 $5 : 3$ 的长方形信封，面积为 $165 c m^{2}$ ，请问能将这张贺卡不折叠的放入此信封吗？（放入时贺卡与信封的边平行）请通过计算说明你的判断．

查看试题解析
27. 如图，已知直线l₁∥l₂ ，且l₃和l₁、l₂分别交于A、B两点，点P在直线AB上.

(1)、试说明∠1，∠2，∠3之间的关系式；（要求写出推理过程）

(2)、如果点P在A、B两点之间（点P和A、B不重合）运动时，试探究∠1，∠2，∠3之间的关系是否发生变化？（只回答）

(3)、如果点P在A、B两点外侧（点P和A、B不重合）运动时，试探究∠1，∠2，∠3之间的关系.（要求写出推理过程）

查看试题解析