初中数学同步训练必刷培优卷(北师大版七年级下册 第五单元测试卷)
试卷更新日期:2024-06-15 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是( )A、
 B、
B、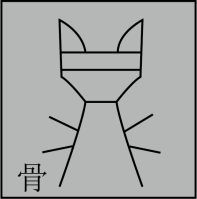 C、
C、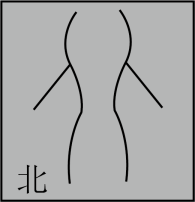 D、
D、 2. 如图,在中,的面积为 , 分别以点为圆心,以大于的长为半径作弧,两弧分别交于 , 连接为的中点,为直线上任意一点.则长度的最小值为( )
2. 如图,在中,的面积为 , 分别以点为圆心,以大于的长为半径作弧,两弧分别交于 , 连接为的中点,为直线上任意一点.则长度的最小值为( )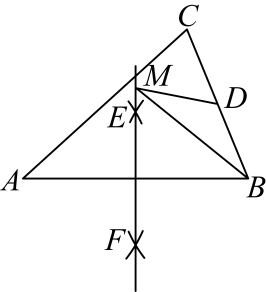 A、 B、 C、 D、3. 如图,将四边形纸片ABCD沿EF折叠,点A落在A1处,若∠1+∠2=90°,则∠A的度数是( )
A、 B、 C、 D、3. 如图,将四边形纸片ABCD沿EF折叠,点A落在A1处,若∠1+∠2=90°,则∠A的度数是( ) A、45° B、40° C、35° D、30°4. 小强将一张正方形纸片按如图所示对折两次,并在如图位置上剪去一个小正方形,然后把纸片展开,得到的图形应是( )
A、45° B、40° C、35° D、30°4. 小强将一张正方形纸片按如图所示对折两次,并在如图位置上剪去一个小正方形,然后把纸片展开,得到的图形应是( ) A、
A、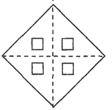 B、
B、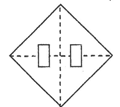 C、
C、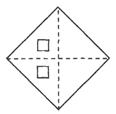 D、
D、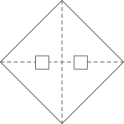 5. 如图,把一张长方形纸片 沿 折叠, ,则 ( )
5. 如图,把一张长方形纸片 沿 折叠, ,则 ( )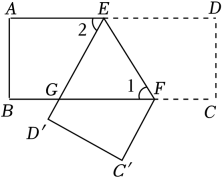 A、 B、 C、 D、6. 如图,四边形是直角梯形, , , 点是腰上的一个动点,要使最小,则点应该满足( )
A、 B、 C、 D、6. 如图,四边形是直角梯形, , , 点是腰上的一个动点,要使最小,则点应该满足( ) A、 B、 C、 D、7. 如图1所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
A、 B、 C、 D、7. 如图1所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着将对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( ) A、
A、 B、
B、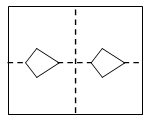 C、
C、 D、
D、 8. 如图, 为等腰直角三角形, 、将 按如图方式进行折叠,使点A与 边上的点F重合,折痕分别与 、 交于点D、点E.下列结论:① ;② ;③ ;④ .其中一定正确的结论有( )
8. 如图, 为等腰直角三角形, 、将 按如图方式进行折叠,使点A与 边上的点F重合,折痕分别与 、 交于点D、点E.下列结论:① ;② ;③ ;④ .其中一定正确的结论有( ) A、1个 B、2个 C、3个 D、4个9.
A、1个 B、2个 C、3个 D、4个9.如图,是把一张长方形的纸片沿长边中点的连线对折两次后得到的图形,再沿虚线裁剪,展开后的图形是( )
 A、
A、 B、
B、 C、
C、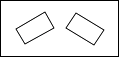 D、
D、 10. 如图,直线l是一条河,P,Q两地相距8千米,P,Q两地到l的距离分别为2千米,5千米,欲在l上的某点M处修建一个水泵站,向P,Q两地供水.现有如下四种铺设方案,则铺设的管道最短的是( )
10. 如图,直线l是一条河,P,Q两地相距8千米,P,Q两地到l的距离分别为2千米,5千米,欲在l上的某点M处修建一个水泵站,向P,Q两地供水.现有如下四种铺设方案,则铺设的管道最短的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题(每题3分,共15分)
-
11. 如图,将长方形纸片 ABCD沿EF 折叠后,点A,B分别落在点 A',B'的位置,再沿 AD 边将∠A'折叠到∠H 处.已知∠1=52°,则∠AEF=°,∠FEH=°
 12. 如图,中, , , , , 将沿折叠,使得点C恰好落在边上的点E处,P为折痕上一动点,则周长的最小值是 .
12. 如图,中, , , , , 将沿折叠,使得点C恰好落在边上的点E处,P为折痕上一动点,则周长的最小值是 . 13. 如图所示,中,且分别为边边上的高,相交于点F, 连接则下列结论中:①垂直平分;②图中有3个等腰三角形;③;④的长度恰与的周长相等;⑤如图,若点P是高上一个动点,点Q是边上一个动点,连接 , 则的最小值等于的长度,其中正确的是(只填序号).
13. 如图所示,中,且分别为边边上的高,相交于点F, 连接则下列结论中:①垂直平分;②图中有3个等腰三角形;③;④的长度恰与的周长相等;⑤如图,若点P是高上一个动点,点Q是边上一个动点,连接 , 则的最小值等于的长度,其中正确的是(只填序号). 14. 如图,锐角内有一定点A,连接 , 点B、C分别为、边上的动点,连接、、 , 设(),当取得最小值时,则 . (用含的代数式表示)
14. 如图,锐角内有一定点A,连接 , 点B、C分别为、边上的动点,连接、、 , 设(),当取得最小值时,则 . (用含的代数式表示)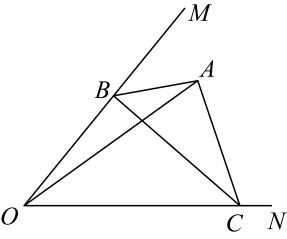 15. 数学活动课上,小明同学尝试将正方形纸片剪去一个小正方形,剩余部分沿虚线剪开,拼成新的图形。现给出下列3种不同的剪、拼方案,其中能够验证平方差公式的方案是 。(请填上正确的序号)
15. 数学活动课上,小明同学尝试将正方形纸片剪去一个小正方形,剩余部分沿虚线剪开,拼成新的图形。现给出下列3种不同的剪、拼方案,其中能够验证平方差公式的方案是 。(请填上正确的序号)
三、作图题(共6分)
-
16. 如图,ABC的顶点A、B、C都在小正方形的顶点上,利用网格线按下列要求画图.

⑴画A1B1C1 , 使它与ABC关于直线l成轴对称;
⑵求ABC的面积;
⑶在直线l上找一点P,使点P到点A、B的距离之和最短(不需计算,在图上直接标记出点P的位置).
四、解答题(共3题,共24分)
-
17. 如图1,将一张长方形纸片沿 EF 折叠,使AB落在A'B'的位置.
 (1)、若∠1 的度数为α,求∠2 的度数(用含α的代数式表示).(2)、如图2,再将纸片沿GH 折叠,使得CD落在C'D'的位置.
(1)、若∠1 的度数为α,求∠2 的度数(用含α的代数式表示).(2)、如图2,再将纸片沿GH 折叠,使得CD落在C'D'的位置.①若EF∥C'G,∠1 的度数为α,求∠3 的度数(用含α的代数式表示).
②若B'F⊥C'G,∠3的度数比∠1 的度数大20°,求∠1的度数.
18. 问题解决: (1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.19. 如图,在中, , 点D为BC边上一点,E为AC延长线上的一点, , F为CB边上一点,连接EF,延长AD交EF于点K, , 过点D作直线于G,延长GD交EF于点H,作平分交AD于点M,过点M作交EF于点N,交GD于点O,交BC于点Q, , 连接GN.
(1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.19. 如图,在中, , 点D为BC边上一点,E为AC延长线上的一点, , F为CB边上一点,连接EF,延长AD交EF于点K, , 过点D作直线于G,延长GD交EF于点H,作平分交AD于点M,过点M作交EF于点N,交GD于点O,交BC于点Q, , 连接GN.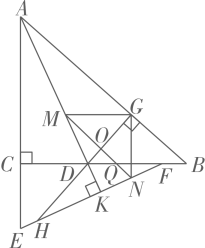 (1)、与相等吗?为什么?(2)、试说明 .
(1)、与相等吗?为什么?(2)、试说明 .五、实践探究题(共3题,共25分)
-
20. 综合与实践:折纸中的数学
【问题提出】在前面的学习中我们通过折纸可以找出一个角的平分线,还可以折出过一个点且与已知直线垂直的直线.那我们能否通过折纸的方式找到过直线外一点且与已知直线平行的直线呢?
 (1)、【知识初探】王玲同学在探究“过直线外一点作已知直线的平行线”的活动中,通过如下的折纸方式找到了符合要求的直线.
(1)、【知识初探】王玲同学在探究“过直线外一点作已知直线的平行线”的活动中,通过如下的折纸方式找到了符合要求的直线.①如图1,在纸上画出一条直线 , 在外取一点 . 过点折叠纸片,使得点的对应点落在直线上(如图2),记折痕与的交点为 , 将纸片展开铺平.则 ▲ ;
②再过点将纸片进行折叠,使得点的对应点落在直线上(如图3),再将纸片展开铺平(如图4).此时王玲说,就是的平行线.王玲的说法正确吗?请写出过程予以证明;
(2)、【拓展延伸】李强同学在王玲同学折纸的基础上,补充了条件:如图5,在线段上任取一点 , 连接 , 请你猜想与这三个角之间的数量关系,并说明理由.21. 【问题呈现】小明在学习中遇到这样一个问题:如图①,在中, , 平分、于D , 猜想、、的数量关系. (1)、小明阅读题目后,没有发现数量关系与解题思路,于是尝试代入、的特殊值求值并寻找它们的数量关系,得到下面几组对应值:(单位:度)
(1)、小明阅读题目后,没有发现数量关系与解题思路,于是尝试代入、的特殊值求值并寻找它们的数量关系,得到下面几组对应值:(单位:度)10
30
30
20
20
70
70
60
60
80
30
a
15
20
30
上表中a= , 猜想与、的数量关系并证明 .
(2)、【变式应用】小明继续研究,在图②中, , , 其它条件不变,若把“于D”改为“点F是线段上任意一点,于D”,则(直接写出结果).
(3)、小明提出问题,在中, , 平分 , 若点F是线段延长线上一点,于D , 试探究与、的数量关系(直接写出结论,不需证明).22. 教材呈现:如图是北师大版七年级下册数学教材第123页的部分内容, (1)、请根据所给教材内容,写出结论:(填“”、“”或“”)(2)、结合教材上的图5—11,证明你的结论.(推理过程请注明理由)(3)、应用上述结论解决下列题目:
(1)、请根据所给教材内容,写出结论:(填“”、“”或“”)(2)、结合教材上的图5—11,证明你的结论.(推理过程请注明理由)(3)、应用上述结论解决下列题目:已知:如图,中,是的垂直平分线,于点D,且D为的中点.

①求证:;(推理过程请注明理由)
②若 , 求的度数.
-