广东省惠州市惠东县2024年中考数学二模试题
试卷更新日期:2024-06-13 类型:中考模拟
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1. 下列各数中,是无理数的是( )A、 B、 C、-1 D、02. 鲁班锁,民间也称作孔明锁、八卦锁,它起源于中国古代建筑中首创的榫卯结构.如图是鲁班锁的其中一个部件,从正面看到的平面图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. “五一”假期全社会跨区域人员流动量约为13.6亿人次,比2019年同期增长24.1%.将数据“13.6亿”用科学记数法表示为( )A、 B、 C、 D、4. 不等式的解集在数轴上表示正确的是( )A、
3. “五一”假期全社会跨区域人员流动量约为13.6亿人次,比2019年同期增长24.1%.将数据“13.6亿”用科学记数法表示为( )A、 B、 C、 D、4. 不等式的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,在菱形ABCD中,对角线AC与BD相交于点O , 交BC于点E . 若 , 则OE的长为( )
5. 下列计算正确的是( )A、 B、 C、 D、6. 如图,在菱形ABCD中,对角线AC与BD相交于点O , 交BC于点E . 若 , 则OE的长为( ) A、6cm B、4cm C、3cm D、2cm7. 下列函数中,y随x增大而减小的是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,已知 , 点B , C的坐标分别是 , , 则点A的坐标是( )
A、6cm B、4cm C、3cm D、2cm7. 下列函数中,y随x增大而减小的是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,已知 , 点B , C的坐标分别是 , , 则点A的坐标是( ) A、 B、 C、 D、9. 如图,在中, , AE平分 , 若 , , 则的度数是( )
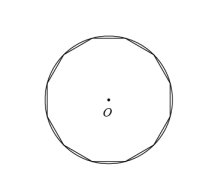
A、 B、 C、 D、9. 如图,在中, , AE平分 , 若 , , 则的度数是( ) A、10° B、12° C、13° D、15°10. 刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( )
A、10° B、12° C、13° D、15°10. 刘徽在《九章算术注》中首创“割圆术”,利用圆的内接正多边形来确定圆周率,开创了中国数学发展史上圆周率研究的新纪元.某同学在学习“割圆术”的过程中,作了一个如图所示的圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( )
 A、1 B、3 C、 D、
A、1 B、3 C、 D、二、填空题:本大题共5小题,每小题3分,共15分.
-
11. 因式分解: .12. 若分式的值为0,则x的值为 .13. 将抛物线先向右平移3个单位长度,再向下平移4个单位长度后,所得到的新抛物线的表达式为 .14. 如图,AB是的直径,点C为外一点,CA , CD分别与相切于点A , D , 连接BD , AD . 若 , 则 .
 15. 如图,在菱形ABCD中,对角线AC与BD相交于点O , 过点D作于点F , 交AC于点E . 已知 , , 则CD的长为 .
15. 如图,在菱形ABCD中,对角线AC与BD相交于点O , 过点D作于点F , 交AC于点E . 已知 , , 则CD的长为 .
三、解答题(一):本大题共3小题,第16题10分,第17、18题各7分,共24分.
-
16.(1)、计算:;(2)、解方程组: .17. 某文具店在一次促销活动中规定:消费者消费满200元就可享受打折优惠.期中考试后,小韦同学在该店为班级买奖品,准备买6支钢笔和若干本笔记本.已知每支钢笔15元,每本笔记本8元,那么她至少买多少本笔记本才能享受打折优惠?18. 小明、小华一起到广州游玩,他们决定在三个热门景点(A.广州塔;B.白云山;C.广州博物馆)中各自随机选择一个景点游玩.(1)、小华选择到广州博物馆游玩的概率是;(2)、用画树状图或列表的方法,求小明、小华选择到不同景点游玩的概率.
四、解答题(二):本大题共3小题,每小题9分,共27分.
-
19. 综合与实践

【实践背景】目前我国已是隧道数量最多、建设规模最大、发展速度最快的隧道大国,我国西部因山地众多,交通不便,因此修建隧道既可缩减通行距离,也可增强两地经济联系.
【问题情境】A县与B县隔山相望,A县要先绕行C地才可到达B县.为缩减路程,A县政府计划修建隧道AB连通A , B两县.
【数据收集】某实践小组利用课余时间到该隧道实地进行数据测量、收集,并绘制如图所示的示意图.经过测量得到 , , .
【问题解决】
(1)、尺规作图:作AB边上的高CD;(保留作图痕迹,不写作法)(2)、修建隧道后的路程比原来缩短了多少千米?(参考数据: , , , , 结果精确到0.01)20. 花坛水池中央有一喷泉,水管 , 水从喷头C喷出后呈抛物线状,先向上至最高点后落下,为增强欣赏效果,喷头C不定时自动升降,上下升降的范围是 . 建立如图所示的平面直角坐标系,水的落地点B距水池中央的水平距离为 , 水流所形成的抛物线L:的最高点距离水面4m. (1)、求a , n的值以及抛物线的顶点坐标;(2)、升降喷头C时,水流所形成的抛物线形状不变.某一时刻,身高1.65m的小丽同学,恰好站在距花坛中心水管2m的位置,则喷头C在升降过程中,水流是否会打湿小丽的头发?21. 如图,正比例函数的图象与反比例函数的图象相交于A , B两点,已知A点的横坐标是2.
(1)、求a , n的值以及抛物线的顶点坐标;(2)、升降喷头C时,水流所形成的抛物线形状不变.某一时刻,身高1.65m的小丽同学,恰好站在距花坛中心水管2m的位置,则喷头C在升降过程中,水流是否会打湿小丽的头发?21. 如图,正比例函数的图象与反比例函数的图象相交于A , B两点,已知A点的横坐标是2. (1)、分别求出这两个函数的表达式;(2)、将直线向下平移m个单位长度,与反比例函数在第一象限的图象交于点C , 与x轴和y轴分别交于点D , E . 若 , 求m的值.
(1)、分别求出这两个函数的表达式;(2)、将直线向下平移m个单位长度,与反比例函数在第一象限的图象交于点C , 与x轴和y轴分别交于点D , E . 若 , 求m的值.五、解答题(三):本大题共2小题,每小题12分,共24分.
-
22. 如图1,已知在中, , , , 点O为BC的中点,分别与AB , AC相切于点D , E , 点P是上的动点,过点P作的切线交AB , AC于点M , N .
 (1)、求点B到线段AC的距离;(2)、如图2,当点P是的中点时,求MN的长;(3)、BM与CN的乘积是否为定值?若是,请求出定值;若不是,请说明理由.23. 综合探究
(1)、求点B到线段AC的距离;(2)、如图2,当点P是的中点时,求MN的长;(3)、BM与CN的乘积是否为定值?若是,请求出定值;若不是,请说明理由.23. 综合探究
【问题情境】综合与实践课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图1是一张矩形纸片ABCD , 其中 , .
【操作发现】
(1)、奋进小组先将图1中的矩形纸片ABCD沿直线BD折叠,使得点C落在点E处,BE交AD于点P , 得到图2,他们发现 . 请你证明这个结论;(2)、创新小组将图1中的矩形纸片折叠,使得点A落在对角线BD上,记为点G , 折痕为BF , 得到图3,则;(3)、【实践探究】希望小组在创新小组操作的基础上,将图3中的纸片展开,然后提出一个问题:将矩形纸片ABCD沿直线AH折叠,使得点B落在对角线BD上的点处,然后将纸片展平,如图4所示,折痕AH交BF于点M , 交BD于点N , 试判断的形状;
(4)、请你根据希望小组的操作,求点G到AD的距离.