江西省上饶市玉山县2024年中考数学二模试题
试卷更新日期:2024-06-13 类型:中考模拟
一、选择题(本大题共6小题,每小题3分,共18分)
-
1. 2024的倒数是( )A、2024 B、 C、 D、2. 下列计算正确的是A、 B、(a3)2=a5 C、 D、3. 下列四个数,属于无理数的是( )A、 B、 C、 D、4. 某工艺品创业小微公司共有12名员工,为了了解每个员工的日均生产能力,随机调查了某天每个员工的生产件数,获得数据如下表:则这一天12名员工生产件数的众数和中位数分别是( )
生产件数(件)
10
11
12
13
14
15
人数(人)
1
4
3
2
1
1
A、4件,11件 B、12件,11件 C、11件,12件 D、4件,3件5. 如图所示是 个大小相同的正方形相连,共有正方形的顶点 个,从中任取 个点为顶点构成正方形,共可以组成正方形的个数为( ) A、 B、 C、 D、6. 反比例函数 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )
A、 B、 C、 D、6. 反比例函数 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )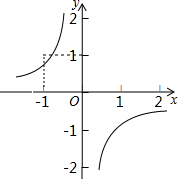 A、
A、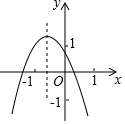 B、
B、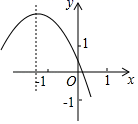 C、
C、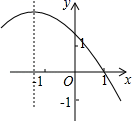 D、
D、
二、填空题(本大题共6小题,每小题3分,共18分)
-
7. 分解因式: .8. 若方程的两根分别是和 , 且 .9. 《九章算术》中有一道题是:“ 今有大器五小器一容三斛,大器小器五容二斛.问大、小器各盛几斛?”大致意思是:有大小两种盛米的桶,大桶加小桶共盛斛米,大桶加小桶共盛斛米,问每个大桶和小桶各盛米多少斛?设每个大桶盛x斛,每个小桶盛斛,则可列方程组为 . (注: 斛是古代一种容量单位)10. 若不等式组 , 仅有一个整数解,则m的取值范围是.11. 如图,将绕点A逆时针旋转得到 , 点D在边上,与交于点F , 若 , 则 .
 12. 如图,在平面直角坐标系中,是的一条直径,已知点和点 , 点是上的一个动点,当线段截所得的三角形与相似时,点的坐标为 .
12. 如图,在平面直角坐标系中,是的一条直径,已知点和点 , 点是上的一个动点,当线段截所得的三角形与相似时,点的坐标为 .
三、解答题(本大题共5小题,每小题6分,共30分)
-
13.(1)、解不等式:;(2)、化简: .14. 如图,四边形 中,点E,F别在AD,BC上,G在AB延长线上,若 , , .求证: .
 15. 如图,以等腰三角形的底边为直径的圆与 , 分别交于点D , E . 请仅用无刻度直尺按下列要求作图(保留作图痕迹).
15. 如图,以等腰三角形的底边为直径的圆与 , 分别交于点D , E . 请仅用无刻度直尺按下列要求作图(保留作图痕迹). (1)、在图1中,作一条与平行的直线;(2)、在图2中,作一个以为对角线的矩形.16. 小辉家大门进门处有一个三位单极开关,如图,每个开关分别控制着A(楼梯),B(客厅),C(走廊)三盏电灯,其中走廊的灯已坏(对应的开关闭合也不会亮).
(1)、在图1中,作一条与平行的直线;(2)、在图2中,作一个以为对角线的矩形.16. 小辉家大门进门处有一个三位单极开关,如图,每个开关分别控制着A(楼梯),B(客厅),C(走廊)三盏电灯,其中走廊的灯已坏(对应的开关闭合也不会亮). (1)、若小惠任意闭合一个开关,“楼梯灯亮了”是事件;
(1)、若小惠任意闭合一个开关,“楼梯灯亮了”是事件;若小惠闭合所有三个开关,“楼梯,客厅,走廊灯全亮了”是事件.(填“不可能”“必然”或“随机”)
(2)、若任意闭合其中两个开关,试用画树状图或列表的方法求“客厅和楼梯灯都亮了”的概率.17. 如图,已知矩形的两边OA,OC分别落在轴,轴的正半轴上,的坐标为 , 反比例函数的图象经过的中点E,且与BC边相交于点D. (1)、①求反比例函数的解析式及点D的坐标;
(1)、①求反比例函数的解析式及点D的坐标;②直接写出的面积为 ▲ .
(2)、若P是OA上的动点,当值为最小时,求直线的解析式.四、解答题(本大题共3小题,每小题8分,共24分)
-
18. 随着教育信息化的不断推进,网络学习逐渐成为了学生课余学习的主要方式之一.梁老师为了解某校学生课余网络学习的情况,随机调查了部分学生一周课余网络学习时长的情况,绘制了以下不完整的频数分布表和扇形统计图.
组别
学习时长成t/小时
人数
A
8
B
16
C
a
D
b
E
12

根据以上信息解答下列问题.
(1)、此次调查共抽取了多少名学生?(2)、C组、D组的学生各有多少人?(3)、若该校共有2000名学生,估计该校一周课余网络学习时长不少于4.5小时的学生人数.19. 如图(1)所示的健身器械为倒蹬机,使用方法为上身不动,腿部向前发力,双腿伸直之后再慢慢收回.图(2)为其抽象示意图,已知在初始位置, , 点在同一直线上, , . (1)、当在初始位置时,求点到的距离;(2)、当双腿伸直后,点分别从初始位置运动到点 , 假设 , 三点共线,求此时点上升的竖直高度.(结果保留整数,参考数据: , , , , , )20. 如图,在中, , 以为直径的分别交于点 , 点在的延长线上,且 , 延长交的切线于点 , 过点作于点 , 交于点 , 连接 .
(1)、当在初始位置时,求点到的距离;(2)、当双腿伸直后,点分别从初始位置运动到点 , 假设 , 三点共线,求此时点上升的竖直高度.(结果保留整数,参考数据: , , , , , )20. 如图,在中, , 以为直径的分别交于点 , 点在的延长线上,且 , 延长交的切线于点 , 过点作于点 , 交于点 , 连接 . (1)、求证:为的切线;(2)、若 , , 求的长度.
(1)、求证:为的切线;(2)、若 , , 求的长度.五、解答题(本大题共2小题,每小题9分,共18分)
-
21. 如图(1),点分别是菱形的边上的动点,且的长为定值,小杰同学根据学习函数的经验,对的周长进行了探究,下面是小杰的探究过程.
 (1)、对于点在不同位置时,利用数学作图软件进行度量,得到了线段 , 的长度和的周长的几组对应值,如下表:
(1)、对于点在不同位置时,利用数学作图软件进行度量,得到了线段 , 的长度和的周长的几组对应值,如下表:位置1
位置2
位置3
位置4
位置5
位置6
位置7
位置8
0.00
1.07
2.00
2.50
2.99
3.99
5.00
6.00
5.35
4.90
4.72
4.59
4.48
4.91
4.91
4.51
4.60
4.74
5.11
5.55
6.00
的周长
15.86
15.41
15.32
15.33
15.59
16.14
16.91
请补全表格,并回答问题:
①的固定值是多少;
②在线段的长度这三个量中, ▲ 的长度是自变量 , 的周长是这个自变量的函数.
(2)、在图(2)中的平面直角坐标系中,画出(1)中所确定的函数的大致图象.(3)、解决问题:的周长的最小值约为 . (结果保留一位小数)22. 已知在中, , 点D为边上一动点,以为边,在的右侧作等边三角形 . (1)、如图(1),当平分时,四边形是形.(2)、如图(2),过点E作于点F , 与具有怎样的关系?F为的中点吗?说明理由.可得出结论,无论运动到何处,点E在的何处?(3)、如图(3),若 , 利用(2)中结论.
(1)、如图(1),当平分时,四边形是形.(2)、如图(2),过点E作于点F , 与具有怎样的关系?F为的中点吗?说明理由.可得出结论,无论运动到何处,点E在的何处?(3)、如图(3),若 , 利用(2)中结论.①当D为的中点时,过点E作于点G , 求的长;
②点D从点B运动到点C , 则点E所经过的路径长为多少?
六、(本大题共12分)
-
23. 已知二次函数的图象( 记为抛物线) 顶点为M,直线:y=2x-a与x轴,y轴分别交于点A,B.
 (1)、若抛物线与x轴只有一个公共点,求a的值;(2)、当a>0时,设△ABM的面积为S,求S与a的函数关系式;(3)、将二次函数的图象绕点P(t,-2)旋转180°得到二次函数的图象记为抛物线 , 顶点为N.
(1)、若抛物线与x轴只有一个公共点,求a的值;(2)、当a>0时,设△ABM的面积为S,求S与a的函数关系式;(3)、将二次函数的图象绕点P(t,-2)旋转180°得到二次函数的图象记为抛物线 , 顶点为N.①若点N恰好落在直线上,求a 与t 满足的关系;
②当-2≤x≤1时,旋转前后的两个二次函数y的值都会随x的值得增大而减小,求t 的取值范围.