江西省赣州市瑞金市2023-2024学年八年级下学期数学期中试卷-在线组卷题库

1. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{20}$ B、 $\sqrt{2}$ C、 $\sqrt{\frac{1}{2}}$ D、 $\sqrt{0.2}$

查看试题解析
2. 下列各组线段，能组成直角三角形的是（）

A、 $a = 1$ ， $b = 2$ ， $c = 2$ B、 $a = 2$ ， $b = 3$ ， $c = 5$ C、 $a = 2$ ， $b = 4$ ， $c = 5$ D、 $a = 3$ ， $b = 4$ ， $c = 5$

查看试题解析
3. 如图，四边形ABCD的对角线交于点O ，下列哪组条件不能判断四边形ABCD是平行四边形（）

A、OA＝OC ， OB＝OD B、AB＝CD ， AO＝CO C、AB＝CD ， AD＝BC D、∠BAD＝∠BCD ， AB∥CD

查看试题解析
4. 用四张一样大小的长方形纸片拼成一个如图所示的正方形 $A B C D$ ，它的面积是75， $A E = 3 \sqrt{3}$ ，图中空白的地方是一个正方形，那么这个小正方形的周长为（）

A、 $2 \sqrt{3}$ B、 $4 \sqrt{3}$ C、 $5 \sqrt{3}$ D、 $6 \sqrt{3}$

查看试题解析
5. 如图，一架2.5米长的梯子 $A B$ 斜靠在墙 $A C$ 上，这时梯足B到墙底端C的距离为0.7米，如果梯子的顶端沿墙垂直下滑0.4米，那么梯足将外移的长度是（）

A、0.7米 B、0.4米 C、0.8米 D、1米

查看试题解析
6. 如图， $△ A B C$ 中， $A D$ 是中线， $A E$ 是角平分线， $C F ⊥ A E$ 于F ， $A B = 13$ ， $A C = 8$ ，则 $D F$ 的长为（）

A、3 B、1.5 C、2 D、2.5

查看试题解析

7. 使 $\sqrt{x + 1}$ 有意义的x的取值范围是．

查看试题解析
8. 如图所示，四边形 $A B C D$ 是平行四边形，点E在线段 $B C$ 的延长线上，若 $∠ D C E = 132 °$ ，则 $∠ A =$ ．

查看试题解析
9. 计算： ${(\sqrt{3} + 1)}^{2} + {(\sqrt{3} - 1)}^{2} =$ ．

查看试题解析
10. 如图，在平行四边形 $A B C D$ 中对角线 $A C$ 、 $B D$ 相交于点O ， $∠ B A C = 90 °$ ， $A B = 3$ ， $B C = 5$ ，则 $B D =$ ．

查看试题解析
11. 如图，某风景区的沿湖公路AB=3千米，BC=4千米，CD=12千米，AD=13千米，其中AB⊥BC ，图中阴影是草地，其余是水面．那么乘游艇游点C出发，行进速度为每小时11 $\frac{7}{13}$ 千米，到达对岸AD最少要用小时．

查看试题解析
12. 在△ABC 中，∠A=30°，∠B=90°，AC=8，点 D 在边 AB，且 BD= $\sqrt{3}$ ，点 P 是△ABC 边上的一个动点，若 AP=2PD 时，则 PD的长是．

查看试题解析

13. 计算：

(1)、 $5 \sqrt{2} + \sqrt{8} - 7 \sqrt{18}$

(2)、如图，在平行四边形 $A B C D$ 中，点E、F分别在 $A D 、 B C$ 上，且 $A E = C F$ ，求证：四边形 $B F D E$ 是平行四边形

查看试题解析
14. 有一块矩形木板，木工采用如图的方式，在木板上截出两个面积分别为 $18 d m^{2}$ 和 $32 d m^{2}$ 的正方形木板.

(1)、截出的两块正方形木料的边长分别为， .

(2)、求剩余木料的面积.

查看试题解析
15. 如图，有一张四边形纸片 $A B C D$ ， $A B ⊥ B C$ ．经测得 $A B = 9 c m$ ， $B C = 12 c m$ ， $C D = 8 c m$ ， $A D = 17 c m$ ．

(1)、求 $A$ 、 $C$ 两点之间的距离．

(2)、求这张纸片的面积．

查看试题解析
16. 已知四边形ABCD是平行四边形，BD为对角线，分别在图①、图②中按要求作图（保留作图痕迹，不写作法）．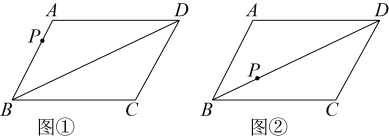

(1)、如图①，点P为AB上任意一点，请仅用无刻度的直尺在CD上找出另一点Q，使AP＝CQ；

(2)、如图②，点P为BD上任意一点，请仅用无刻度的直尺在BD上找出一点Q，使BP＝DQ．

查看试题解析
17. 如图所示，在 $▱ A B C D$ 中，点 $E$ 是 $A D$ 中点，连接 $B E$ 并延长，交 $C D$ 的延长线于点 $F$ ．

(1)、求证： $△ A B E ≌ △ D F E$ ．

(2)、连接 $C E$ ，若 $B E$ 平分 $∠ A B C$ ，且当 $B F = 8 c m, B C = 5 c m$ 时，求 $E C$ 的长．

查看试题解析

18. 如图， $▱ A B C D$ 的对角线 $A C 、 B D$ 相交于点O ，且E、F、G、H分别是 $A O 、 B O 、 C O 、 D O$ 的中点．

(1)、求证：四边形 $E F G H$ 是平行四边形；

(2)、若 $A C + B D = 42 ， A B = 14$ ，求 $△ O E F$ 的周长．

查看试题解析
19.

(1)、课本再现：
如图1，四个全等的直角三角形拼成一个大正方形，中间空白部分也是正方形．已知直角三角形的两直角边长分别为a ， b ，斜边长为c ．课堂上，老师结合图形，用不同的方式表示大正方形的面积，证明了勾股定理，请证明： $a^{2} + b^{2} = c^{2}$ ．

(2)、类比迁移：现将图1中的两个直角三角形向内翻折，得到图2，若 $a = 3$ ， $b = 4$ ，求空白部分的面积．

查看试题解析
20. 秦九韶（1208年~1268年），字道古，南宋著名数学家．与李冶、杨辉、朱世杰并称宋元数学四大家，他精研星象、音律、算术、诗词、弓剑、营造之学，他于1247年完成的著作《数学九章》中关于三角形的面积公式与古希腊几何学家海伦的成果并称“海伦−秦九韶公式”，它的主要内容是，如果一个三角形的三边长分别是a ， b ， c ，记 $p = \frac{a + b + c}{2}$ ， S为三角形的面积，那么 $S = \sqrt{p (p - a) (p - b) (p - c)}$ ．

(1)、如图在 $△ A B C$ 中， $B C = 5$ ， $A C = 6$ ， $A B = 7$ ，请用上面的公式计算 $△ A B C$ 的面积；

(2)、一个三角形的三边长分别为a ， b ， c ， $s = p = 15$ ， $a = 10$ ，求 $b c$ 的值，

查看试题解析

21. 如图所示，四边形 $A B C D$ 是平行四边形， $∠ B A D$ 的角平分线 $A E$ 交 $C D$ 于点F ，交 $B C$ 的延长线于点E ．

(1)、求证： $B E = C D$ ；

(2)、若 $B F$ 恰好平分 $∠ A B E$ ，连接 $A C 、 D E$ ，求证：四边形 $A C E D$ 是平行四边形；

(3)、若 $B F ⊥ A E$ ， $∠ B E A = 60 °$ ， $A B = 4$ ，求平行四边形 $A B C D$ 的面积．

查看试题解析
22. 定义：我们将 $(\sqrt{a} + \sqrt{b})$ 与 $(\sqrt{a} - \sqrt{b})$ 称为一对“对偶式”．因为 $(\sqrt{a} + \sqrt{b}) (\sqrt{a} - \sqrt{b}) = {(\sqrt{a})}^{2} - {(\sqrt{b})}^{2} = a - b$ ，可以有效的去掉根号，所以有一些问题可以通过构造“对偶式”来解决．
例如：已知 $\sqrt{18 - x} - \sqrt{11 - x} = 1$ ，求 $\sqrt{18 - x} + \sqrt{11 - x}$ 的值，可以这样解答：
因为 $(\sqrt{18 - x} - \sqrt{11 - x}) \times (\sqrt{18 - x} + \sqrt{11 - x}) = {(\sqrt{18 - x})}^{2} - {(\sqrt{11 - x})}^{2} = 18 - x - 11 + x = 7$ ，
所以 $\sqrt{18 - x} + \sqrt{11 - x} = 7$ ．

(1)、已知： $\sqrt{20 - x} + \sqrt{4 - x} = 8$ ，求 $\sqrt{20 - x} - \sqrt{4 - x}$ 的值；

(2)、结合已知条件和第①问的结果，解方程： $\sqrt{20 - x} + \sqrt{4 - x} = 8$ ；

(3)、计算： $\frac{1}{3 \sqrt{1} + \sqrt{3}} + \frac{1}{5 \sqrt{3} + 3 \sqrt{5}} + \frac{1}{7 \sqrt{5} + 5 \sqrt{7}} + \cdot \cdot \cdot + \frac{1}{2023 \sqrt{2021} + 2021 \sqrt{2023}}$ ．

查看试题解析

23. 综合与实践；
【问题情境】为了研究折纸过程中蕴涵的数学知识，老师发给每位同学完全相同的纸片，纸片形状如图1，在四边形 $A B C D$ 中（ $B C \geq C D$ ）， $A B ∥ C D$ ， $∠ B = 90 °$ ．
【探究实践】
老师引导同学们在边 $B C$ 上任取一点E ，连接 $D E$ ，将 $△ D C E$ 沿 $D E$ 翻折，点C的对应点为H ，然后将纸片展平，连接 $C H$ 并延长，分别交 $D E$ ， $A B$ 于点M ， G ．老师让同学们探究：当点E在不同位置时，能有哪些发现？经过思考和讨论，小莹、小明向同学们分享了自己的发现．

(1)、如图2，小莹发现：“当折痕 $D E$ 与 $A D$ 夹角为 $90 °$ 时，则四边形 $A G C D$ 是平行四边形”．请你判断小莹的结论是否正确，并说明理由．

(2)、如图3，小明发现：“当E是 $B C$ 的中点时，延长 $D H$ 交 $A B$ 于点N ，连接 $E N$ ，则N是 $B G$ 的中点”，请你判断小明的结论是否正确，并说明理由．

(3)、【拓展应用】
如图4，小慧在小明发现的基础上，经过进一步思考发现：“延长 $E H$ 交 $A B$ 于点F ．当给出 $B C$ 和 $B F$ 的长时，就可以求出 $C D$ 的长”．老师肯定了小慧同学结论的正确性．若 $B C = 6$ ， $B F = 4$ ，请你帮小慧求出 $C D$ 的长．

查看试题解析

江西省赣州市瑞金市2023-2024学年八年级下学期数学期中试卷

一、选择题（本大题共6小题，每小题3分，共18分，每小题只有一个正确选项．）

二、填空题（本大题共6小题，每小题3分，共18分）

三、（本大题共5小题，每小题6分，共30分）

四、（本大题共3小题，每小题8分，共24分）

五、（本大题共2小题，每小题9分，共18分）

六、（本大题共12分）