江西省景德镇市乐平市2023-2024学年七年级下学期数学期中试题

试卷更新日期：2024-06-13 类型：期中考试

进入出卷网下载

一、单项选择题（本大题共有6小题，每题3分，共18分．）

1. 下列运算正确的是（）

A、a²•a³=a⁶ B、（﹣a²）³=﹣a⁵ C、a¹⁰÷a⁹=a（a≠0） D、（﹣bc）⁴÷（﹣bc）²=﹣b²c²

查看试题解析
2. 如图，下列结论正确的是（）

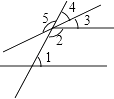A、∠5与∠2是对顶角 B、∠1与∠3是同位角 C、∠2与∠3是同旁内角 D、∠1与∠2是同旁内角

查看试题解析
3. 如图，已知直线 $A B ∥ C D$ ， $E G$ 平分 $∠ B E F$ ， $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数是（）

A、 $70 °$ B、 $50 °$ C、 $40 °$ D、 $140 °$

查看试题解析
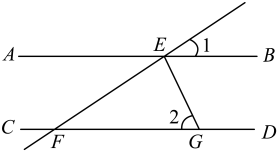4. 如图所示，下列判断错误的是（）

A、若∠1＝∠3，AD∥BC，则BD是∠ABC的平分线 B、若AD∥BC，则∠1＝∠2＝∠3 C、若∠3+∠4+∠C＝180°，则AD∥BC D、若∠2＝∠3，则AD∥BC

查看试题解析
5. 如图，点C在∠AOB的边OB上，用尺规作出了∠BCN=∠AOC，作图痕迹中，弧FG是（）

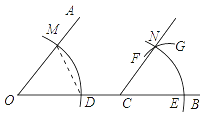A、以点C为圆心，OD为半径的弧 B、以点C为圆心，DM为半径的弧 C、以点E为圆心，OD为半径的弧 D、以点E为圆心，DM为半径的弧

查看试题解析
6. 小明根据邻居家的故事写了一首小诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还．”如果用纵轴y表示父亲与儿子行进中离家的距离，用横轴x表示父亲离家的时间，那么下面的图象与上述诗的含义大致吻合的是（）

A、 B、 C、 D、

查看试题解析

二、填空题（本大题有6小题，每小题3分，共18分．）

7. 若m、n满足 $3 m - n - 4 = 0$ ，则 $8^{m} \div 2^{n} =$ ．

查看试题解析
8. 已知 $y^{2} - m y + 1$ 是完全平方式，则 $m$ 的值是．

查看试题解析
9. 计算： $(- 1)^{2024} + (π - 3.14)^{0} - {(\frac{1}{2})}^{- 2} =$ .

查看试题解析
10. 某颗粒物的直径是0.000000071，把0.000000071用科学记数法表示为．

查看试题解析
11. 如图， $A B ∥ C D ， B C ∥ E D ， ∠ B = 80 °$ ，则 $∠ D =$ 度．

查看试题解析
12. 已知王强家、体育场、学校在同一直线上，下面的图像反映的过程是：某天早晨，王强从家跑步去体育场锻炼，锻炼结束后，步行回家吃早餐，饭后骑自行车到学校．图中 $x$ 表示时间， $y$ 表示王强离家的距离．则下列结论正确的是．（填写所有正确结论的序号）
①体育场离王强家 $2.5 k m$
②王强在体育场锻炼了 $30 m i n$
③王强吃早餐用了 $20 m i n$
④王强骑自行车的平均速度是 $0.2 k m / m i n$

查看试题解析

三、解答题．（本大题有5小题，每小题6分，共30分）

13.

(1)、 $(x + 3)^{2} - (x - 1) (x - 2)$

(2)、 $50 0^{2} - 499 \times 501$ （用简便方法计算）

查看试题解析
14. 先化简，再求值： $(a + 3) (a - 2) - a (a - 1)$ ，其中 $a = 8$ .

查看试题解析
15. 已知某长方形的面积是 $6 a^{2} - 8 a b + 2 a$ ，它的一边长为 $2 a$ ，求此长方形的周长.

查看试题解析
16. 如图，点 $A$ 、 $B$ 、 $C$ 、 $D$ 在一条直线上， $C E$ 与 $B F$ 交于点 $G$ ， $∠ A = ∠ 1$ ， $C E ∥ D F$ ，求证： $∠ E = ∠ F$

查看试题解析
17. 草莓销售季节，某种植基地开发了草莓采摘无人销售方式，为方便小朋友体验，销售人员把销售的草莓数量x（kg）与销售总价y（元）之间的关系写在了下列表格中：
销售数量x（kg）
1
2
3
4
…
销售总价y（元）
8.5
16.5
24.5
32.5
…

(1)、请你写出草莓的销售数量x（kg）与销售总价y（元）之间的关系式；

(2)、丽丽一家共摘了6.5kg草莓，应付多少钱？

查看试题解析

四、解答题．（本大题有3小题，每小题8分，共24分）

18. 若a、b可以代表一个数或一个代数式，定义运算“◎”如下： $a ◎ b = (a + b)^{2} - (a - b)^{2}$

(1)、化简：（2m）◎（3n）；

(2)、若 $(m + 2) ◎ (m - 3) = 4 m^{2}$ ，求m ．

查看试题解析
19. 填写下面解题过程中的推理依据：如图， $A B ∥ C D$ ， $B E$ 平分 $∠ A B C$ ， $C F$ 平分 $∠ B C D$ ．

(1)、 $∠ 1 = ∠ 2$ 吗？请说明理由．
解： $∠ 1 = ∠ 2$ ，理由如下：
因为 $A B ∥ C D$ （已知），
所以 $∠ A B C = ∠ B C D$ （）．
因为 $B E$ 平分 $∠ A B C$ ， $C F$ 平分 $∠ B C D$ （已知），
所以 $∠ 1 = \frac{1}{2} ∠$ （角平分线的定义）， $∠ 2 = \frac{1}{2} ∠$ （角平分线的定义），
所以 $∠ 1 = ∠ 2$ （）．

(2)、 $B E$ 与 $C F$ 的位置关系如何？为什么？

查看试题解析
20. 泰和工农兵大道安装的护栏平面示意图如图所示，假如每根立柱宽为0.2米，立柱间距为3米．

(1)、根据上图，将表格补充完整．
立柱根数
1
2
3
4
5
……
护栏总长度（米）
0.2
3.4
__
9.8
__
……

(2)、在这个变化过程中，自变量、因变量各是什么？

(3)、设有x根立柱，护栏总长度为y米，则y与x之间的关系式是什么？

(4)、求护栏总长度为61米时立柱的根数？

查看试题解析

五、解答题．（本大题有2小题，每小题9分，共18分）

21. 如图①是一个长为 $2 m$ 、宽为 $2 n$ 的长方形，沿图中虚线用剪刀均分成四块小长方形，然后按图②的形状拼成一个正方形.

(1)、请用两种不同的方法表示图②中阴影部分的面积（结果不化简）.
方法1：；方法2：.

(2)、观察图②，请写出 $(m + n)^{2}$ ， $(m - n)^{2}$ ， $m n$ 三个式子之间的等量关系；

(3)、根据（2）题中的等量关系，解决如下问题：已知 $a + b = 7$ ， $a b = 5$ ，求 $(a - b)^{2}$ 的值.

查看试题解析
22. 如图1，以直线 $A B$ 上一点O为端点作射线 $O C$ ，使 $∠ B O C = 75 °$ ．将一个直角三角板 $D O E$ 的直角顶点O放在直线 $A B$ 上的点O处，边 $O D$ 放在射线 $O B$ 上．

(1)、 $∠ C O E =$ ；

(2)、如图2，将直角三角板 $D O E$ 绕点O按逆时针方向转动，当射线 $O C$ 恰好平分 $∠ B O E$ 时，求 $∠ C O D$ 的度数；

(3)、如图3，将直角三角板 $D O E$ 绕点O转动，如果 $O D$ 始终在 $∠ B O C$ 的内部，试猜想 $∠ B O D$ 和 $∠ C O E$ 有怎样的数量关系，并说明理由．

查看试题解析

六、解答题．（本大题12分）

23. 求解下列各题

(1)、如图（1）， $A B ∥ C D$ ，点 $P$ 在 $A B 、 C D$ 外部，若 $∠ B = 40 °, ∠ D = 15 °$ ，则 $∠ B P D =$ $°$

(2)、如图（2）， $A B ∥ C D$ ，点 $P$ 在 $A B 、 C D$ 内部，则 $∠ B, ∠ B P D, ∠ D$ 之间有何数量关系？证明你的结论；

(3)、在图（2）中，将直线 $A B$ 绕点 $B$ 按逆时针方向旋转一定角度交直线 $C D$ 于点 $M$ ，如图（3），若 $∠ B P D = 90 °, ∠ B M D = 40 °$ ，求 $∠ B + ∠ D$ 的度数．

查看试题解析