湖北省黄石市2023-2024学年七年级下学期数学期中试题

试卷更新日期：2024-06-13 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共30分）

1. 9的平方根是（）

A、3 B、 $\sqrt{3}$ C、±3 D、 $\pm \sqrt{3}$

查看试题解析
2. 如图，下列条件中，能判定a∥b的是（）

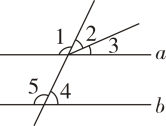A、∠1+∠4=180° B、∠2=∠4 C、∠1=∠4 D、∠5=∠2+∠3

查看试题解析
3. 已知点Q的坐标为 $(2, - 3)$ ，点P的坐标为 $(2 a + 2, a - 5)$ ，若直线 $P Q ⊥ y$ 轴，则点Р的坐标为（）

A、 $(2, - 5)$ B、 $(2, 2)$ C、 $(- 14, - 3)$ D、 $(6, - 3)$

查看试题解析
4. 下列说法正确的是（）

A、 $- a$ 一定没有平方根 B、25的平方根是 $\pm 5$ C、立方根等于它本身的数是0，1 D、－4的算数平方根是2

查看试题解析
5. 如图，下列5种说法：① $∠ 1$ 与 $∠ 4$ 是内错角；② $∠ 1$ 与 $∠ 2$ 是同位角；③ $∠ 4$ 与 $∠ 5$ 是同旁内角；④ $∠ 2$ 与 $∠ 4$ 是同位角；⑤∠2与∠5是内错角．其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，将周长为8 的△ABC沿BC 方向平移2个单位长度得到△DEF，则四边形 ABFD的周长为（）

A、10 B、12 C、14 D、16

查看试题解析
7. 按如图所示的程序计算，若开始输入的x的值是64，则输出的y的值是（）

A、 $\sqrt{2}$ B、 $\sqrt[3]{2}$ C、2 D、 $\sqrt[3]{4}$

查看试题解析
8. 如图，学校相对于小明家的位置下列描述最准确的是（）

A、距离学校1200米处 B、南偏西65°方向上的1200米处 C、北偏东65°方向上的1200米处 D、南偏西25°方向上的1200米处

查看试题解析
9. 下列说法：① $\sqrt{{(- 10)}^{2}} = - 10$ ﹔②无理数都是无限小数；③－3是 $\sqrt{81}$ 的平方根；④任何实数不是有理数就是无理数；⑤两个无理数的和还是无理数，正确的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 如图，已知 $A B ∥ E G$ ， $B C ∥ D E$ ， $C D ∥ E F$ ，则x ， y ， z三者之间的关系是（）

A、 $x + y + z = 180 °$ B、 $y - x = z$ C、 $y - x = x - z$ D、 $x - z = y$

查看试题解析

二、填空题（每小题3分，共15分）

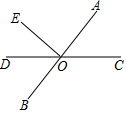
11. 在 $\frac{16}{3}$ ， $\sqrt{3}$ ， π ， 0，－1.6， $\sqrt{6}$ 中，无理数有个．

查看试题解析
12. 如图，直线AB和CD交于点O，EO⊥AB，垂足为O，∠AOD＝125°，则∠COE＝°．

查看试题解析
13. 如图，将某动物园中的猴山，狮虎山，熊猫馆分别记为M ， N ， P ，若建立平面直角坐标系，将猴山M ，狮虎山N用坐标分别表示为 $(2, 1)$ 和 $(8, 2)$ ，则熊猫馆Р用坐标表示为．

查看试题解析
14. 已知一个正数的两个平方根分别是 $2 a + 3$ 和 $6 - 5 a$ ，那么 $8 a + 3$ 的立方根是．

查看试题解析
15. 如图， $A E ∥ C F$ ， $∠ A C F$ 的平分线交AE于点B ， G是CF上的一点， $∠ G B E$ 的平分线交CF于点D ，且 $B D ⊥ B C$ ，下列结论：①BC平分 $∠ A B G$ ﹔② $A C ∥ B G$ ﹔③若 $∠ A = α$ ，则 $∠ B D F = 180 ° - \frac{α}{2}$ ；④与 $∠ D B E$ 互余的角有2个，其中正确的有．（把你认为正确结论的序号都填上）

查看试题解析

三、解答题（共75分）

16. 计算或解方程

(1)、计算： $| \sqrt{3} - 2 | + \sqrt{9} + \sqrt[3]{- 27}$ ；

(2)、解方程： ${(x - 1)}^{2} = 9$

查看试题解析
17. 已知 $5 a + 2$ 的立方根是3， $3 a + b - 1$ 的算术平方根是4，c是 $\sqrt{17}$ 的整数部分．求 $3 a - b + c$ 的平方根．

查看试题解析
18. 请将下面解答过程填写完整．
如图， $E F ∥ A D$ ， $∠ B A C = 75 °$ ，若 $∠ 1 = ∠ 2$ ，求 $∠ A G D$ 的度数．
解：∵ $E F ∥ A D$ （已知），
∴ $∠ 2 = ∠ 3$ （）．
∵ $∠ 1 = ∠ 2$ （已知），
∴ $∠ 1 =$     ▲    （等量代换）．
∴ $A B ∥$     ▲
∴    ▲     $+ ∠ B A C = 180 °$ （）．
∵ $∠ B A C = 75 °$ （已知），
∴ $∠ A G D =$     ▲

查看试题解析
19. 已知点 $P (- 3 a - 4, 2 + a)$ ，解答下列各题：

(1)、若点P在x轴上，则点P的坐标为；

(2)、若点P在第二象限，且它到x轴、y轴的距离相等，求 $a^{2023} + 2024$ 的值．

查看试题解析
20. 如图，点O是直线AB上一点，射线OC，OD，OE在直线AB的同一侧，且OC平分∠AOE，OD⊥OC．

(1)、如果∠COE=40°，求∠AOD的度数．

(2)、如果∠AOE+30°=∠BOE，求∠BOD的度数．

查看试题解析
21. 如图，已知 $C D ∥ B E$ ， $∠ 1 + ∠ 2 = 180 °$ ．

(1)、试问 $∠ A F E$ 与 $∠ A B C$ 相等吗？请说明理由；

(2)、若 $∠ D = 2 ∠ A E F$ ， $∠ 1 = 136 °$ ，求D的度数．

查看试题解析
22. 如图，在平面直角坐标系xOy中， $A (5, 3)$ ， $B (3, 1)$ ， $C (1, 2)$ ．将三角形ABC向左平移5个单位长度，再向上平移3个单位长度，可以得到三角形 $A_{1} B_{1} C_{1}$ ，其中点 $A_{1}$ ， $B_{1}$ ， $C_{1}$ ，分别与点A ， B ， C对应．

(1)、画出平移后的三角形 $A_{1} B_{1} C_{1}$ ；

(2)、求三角形 $A_{1} B_{1} C_{1}$ 的面积；

(3)、若点P在y轴上，以 $A_{1}$ ， $B_{1}$ ， P为顶点的三角形面积为2，求点P的坐标．

查看试题解析
23. 大家知道 $\sqrt{2}$ 是无理数，而无理数是无限不循环小数，因此 $\sqrt{2}$ 的小数部分我们不可能全部写出来，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分，你同意小明的表示方法吗？
事实上，小明的表示方法有道理、因为 $\sqrt{2}$ 的整数部分是1，将 $\sqrt{2}$ 减去其整数部分，差就是小数部分．
又例如：因为 $4 < 7 < 9$ ，即 $2 < \sqrt{7} < 3$ ，所以 $\sqrt{7}$ 的整数部分为2，小数部分为 $\sqrt{7} - 2$ ．
根据以上内容，解答下列问题：

(1)、 $\sqrt{17}$ 的整数部分是，小数部分是；

(2)、如果 $\sqrt{5}$ 的小数部分为a ， $\sqrt{13}$ 的整数部分为b ，求 $a + b - \sqrt{5}$ 的值；

(3)、已知 $10 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 < y < 1$ ，求 $x - y$ 的值．

查看试题解析
24. 如图，已知直线 $A B ∥ C D$ ， $∠ A = ∠ C = 108 °$ ，点E ， F在CD上，且满 $∠ D B F = ∠ A B D$ ， BE平分 $∠ C B F$ ．

(1)、直线AD与BC有何位置关系？请说明理由；

(2)、求 $∠ D B E$ 的度数；

(3)、若左右平移AD ，在平移AD的过程中，
①求 $∠ B F C$ 与 $∠ B D C$ 的数量关系
②是否存在某种情况，使 $∠ B E C = ∠ A D B$ ，若存在，求出 $∠ A D B$ 的度数；若不存在，请说明理由．

查看试题解析