江西省上饶市婺源县2023-2024学年七年级下学期数学期中试题
试卷更新日期:2024-06-13 类型:期中考试
一、选择题:本题共8小题,每小题3分,共24分.
-
1. 下列图案中可以看作由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中,由AB∥CD , 能得到∠1=∠2的是( )A、
2. 下列图形中,由AB∥CD , 能得到∠1=∠2的是( )A、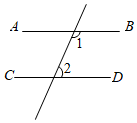 B、
B、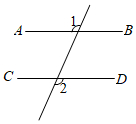 C、
C、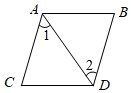 D、
D、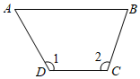 3. 的平方根等于( )A、 B、 C、 D、4. 在平面直角坐标系的第四象限内有一点 , 到轴的距离为4,到轴的距离为5,则点的坐标为( )A、 B、 C、 D、5. 在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是 和﹣1,则点C所对应的实数是( )
3. 的平方根等于( )A、 B、 C、 D、4. 在平面直角坐标系的第四象限内有一点 , 到轴的距离为4,到轴的距离为5,则点的坐标为( )A、 B、 C、 D、5. 在如图所示的数轴上,点B与点C关于点A对称,A,B两点对应的实数分别是 和﹣1,则点C所对应的实数是( ) A、1+ B、2+ C、2 ﹣1 D、2 +16. 下列说法正确的有( )
A、1+ B、2+ C、2 ﹣1 D、2 +16. 下列说法正确的有( )①内错角相等;②点到直线的垂线段叫做点到直线的距离;③两个无理数的和还是无理数;④两点之间,线段最短;⑤如果一个实数的立方根等于他本身,这个数只有0或1;⑥在同一平面内,若两条直线都与第三条直线垂直,那么这两条直线互相平行.
A、1个 B、2个 C、3个 D、4个7. 我国古代数学著作《增删算法统宗》记载”绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托“其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长x尺,竿长y尺,则符合题意的方程组是( )A、 B、 C、 D、8. 如图,矩形的各边分别平行于轴或轴,甲乙分别由点同时出发,沿矩形的边作环绕运动甲按逆时针方向以个单位/秒的速度匀速运动,乙按顺时针方向以个单位/秒的速度匀速运动,则甲、乙运动后的第次相遇地点的坐标是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共8小题,每小题3分,共24分.
-
9. 如图,想在河的两岸搭建一座桥,搭建方式最短的是 , 理由是 .
 10. 若 与互为相反数,则 .11. 比较实数大小:(填“>”或“<”).12. 如图,在平面直角坐标系中,的顶点A , B的坐标分别是 , . 平移得到 , 若点的对应点的坐标为 , 则点的对应点的坐标是 .
10. 若 与互为相反数,则 .11. 比较实数大小:(填“>”或“<”).12. 如图,在平面直角坐标系中,的顶点A , B的坐标分别是 , . 平移得到 , 若点的对应点的坐标为 , 则点的对应点的坐标是 . 13. 用1块A型钢板可制成4件甲种产品和1件乙种产品;用1块B型钢板可制成3件甲种产品和2件乙种产品;要生产甲种产品37件,乙种产品18件,则恰好需用A、B两种型号的钢板共块.14. 已知点P(2a-6,a+1),若点P在坐标轴上,则点P的坐标为.15. 定义运算“*”,规定 ,其中 为常数,且 ,则 = .16. 如图,直线MN分别与直线AB,CD相交于点E,F,EG平分 , 交直线CD于点G,若 , 射线于点G,则.
13. 用1块A型钢板可制成4件甲种产品和1件乙种产品;用1块B型钢板可制成3件甲种产品和2件乙种产品;要生产甲种产品37件,乙种产品18件,则恰好需用A、B两种型号的钢板共块.14. 已知点P(2a-6,a+1),若点P在坐标轴上,则点P的坐标为.15. 定义运算“*”,规定 ,其中 为常数,且 ,则 = .16. 如图,直线MN分别与直线AB,CD相交于点E,F,EG平分 , 交直线CD于点G,若 , 射线于点G,则.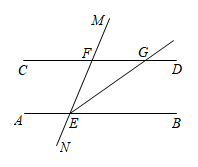
三、解答题:本题共7小题,共52分.
-
17. 计算:18. 解方程组19. 如图,在四边形中,射线平分交的延长线于点 , 且 , . 试猜想与的位置关系,并说明理由.
 20. 实数在数轴上的对应点的位置如图所示, .
20. 实数在数轴上的对应点的位置如图所示, . (1)、求的值;(2)、已知的小数部分是 , 的小数部分是 , 求的平方根.21. 如图,先将三角形向左平移个单位长度,再向下平移个单位长度,得到三角形 .
(1)、求的值;(2)、已知的小数部分是 , 的小数部分是 , 求的平方根.21. 如图,先将三角形向左平移个单位长度,再向下平移个单位长度,得到三角形 . (1)、画出三角形;(2)、求三角形的面积;(3)、设线段与轴的交点为 , 则点的坐标为 .22. 亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.(1)、计划调配36座新能源客车多少辆?该大学共有多少名志愿者?(2)、若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?23. 已知:直线 , 点M、N分别在直线、直线上,点E为平面内一点,
(1)、画出三角形;(2)、求三角形的面积;(3)、设线段与轴的交点为 , 则点的坐标为 .22. 亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.(1)、计划调配36座新能源客车多少辆?该大学共有多少名志愿者?(2)、若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?23. 已知:直线 , 点M、N分别在直线、直线上,点E为平面内一点, (1)、如图1,请写出 , , 之间的数量关系,并给出证明;(2)、如图2,利用(1)的结论解决问题,若 , 平分 , 平分 , , 求的度数;(3)、如图3,点G为上一点, , , 交于点H , , , 之间的数量关系(用含m的式子表示)是 .
(1)、如图1,请写出 , , 之间的数量关系,并给出证明;(2)、如图2,利用(1)的结论解决问题,若 , 平分 , 平分 , , 求的度数;(3)、如图3,点G为上一点, , , 交于点H , , , 之间的数量关系(用含m的式子表示)是 .