江西省抚州市南城县2023-2024学年八年级下学期数学期中试题

试卷更新日期：2024-06-13 类型：期中考试

进入出卷网下载

一、选择题（本大题共6小题，每小题3分，共18分．每小题只有一个正确选项）

1. 如图是我国几家银行的标志，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知三角形 $A B C$ 平移后得到三角形 $A^{'} B^{'} C^{'}$ ，且 $A^{'} (- 2, 3)$ ， $B^{'} (- 4, - 1)$ ， $C^{'} (m, n)$ ，已知 $C (m - 3, n - 2)$ ，则 $A$ ， $B$ 的原坐标分别为 $($ $)$

A、 $(1, 5)$ ， $(- 1, 1)$ B、 $(5, 1)$ ， $(1, - 3)$ C、 $(5, 0)$ ， $(- 1, 1)$ D、 $(- 5, 1)$ ， $(- 7, - 3)$

查看试题解析
3. 等腰三角形的一边长为4 cm，另一边长为9 cm，则它的周长为（）

A、13 cm B、17 cm C、22 cm D、17 cm或22 cm

查看试题解析
4. 在下列数学式子：① $- 2 < 0$ ， ② $2 x - 5 > 0$ ， ③ $b = 2$ ， ④ $x^{2} - x$ ， ⑤ $m \neq 3$ ， ⑥ $3 x + 2 y \geq 0$ 中，是不等式的有（　　）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 如果不等式组 ${\begin{array}{l} x > - 1 \\ x > a \end{array}$ 的解集是 $x > - 1$ ，那么a取值范围是（）

A、 $a > - 1$ B、 $a \geq - 1$ C、 $a \leq - 1$ D、 $a < - 1$

查看试题解析
6. 如图，在 $△ A B C$ ， $A H ⊥ B C$ ， $B F$ 平分 $∠ A B C$ ， $B E ⊥ B F$ ， $E F ∥ B C$ ，下列结论中： $① A H ⊥ E F$ ， $② ∠ A B F = ∠ E F B$ ， $③ ∠ E = ∠ A B E$ ， $④ A F = B E$ ．正确的是（）

A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

7. 若 $a < b$ ，那么 $- 4 a + 8$ $- 4 b + 8$ （填“>””<”或“=”）

查看试题解析
8. 若某三角形的三边长分别为 $5 ， 12 ， 13$ ，则该三角形的面积是．

查看试题解析
9. 如图，在 $△ A B C$ 中， $A B = A C = 15$ ， $A B$ 的垂直平分线 $D E$ 交 $A C$ 于D ，连接 $B D$ ，若 $△ D B C$ 的周长为27，则 $B C$ 的长为．

查看试题解析
10. 若Q为等边三角形 $A B C$ 内一点， $△ A B Q$ 绕点B旋转，使 $A B$ 与 $B C$ 边重合，则 $∠ Q B P =$

查看试题解析
11. 直线l₁：y＝x+1与直线l₂：y＝mx+n相交于点P（a，2），则关于x的不等式x+1≥mx+n的解集为．

查看试题解析
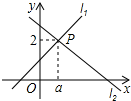12. 如图，∠AOB＝60°，点C是BO延长线上一点，OC＝6cm，动点P从点C出发沿射线CB以2cm/s的速度移动，动点Q从点O出发沿射线OA以1cm/s的速度移动，如果点P、Q同时出发，用t（s）表示移动的时间，当t＝s时，△POQ是等腰三角形．

查看试题解析

三、（本大题共5小题，每小题6分，共30分）

13.

(1)、解不等式 $3 x - 1 \geq 2 x + 4$ ，并把解集在数轴上表示出来．

(2)、如图， $O C$ 是 $∠ A O B$ 的平分线， $P D ⊥ O A$ 于点D ， $P D = 5$ ，则点P到 $O B$ 的距离是多少？

查看试题解析
14. 已知 $(b + 1) x^{| b + 1 |} < - 3$ 是关于x的一元一次不等式，试求b的值，并解这个一元一次不等式．

查看试题解析
15. 如图，将 $△ A B C$ 绕点B顺时针旋转 $80 °$ 到 $△ B D E$ 处，连接 $C E$ ，已知 $∠ A C B = 40 °$ ，求证： $∠ A C E = 90 °$ ．

查看试题解析
16. 如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点三角形 $A B C$ （顶点是网格线的交点）．

(1)、先将 $△ A B C$ 竖直向上平移6个单位，再水平向右平移3个单位得到 $△ A_{1} B_{1} C_{1}$ ，点A、B、C对应点分别是 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、将 $△ A_{1} B_{1} C_{1}$ 绕 $B_{1}$ 点顺时针旋转 $90 °$ ，得 $△ A_{2} B_{1} C_{2}$ ，点 $A_{1}$ 、 $C_{1}$ 对应点分别是 $A_{2}$ 、 $C_{2}$ ，请画出 $△ A_{2} B_{1} C_{2}$ ；

(3)、连接 $C A_{2}$ ，直接写出 $C A_{2}$ 的长．

查看试题解析
17. 如图， $∠ A = ∠ B = 90 °$ ， E是 $A B$ 上的一点，且 $A D = B E$ ， $∠ 1 = ∠ 2$ ，问： $△ A D E$ 与 $△ B E C$ 全等吗？请说明理由．

查看试题解析

四、（本大题共3小题，每小题8分，共24分）

18. 下面是小颖同学解一元一次不等式 $\frac{2 x + 1}{3} < \frac{x + 2}{6} + 2$ 的解答过程，请认真阅读并完成相应任务．
解：去分母得， $2 (2 x + 1) < x + 2 + 2$ $⋯$ 第 $①$ 步
去括号得， $4 x + 2 < x + 4$ $⋯$ 第 $②$ 步
移项得， $4 x - x < 4 - 2$ $⋯$ 第 $③$ 步
合并同类项得， $3 x < 2$ $⋯$ 第 $④$ 步
两边都除以 $3$ ，得 $x < \frac{2}{3}$ $⋯$ 第 $⑤$ 步
任务一：填空：

(1)、以上运算步骤中，第 $②$ 步去括号依据的运算律是；

(2)、任务二：请写出正确的解答过程．

查看试题解析
19. 等腰三角形一条腰上的中线将三角形的周长分成15和21两部分，求该三角形的腰长和底边的长.

查看试题解析
20. 某校九年级（21）班对半学期考试成绩优秀的学生进行奖励，颁发奖品，班主任安排生活委员到某文具店购买甲、乙两种奖品，若买甲种奖品20个，乙种奖品10个，共用110元，买甲种奖品30个比买乙种奖品20个少花10元．

(1)、求甲、乙两种奖品的单价各是多少元？

(2)、因奖品数量的需要和班费的限制，现要求本次购买甲种奖品的数量是乙种奖品的数量的2倍还少10个，而且购买这两种奖品的总金额不超过320元，请问最多购进乙种奖品多少个？

查看试题解析

五、（本大题共2小题，共18分）

21. 如图，△ABC是等边三角形，BD⊥AC，AE⊥BC，垂足分别为D、E，AE、BD相交于点O，连接DE．

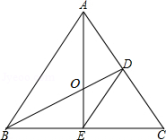(1)、判断△CDE的形状，并说明理由．

(2)、若AO＝12，求OE的长．

查看试题解析
22. 如图

(1)、课本再现
如图1， $∠ C A E$ 是 $△ A B C$ 的外角， $A D$ 平分 $∠ C A E$ ， $A D ∥ B C$ ，则 $A B$ $A C$ ．（填“>”“=”或“<”）

(2)、类比迁移
如图2，在 $△ A B C$ 中， $A D$ 是 $△ A B C$ 的一条角平分线，过点 $D$ 作 $D E ∥ A B$ 交 $A C$ 于点 $E$ ，求证： $A E = D E$ ．

(3)、拓展运用
如图3，在 $△ A B C$ 中， $A B = A C$ ， $O$ 是 $△ A B C$ 角平分线 $A D$ 上一点，延长 $B O$ 至点 $M$ ，使 $B O = O M$ ，过点 $M$ 作 $M N ∥ A B$ 交 $A C$ 于点 $N$ ，猜想 $M N$ 与 $N C$ 的数量关系，并进行证明．

查看试题解析

六、（本大题共12分）

23. 问题初探：数学课外兴趣小组活动时，数学杨老师提出了如下问题：在 $△ A B C$ 中， $A B = 7$ ， $A C = 3$ ，求 $B C$ 边上的中线 $A D$ 的取值范围．小明在组内经过合作交流，得到了如下的解决方法（如图1）：延长 $A D$ 到E ，使得 $D E = A D$ ；再连接 $B E$ ，把 $A B$ ， $A C$ ， $2 A D$ 集中在 $△ A B E$ 中；利用上述方法求出 $A D$ 的取值范围是 $2 < A D < 5$ ．

(1)、问题：请利用图1说明 $A C$ 与 $B E$ 的位置关系；
感悟：数学杨老师给学生们总结解这类问题时，条件中若出现“中点”“中线”等条件，可以考虑倍长中线，或通过引平行线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中．

(2)、类比分析：如图2， $△ A B C$ 和 $△ B D E$ 都是等腰直角三角形， $∠ A B C = ∠ D B E = 90 °$ ， $B F$ 是 $△ B E C$ 的中线，试探究线段 $A D$ 与 $B F$ 的数量和位置关系，并加以证明．

(3)、学以致用：如图3，已知 $△ A B C$ 为直角三角形， $∠ A C B = 90 °$ ， D为斜边 $A B$ 的中点，一个三角板的直角顶点与D重合，一个直角边 $D F$ 与 $A C$ 的延长线交于点F ，另一直角边与 $B C$ 边交于点E ，若 $A F = 12$ ， $B E = 5$ ，求出 $E F$ 的长是多少？

查看试题解析