湖北省武汉市东西湖区2023-2024学年七年级下学期数学期中试题

试卷更新日期：2024-06-13 类型：期中考试

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）下列各题中均有四个备选答案，其中有且只有一个正确，请在答卷上将正确答案的代号涂黑.

1. 在下列图形中， $∠ 1$ 与 $∠ 2$ 是对顶角的是（）

A、 B、 C、 D、

查看试题解析
2. 在平面直角坐标系中，点 $P (3, - 4)$ 位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 若 ${\begin{cases} x = 1 \\ y = 2 \end{cases}$ 是方程 $a x - 2 y = 4$ 的一个解，则a的值是（）

A、8 B、4 C、3 D、0

查看试题解析
4. 如图，直线 $A B$ ， $C D$ 相交于点O ， $E O ⊥ A B$ ，垂足为O ，若 $∠ E O C = 35 °$ ，则 $∠ A O D$ 的度数为（）

A、155° B、125° C、115° D、65°

查看试题解析
5. 东西湖区几处景点分布如图所示．若分别以正东、正北方向为x轴、y轴的正方向建立平面直角坐标系，表示极地海洋世界的点的坐标是 $(5, 3)$ ，表示五环体育中心的点的坐标是 $(- 6, 1)$ ，则表示园博园的点的坐标是（）

A、 $(2, 1)$ B、 $(3, 0)$ C、 $(3, - 1)$ D、 $(4, 0)$

查看试题解析
6. 在实数 $\frac{22}{7}$ 、3.14159265、 $\sqrt{7}$ 、 $- 8$ 、 $\sqrt[3]{2}$ 、0、 $\sqrt{36}$ 、 $\frac{π}{3}$ 中，无理数有（）个

A、1 B、2 C、3 D、4

查看试题解析
7. 光线在不同介质中的传播速度是不同的，因此光线从水中射向空气时，要发生折射．由于折射率相同，在水中平行的光线，在空气中也是平行的.如图是从玻璃杯底部发出的一束平行光线经过水面折射形成的光线示意图，水面与玻璃杯的底面平行.若 $∠ 1 = 45 °$ 、 $∠ 2 = 122 °$ ，则 $∠ 3 + ∠ 4$ 的大小是（）

A、167° B、103° C、93° D、90°

查看试题解析
8. 大约在1500年前，《孙子算经》中就记载了这个有趣的问题．书中是这样叙述的：今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何?这四句话的意思是：有若干只鸡兔同在一个笼子里，从上面数，有35个头，从下面数，有94只脚.问笼中各有多少只鸡和兔?设鸡有x只，兔有y只，列方程组得（）

A、 ${\begin{cases} x + y = 35 \\ 2 x + 4 y = 94 \end{cases}$ B、 ${\begin{cases} x + y = 35 \\ 2 x + 2 y = 94 \end{cases}$ C、 ${\begin{cases} x + y = 35 \\ x + 4 y = 94 \end{cases}$ D、 ${\begin{cases} x + y = 35 \\ 2 x + y = 94 \end{cases}$

查看试题解析
9. 若实数x满足 $0 < x < 1$ ，则x ， $x^{2}$ ， $\sqrt{x}$ 和 $\frac{1}{x}$ 的大小关系是（）

A、 $x^{2} < x < \sqrt{x} < \frac{1}{x}$ B、 $\frac{1}{x} < x < \sqrt{x} < x^{2}$ C、 $x < \sqrt{x} < x^{2} < \frac{1}{x}$ D、 $x^{2} < \sqrt{x} < x < \frac{1}{x}$

查看试题解析
10. 2024年2月，“顺遂安康龙腾盛世”长江主题灯光秀在武汉展演，两条笔直且平行的景观道 $M N$ 、 $P Q$ 上放置A、B两盏激光灯（如图所示）.A灯发出的光线自 $A M$ 按逆时针方向以每秒30°的速度旋转至 $A N$ 便立即回转，并不断往返旋转；B灯发出的光线自 $B P$ 按逆时针方向以每秒10°的速度旋转至 $B Q$ 就停止旋转.两灯不间断照射；B灯先转动2秒，A灯才开始转动，当两灯的光线互相平行时A灯旋转的时间是（）

A、1或6秒 B、8.5秒 C、3或6秒 D、1或8.5秒

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

11. $\sqrt{81}$ = ．

查看试题解析
12. 在方程 $2 x + y = 3$ 中，用含有x的式子表示y ，则 $y =$ .

查看试题解析
13. 点 $P (2, - 3)$ 到x轴的距离是个单位长度.

查看试题解析
14. 如图，将 $△ A B C$ 沿 $B C$ 方向平移到 $△ D E F$ 的位置，若 $B F = 10$ ， $E C = 2$ ，则线段 $A D =$ .

查看试题解析
15. 三个同学对问题“若方程组 ${\begin{cases} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{cases}$ 的解是 ${\begin{cases} x = - 1 \\ y = - 2 \end{cases}$ ，求方程组 ${\begin{cases} 5 a_{1} x + 6 b_{1} y = 7 c_{1} \\ 5 a_{2} x + 6 b_{2} y = 7 c_{2} \end{cases}$ 的解”提出各自的想法．甲说：“这个题目条件不够，不能求解”；乙说：“它们的系数有一定规律，可以试试”；丙说“能不能把第二个方程组的两个方程的两边都除以7，通过换元法来解决”．参考他们的讨论，该方程组的解是.

查看试题解析
16. 任何实数a ，可用 $[a]$ 表示不超过a的最大整数，如 $[4] = 4$ ， $[\sqrt{3}] = 1$ ，现对72进行如下操作： $72 \overset{第一次}{\to} [\sqrt{72}] = 8 \overset{第二次}{\to} [\sqrt{8}] = 2 \overset{第三次}{\to} [\sqrt{2}] = 1$ ，这样对72只需进行3次操作就能变为1．类似地，对81只需进行3次操作也能变为1，那么只需进行3次操作就能变为1的所有正整数中，最大的是.

查看试题解析

三、解答题（共8小题，共72分）

17. 计算或解方程

(1)、计算： $\sqrt{2} (\sqrt{2} + 2) - 2 \sqrt{2}$ ；

(2)、解方程： ${(x - 1)}^{3} = 64$

查看试题解析
18. 解下列二元一次方程组.

(1)、 ${\begin{cases} y = 2 x - 3 \\ 3 x + 2 y = 8 \end{cases}$

(2)、 ${\begin{cases} 3 x + 4 y = 2 \\ 2 x - y = 5 \end{cases}$

查看试题解析
19. 如图，在三角形ABC中，D是AB上一点，E是AC上一点，∠ADE=60°，∠B=60°，∠AED=40°；

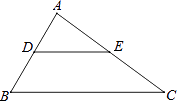(1)、求证：DE∥BC；

(2)、求∠C的度数．

查看试题解析
20. 如图， $A D ⊥ B C$ 于点D ， $E F ⊥ B C$ 于点F ，如果 $∠ 4 = ∠ C$ ，那么 $∠ 1$ 和 $∠ 2$ 相等吗?请阅读以下证明过程，并补全所空内容.
证明： $∠ 1 = ∠ 2$ ，理由如下.
$∵$ $A D ⊥ B C$ ， $E F ⊥ B C$ （已知）
$∴$ $∠ A D C = ∠$     ▲         $= 90 °$ （     ）
$∴$ $A D ∥ E F$ （     ）
$∴$ $∠ 1 = ∠$     ▲        （     ）
又 $∵$ $∠ 4 = ∠ C$ （已知）
$∴$ $A C ∥$     ▲        （同位角相等，两直线平行）
$∴$ $∠ 2 = ∠$     ▲        （     ）
$∴$ $∠ 1 = ∠ 2$ （等量代换）

查看试题解析
21. 如图，三角形 $A B C$ 中任意一点 $P (x_{0}, y_{0})$ 经平移后对应点为 $P_{1} (x_{0} + 4, y_{0} + 3)$ ，将三角形 $A B C$ 作同样的平移得到三角形 $A_{1} B_{1} C_{1}$

(1)、画出平移后的三角形 $A_{1} B_{1} C_{1}$ ，写出 $A_{1}$ ， $B_{1}$ ， $C_{1}$ 的坐标；

(2)、求三角形 $A_{1} B_{1} C_{1}$ 的面积；

(3)、若点M在y轴上，且三角形 $M B_{1} C_{1}$ 的面积等于三角形 $A_{1} B_{1} C_{1}$ 的面积，则点M的坐标为.

查看试题解析
22. 【问题背景】2台大收割机和5台小收割机同时工作2小时共收割小麦3.6公顷，3台大收割机和2台小收割机同时工作5小时共收割小麦8公顷.
【建立模型】设1台大收割机和1台小收割机每小时各收割小麦x公顷和y公顷.

(1)、用x ， y的式子表示2台大收割机和5台小收割机同时工作1h共收割小麦公顷；3台大收割机和2台小收割机同时工作1h共收割小麦公顷；

(2)、建立模型，解决实际问题.求1台大收割机和1台小收割机每小时各收割小麦多少公顷?

(3)、【方案决策】
随着天气的变化，为了“颗粒归仓”、“抢收抢种”，某乡镇准备引进上述型号的收割机若干台，每台收割机每天工作 $15 h$ ，连续工作20天，共收割小麦420公顷.为了完成任务，问有多少种引进收割机的方案.

查看试题解析
23. $A B ∥ C D$ ，点E、F分别在 $A B$ 、 $C D$ 上；点O在直线 $A B$ 、 $C D$ 之间，且 $∠ E O F = 80 °$ .

(1)、如图1，①若 $∠ O F C = 20 °$ ，求 $∠ A E O$ 的度数；
②若 $∠ O F C = α$ ，请你直接写出 $∠ O F C + ∠ A E O =$ ；

(2)、如图2，直线 $M N$ 分别交 $∠ B E O$ 、 $∠ O F C$ 的角平分线于点M、N ，求 $∠ E M N - ∠ F N M$ 的值.

(3)、如图3， $E G$ 在 $∠ A E O$ 内， $∠ A E G = m ∠ O E G$ ； $F H$ 在 $∠ D F O$ 内， $∠ D F H = m ∠ O F H$ ，直线 $M N$ 分别交 $E G$ 、 $F H$ 分别于点M、N ，且 $∠ F M N - ∠ E N M = 80 °$ ，直接写出m的值.

查看试题解析
24. 如图1，在平面直角坐标系中，将点 $A (- 1, 0)$ 向右平移4个单位得到点B ，将线段 $A B$ 向上平移m个单位，再向右移1个单位得到线段 $D C$ （点A与点D对应，点B与点C对应）且四边形 $A B C D$ 的面积为8.

(1)、直接写出m的值及点B ， C的坐标；

(2)、连接 $A C$ 与y轴交于点E ，求 $\frac{D E}{O E}$ 的值；

(3)、如图2，若点P从O点出发，以每秒n个单位的速度向上平移运动，同时点Q从B点出发，以每秒 $2 n$ 个单位的速度向左平移运动，当点P到达点D后停止运动.若射线 $C Q$ 交y轴于点F.设 $△ C F P$ 与 $△ O F Q$ 的面积差为S ，问：S是否为定值?如果S是定值，请求出它的值：如果S不是定值，请说明理由.

查看试题解析