江西省九江市重点校2023-2024学年八年级下学期数学期中试题

试卷更新日期：2024-06-13 类型：期中考试

进入出卷网下载

一、选择题（本题共计 12 小题，每题 3 分，共计36分）

1.
在6×6方格中，将图①中的图形N平移后位置如图②所示，则图形N的平移方法中，正确的是

图① 图②

A、向下移动1格 B、向上移动1格 C、向上移动2格 D、向下移动2格

查看试题解析
2. 如图，将 $△ A B C$ 绕着点 $C$ 按顺时针方向旋转 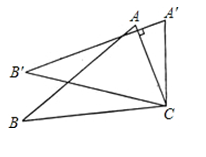$20 °$ ， $B$ 点落在 $B'$ 位置， $A$ 点落在 $A'$ 位置，若 $A C ⊥ A' B'$ ，则 $∠ B A C$ 的度数是（）

A、 $50 °$
B、 $60 °$
C、 $70 °$
D、 $80 °$

查看试题解析
3. 若不等式组 ${\begin{array}{l} \frac{x + 1}{3} < \frac{x}{2} - 1 \\ x < 4 m \end{array}$ 无解，则 $m$ 的取值范围为（）

A、 $m \leq 2$ B、 $m < 2$ C、 $m \geq 2$ D、 $m > 2$

查看试题解析
4. “x的2倍不小于3”用不等式表示是（）

A、 $2 x < 3$ B、 $2 x > 3$ C、 $2 x \leq 3$ D、 $2 x \geq 3$

查看试题解析
5. 等腰三角形一个外角等于110°，则底角为（）

A、70°或40° B、40°或55° C、55°或70° D、70°

查看试题解析
6. 如图，等边 $△ A B C$ 的边长为 $8, A D$ 是 $B C$ 边上的中线，点 $E$ 是 $A C$ 边上的中点. 如果点 $P$ 是 $A D$ 上的动点，那么 $E P + C P$ 的最小值为（）

A、 $4$ B、 $2 \sqrt{3}$ C、 $3 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
7. 如图，函数y=kx+b（k≠0）的图象经过点B（2，0），与函数y=2x的图象交于点A ，则不等式0＜kx+b＜2x的解集为（）

A、 $1 < x < 2$ B、 $x > 2$ C、 $x > 0$ D、 $0 < x < 1$

查看试题解析
8. 下列各式中是一元一次不等式组的是（）

A、 ${\begin{array}{l} x + 3 < 2 \\ \frac{1}{x} + 2 \geq 5 \end{array}$ B、 ${\begin{array}{l} x + y > 4 \\ x - y < 6 \end{array}$ C、 ${\begin{array}{l} x + 4 \geq - 3 \\ 6 < 12 \end{array}$ D、 ${\begin{array}{l} x - 6 > - 2 \\ x + 1 < 8 \end{array}$

查看试题解析
9. 为鼓励市民节约用水，某地自来水公司推出如下收费标准：若每户每月用水不超过5立方米，则每立方米收费2元；若每户每月用水超过5立方米，则超过部分每立方米收费2.5元，已知小明家每月水费都不超过17元，则小明家每月用水量（每月用水量是正整数）至多是（）

A、6立方米 B、7立方米 C、8立方米 D、9立方米

查看试题解析
10. 如图，在△ABC中，∠B＝∠C＝60°，点D在AB边上，DE⊥AB，并与AC边交于点E．如果AD＝1，BC＝6，那么CE等于（）

A、5 B、4 C、3 D、2

查看试题解析
11. 将点 $A (3, 2)$ 向下平移 $2$ 个单位长度后，再向左平移 $4$ 个单位长度的点为（）

A、 $(- 1, 0)$ B、 $(5, 6)$ C、 $(8, - 4)$ D、 $(1, 2)$

查看试题解析
12. 如图，点P是∠BAC内一点，且点P到AB，AC的距离相等，则△PEA≌△PFA的理由是（）

A、HL B、AAS C、SSS D、ASA

查看试题解析

二、填空题（本题共计 4 小题，每题 3 分，共计12分）

13. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ C A B$ ， $B C = 8 c m$ ， $B D = 5 c m$ ，那么D点到直线 $A B$ 的距离是 $c m$ ．

查看试题解析
14. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C D$ 是斜边 $A B$ 上的中线， $E$ 、 $F$ 分别为 $D B$ 、 $B C$ 的中点，若 $A B = 8$ ，则 $E F =$ ．

查看试题解析
15. 如图，已知，OE平分∠AOB，OF平分∠BOC，∠EOF=65°，则∠AOC=度

查看试题解析
16. 关于 $x$ 的不等式组 ${\begin{array}{l} \frac{x - 2}{4} < \frac{x - 1}{3} ， \\ 3 x - 2 m \leq 2 - x \end{array}$ 有且只有4个整数解，则 $m$ 的取值范围是.

查看试题解析

三、解答题（本题共计 7 小题，每题 10 分，共计70分）

17. 某学校九年级举行乒乓球比赛，准备发放一些奖品进行奖励，奖品设为一等奖和二等奖．已知购买一个一等奖奖品比购买一个二等奖奖品多用20元．若用400元购买一等奖奖品的个数是用160元购买二等奖奖品个数的一半．

(1)、求购买一个一等奖奖品和一个二等奖奖品各需多少元？

(2)、经商谈，商店决定给予该学校购买一个一等奖奖品即赠送一个二等奖奖品的优惠，如果该学校需要二等奖奖品的个数是一等奖奖品个数的2倍还多8个，且该学校购买两个奖项奖品的总费用不超过670元，那么该学校最多可购买多少个一等奖奖品？

查看试题解析
18. 某酒店在重新装修后，准备在大厅的主楼梯上铺设某种红色地毯，已知这种地毯每平方米的售价为40元，主楼梯道宽为3米，其侧面如图所示；铺设梯子的红地毯至少需要多长？花费至少多少元？

查看试题解析
19. 解不等式或不等式组

(1)、 $5 x + 3 < 3 (2 + x)$

(2)、 ${\begin{array}{l} 5 x - 2 > 3 (x + 1) \\ \frac{1}{2} x - 1 \leq 7 - \frac{3}{2} x \end{array}$

查看试题解析
20. 已知：如图△ABC，
求作：一点P，使P在BC上，且点P到∠BAC的两边的距离相等.

(要求尺规作图，并保留作图痕迹，不要求写作法)

查看试题解析
21. 根据不等式的性质，将下列不等式化成“ $x > a$ ”或“ $x < a$ ”的形式．

(1)、 $- \frac{2}{3} x < - 2$ ．

(2)、 $10 x > 7 x + 1$ ．

查看试题解析
22. 解不等式组，并把解集在数轴上表示出来
${\begin{matrix} 3 x - 2 \leq x \\ \frac{1 + 2 x}{5} < \frac{x + 1}{2} \end{matrix}$ ．

查看试题解析
23. 若不等式3（x﹣1）≤mx²+nx﹣3是关于x的一元一次不等式，求m、n的取值．

查看试题解析

江西省九江市重点校2023-2024学年八年级下学期数学期中试题

一、选择题 （本题共计 12 小题 ，每题 3 分 ，共计36分 ）

二、填空题 （本题共计 4 小题 ，每题 3 分 ，共计12分 ）

三、解答题 （本题共计 7 小题 ，每题 10 分 ，共计70分 ）

一、选择题（本题共计 12 小题，每题 3 分，共计36分）

二、填空题（本题共计 4 小题，每题 3 分，共计12分）

三、解答题（本题共计 7 小题，每题 10 分，共计70分）