江西省九江市修水县2023-2024学年七年级下学期数学期中试题
试卷更新日期:2024-06-13 类型:期中考试
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)
-
1. 下列计算中正确的是( )A、 B、 C、 D、2. 如图,过直线外一点画已知直线的平行线的方法,其依据是( )
 A、同旁内角互补,两直线平行 B、两直线平行,同位角相等 C、同位角相等,两直线平行 D、内错角相等,两直线平行3. 下列多项式的乘法中可用平方差公式计算的是( )A、(1+x)(x+1) B、(﹣a+b)(a﹣b) C、(x2﹣y)(y2+x) D、(a+b)(b﹣a)4. 某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):
A、同旁内角互补,两直线平行 B、两直线平行,同位角相等 C、同位角相等,两直线平行 D、内错角相等,两直线平行3. 下列多项式的乘法中可用平方差公式计算的是( )A、(1+x)(x+1) B、(﹣a+b)(a﹣b) C、(x2﹣y)(y2+x) D、(a+b)(b﹣a)4. 某科研小组在网上获取了声音在空气中传播的速度与空气温度之间的关系的一些数据(如下表):温度(℃)
-20
-10
0
10
20
30
声速()
318
324
330
336
342
348
下列说法中错误的是( )
A、当空气温度为时,5s内声音可以传播 B、温度每升高 , 声速增加 C、在这个变化过程中,自变量是温度,因变量是声速 D、温度越高,声速越快5. 把一副三角尺按如图所示的方式摆放,使 . 若点 E 恰好落在的延长线上,则的大小为( ) A、 B、 C、 D、6. 兄弟两人沿五四广场的木栈道跑步,领先的哥哥看弟弟跑的慢,就停下来看风景.过了一会发现弟弟跑前面去了,急忙追赶,结果比弟弟提前到达终点.用分别表示弟弟和哥哥所跑的路程,t为跑步时间,则下列图象中与故事情节相吻合的是( )A、
A、 B、 C、 D、6. 兄弟两人沿五四广场的木栈道跑步,领先的哥哥看弟弟跑的慢,就停下来看风景.过了一会发现弟弟跑前面去了,急忙追赶,结果比弟弟提前到达终点.用分别表示弟弟和哥哥所跑的路程,t为跑步时间,则下列图象中与故事情节相吻合的是( )A、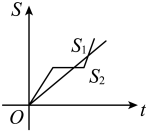 B、
B、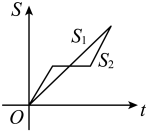 C、
C、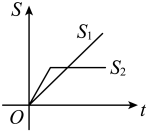 D、
D、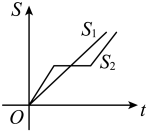
二、填空题(本大题共6小题,每小题3分,共18分)
-
7. 一种流感病毒的直径约为0.00000056米,数0.00000056用科学记数法表示为。8. 计算: .9. 如图,一束光线从点C出发,经过平面镜反射后,反射光线 , 此时 . 若测得 , 则的度数为 .
 10. 已知:2x+3y+3=0,计算:4x•8y的值= .11. 一辆汽车加满油后,油箱中有汽油55升,汽车行驶时正常的耗油量为每千米0.1升,则加满油后,油箱中剩余的汽油量y(升)关于已行驶的里程的函数解析式为 .12. 一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形 , 改变三角板的位置(其中A点位置始终不变),当时, .
10. 已知:2x+3y+3=0,计算:4x•8y的值= .11. 一辆汽车加满油后,油箱中有汽油55升,汽车行驶时正常的耗油量为每千米0.1升,则加满油后,油箱中剩余的汽油量y(升)关于已行驶的里程的函数解析式为 .12. 一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形 , 改变三角板的位置(其中A点位置始终不变),当时, .
三、(本大题共5小题,每小题6分,共30分)
-
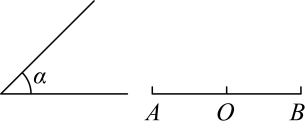
13. 计算:14. 计算:15. 如图,已知锐角和平角 , 在内部求作 , 使与互补.(不要求尺规作图)
 16. 如图,直线AB,CD,EF相交于点O.若∠COF=120°,∠AOD=100°,求∠AOF的度数.
16. 如图,直线AB,CD,EF相交于点O.若∠COF=120°,∠AOD=100°,求∠AOF的度数. 17. 假设圆柱的高是8cm,圆柱的底面半径由小到大变化时,圆柱的体积也随之发生变化.(1)、在这个变化的过程中,自变量为 , 因变量为 .(2)、如果圆柱底面半径为r(cm),那么圆柱的体积V(cm3)可以表示为 .(3)、当r由1cm变化到6cm时,V由cm3变化到cm3 .
17. 假设圆柱的高是8cm,圆柱的底面半径由小到大变化时,圆柱的体积也随之发生变化.(1)、在这个变化的过程中,自变量为 , 因变量为 .(2)、如果圆柱底面半径为r(cm),那么圆柱的体积V(cm3)可以表示为 .(3)、当r由1cm变化到6cm时,V由cm3变化到cm3 .四、(本大题共3小题,每小题8分,共24分)
-
18. 阅读材料,并解答问题.
例:用简便方法计算195×205.
解:195×205
=(200-5)×(200+5)①
=2002-52②
=39975.
(1)、例题求解过程中,第②步变形是利用(填乘法公式的名称);(2)、用简便方法计算:9×11×101.19. 如图,已知 , . (1)、与平行吗?请说明理由.(2)、与的位置关系如何?为什么?20. 小华同学在保养自己的山地自行车时发现,自行车每节链条的长度为 , 重叠部分的圆的直径为 .
(1)、与平行吗?请说明理由.(2)、与的位置关系如何?为什么?20. 小华同学在保养自己的山地自行车时发现,自行车每节链条的长度为 , 重叠部分的圆的直径为 . (1)、观察图形填表:
(1)、观察图形填表:链条节数/节
2
3
4
链条长度/
(2)、如果x节链条的总长度是 , 求y与x之间的关系式.五、(本大题共2小题,每小题9分,共18分)
-
21. 探究应用:(1)、计算:=;= .(2)、上面的乘法计算结果很简洁,你发现了什么规律(公式)?
用含的字母表示该公式为: .
(3)、下列各式能用第(2)题的公式计算的是( ).A、 B、 C、 D、22. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离与甲车行驶的时间之间的关系如图所示. (1)、A , B两城相距 .(2)、乙车比甲车晚出发h , (填“甲车”或“乙车”)先到达B城.(3)、乙车出发多少小时后追上甲车?(4)、当甲、乙两车相距时,甲车行驶的时间是多少?(请求出所有情况)
(1)、A , B两城相距 .(2)、乙车比甲车晚出发h , (填“甲车”或“乙车”)先到达B城.(3)、乙车出发多少小时后追上甲车?(4)、当甲、乙两车相距时,甲车行驶的时间是多少?(请求出所有情况)六、(本大题共12分)
-
23. 综合与探究
数学活动课上,老师以“一个含的直角三角板和两条平行线”为背景展开探究活动,

如图1,已知直线 , 直角三角板中, , .
(1)、如图1,若 , 则;(直接写出答案)(2)、“启航”小组在图1的基础上继续展开探究:如图 , 调整三角板的位置,当三角板的直角顶点在直线上,直线与 , 相交时,他们得出的结论是: , 你认为启航小组的结论是否正确,请说明理由;(3)、如图 , 受到“启航”小组的启发,“睿智”小组提出的问题是:在图的基础上,继续调整三角板的位置,当点不在直线上,直线与 , 相交时,与有怎样的数量关系?请你用平行线的知识说明理由.