云南省楚雄彝族自治州2023-2024学年八年级下学期4月期中数学试题
试卷更新日期:2024-06-13 类型:期中考试
一、选择题(本大题共15小题,每小题只有一个正确选项,每小题2分,共30分)
-
1. 化简:=( )A、-2 B、2 C、4 D、-42. 的倒数是( )A、 B、- C、 D、-3. 如果二次根式有意义,那么x的取值范围是( )A、x≥-1 B、x>-1 C、x≤-1 D、x<14. 四边形ABCD中,AD∥BC.要判别四边形ABCD是平行四边形,还需满足条件( )A、∠A+∠C=180° B、∠B+∠D=180° C、∠B+∠A=180° D、∠A+∠D=180°5. 下列根式中是最简二次根式的是( )A、 B、 C、 D、6. 下列各组数中,以a , b , c为边的三角形是直角三角形的是( )A、a=3,b=5,c=4 B、a=3,b=3,c=5 C、a=4,b=4,c=4 D、a=5,b=5,c=37. 菱形具有而矩形不一定具有的性质是 ( )
A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角互补8. 下列运算中,正确的是( )A、 B、 C、 D、9. 下列命题中正确的是( )A、对角线互相平分的四边形是菱形 B、对角线互相平分且相等的四边形是菱形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分的四边形是菱形10. 如果正方形的对角线长是 , 则它的边长是( )A、2 B、 C、2 D、111. 正方形、菱形、矩形都具有的性质是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分一组对角12. 如图,已知△ABC中,AB=6,BC=8,AC=10,那么AC边上的中线BD的长为( ) A、3 B、4 C、5 D、613. 如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1 , S2 , S3 , 且S1=4,S2=12,
A、3 B、4 C、5 D、613. 如图所示,以Rt△ABC的三边向外作正方形,其面积分别为S1 , S2 , S3 , 且S1=4,S2=12,则S3=( )
 A、4 B、12 C、16 D、6414. 已知= , 则=( )A、3 B、5 C、 D、15. 已知菱形的周长是20,其中一条对角线的长是8,则另一条对角线的长是( )A、5 B、6 C、8 D、10
A、4 B、12 C、16 D、6414. 已知= , 则=( )A、3 B、5 C、 D、15. 已知菱形的周长是20,其中一条对角线的长是8,则另一条对角线的长是( )A、5 B、6 C、8 D、10二、填空题(本大题共4小题,每小题2分,共8分)
-
16. 9的相反数是.17. 菱形的两条对角线分别是6cm,8cm,则菱形的面积为cm2 .18. 如图,A、B两点被池塘隔开,A、B、C三点不共线.设AC、BC的中点分别为M、N . 若MN=3米,则AB=米.
 19. 如图,D为△ABC的边BC上一点,已知 AB=13,AD=12,AC=15,BD=5,则DC的长为 .
19. 如图,D为△ABC的边BC上一点,已知 AB=13,AD=12,AC=15,BD=5,则DC的长为 .
三、解答题(本大共8小题,共62分)
-
20. 计算:21. 计算:22. 如图,已知E,F是平行四边形ABCD的对角线AC上的两点,BE∥DF,求证:CE=AF.
 23. 如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在ED的位置上,测得BD长为0.5米,求梯子顶端A下落了多少米?
23. 如图,一个梯子AB长2.5米,顶端A靠在墙AC上,这时梯子下端B与墙角C距离为1.5米,梯子滑动后停在ED的位置上,测得BD长为0.5米,求梯子顶端A下落了多少米? 24. 如图所示,在矩形ABCD中,AB=8,AD=10,将矩形沿直线AE折叠,顶点D恰好落在BC边上的点F处,求CE的长.
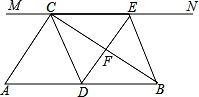
24. 如图所示,在矩形ABCD中,AB=8,AD=10,将矩形沿直线AE折叠,顶点D恰好落在BC边上的点F处,求CE的长. 25. 如图,在△ABC中,AB=BC,BD平分∠ABC.四边形ABED是平行四边形,DE交BC于点F,连接CE.
25. 如图,在△ABC中,AB=BC,BD平分∠ABC.四边形ABED是平行四边形,DE交BC于点F,连接CE.求证:四边形BECD是矩形.