安徽省合肥市庐江县2023-2024学年七年级下学期数学期中试题

试卷更新日期：2024-06-13 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题4分，满分40分）每小题都给出A、B、C、D四个选项，其中只有一个是正确的．

1. 下面实数中，是无理数的是（）

A、 $\sqrt{2}$ B、 $\sqrt{4}$ C、3.1415 D、 $\frac{23}{7}$

查看试题解析
2. 在平面直角坐标系中，点 $P (0, - 2)$ 在（）

A、 $x$ 轴上 B、 $y$ 轴上 C、第二象限 D、第四象限

查看试题解析
3. 过点 $P$ 作 $A B$ 的垂线 $C D$ ，下列选项中，三角板的放法正确的是（）

A、 B、 C、 D、

查看试题解析
4. 下列说法正确的是（）

A、1的算术平方根是 $\pm 1$ B、 $- 4$ 没有立方根 C、 $\frac{1}{16}$ 的平方根是 $\frac{1}{4}$ D、 $- 5$ 的立方根是 $\sqrt[3]{- 5}$

查看试题解析
5. 如图，直线a∥b，直角三角板ABC的直角顶点C在直线b上，若∠1＝55°，则∠2＝（）

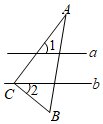A、55° B、45° C、35° D、25°

查看试题解析
6. 下列各数中，与 $2 - \sqrt{3}$ 的和为有理数的是（）

A、 $2 \sqrt{3}$ B、 $5 + \sqrt{3}$ C、 $\sqrt{2}$ D、 $5 - \sqrt{3}$

查看试题解析
7. 下列六个命题：①对顶角相等；②内错角相等；③平行于同一条直线的两条直线互相平行；④带根号的数一定是无理数；⑤每个有理数都可以用数轴上唯一的点来表示；⑥数轴上每一个点都表示唯一一个实数；其中真命题的的个数有（）

A、1 B、2 C、3 D、4

查看试题解析
8. 在平面直角坐标系中， $A B ∥ x$ 轴， $A B = 2$ ，若点 $A (1 ， - 3)$ ，则点B的坐标是（）

A、 $(1 ， - 1)$ B、 $(1 ， - 5)$ 或 $(1 ， - 1)$ C、 $(3 ， - 3)$ D、 $(- 1 ， - 3)$ 或 $(3 ， - 3)$

查看试题解析
9. 如图，下列判断中错误的是（）

A、 $∵ A B ∥ C D$ ， $∴ ∠ B A C = ∠ A C D$ B、 $∵ ∠ B A D + ∠ A D C = 180 °$ ， $∴ A B ∥ C D$ C、 $∵ A D ∥ B C$ ， $∴ ∠ B C A = ∠ D A C$ D、 $∵ ∠ A B D = ∠ C D B$ ， $∴ A D ∥ B C$

查看试题解析
10. 如图，锐角三角形 $A B C$ 中， $∠ B A C = 45 °$ ，将三角形 $A B C$ 沿着射线 $B C$ 方向平移得到三角形 $A^{'} B^{'} C^{'}$ （平移后点 $A$ ， $B$ ， $C$ 的对应点分别是点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ ），连接 $C A^{'}$ ，若在整个平移过程中， $∠ A C A^{'}$ 和 $∠ C A^{'} B^{'}$ 的度数之间存在2倍关系，则 $∠ A C A^{'}$ 不可能的值为（）

A、 $15 °$ B、 $30 °$ C、 $45 °$ D、 $90 °$

查看试题解析

二、填空题（本大题共4题，每小题5分，满分20分）

11. 如图，直线 $a$ 与直线 $b$ 相交于点 $O$ ， $∠ 1 = 30 °$ ， $∠ 2 =$ ．

查看试题解析
12. 如图，已知A村庄的坐标为 $(2 ， - 3)$ ，一辆汽车从原点O出发在x轴上行驶.行驶过程中汽车离A村最近的距离为.

查看试题解析
13. 如图，面积为2的正方形 $A B C D$ 的顶点 $A$ 在数轴上，且表示的数为 $- 1$ ，若 $A E = A B$ ，则数轴上的点 $E$ 所表示的数为．

查看试题解析
14. 如图， $P Q ∥ M N$ ， $l ⊥ M N$ ，垂足为A ， $l$ 交 $P Q$ 于点 $B$ ，点 $C$ 在射线 $A M$ 上．
①若 $B C$ 平分 $∠ P B A$ ，则 $∠ B C M =$ ．
②若 $∠ A C B < 60 °$ ，在直线 $P Q$ 上取一点 $D$ ，连接 $C D$ ，过点 $D$ 作 $D E ⊥ C D$ ，交直线 $l$ 于点 $E$ ，若 $∠ B D E = 30 °$ ，则 $∠ A C D =$ ．

查看试题解析

三、（本大题共2小题，每小题8分，满分16分）

15. 计算： $- 2^{2} + \sqrt{49} + \sqrt[3]{- 27}$ ．

查看试题解析
16. 如图，在平面直角坐标系 $x O y$ 中，三角形 $A B C$ 的三个顶点坐标分别为 $A (2, 0)$ ， $B (2, 6)$ ， $C (- 1, 2)$ ，点 $A^{'}$ 的坐标是 $(- 2, - 1)$ ，现将三角形 $A B C$ 平移，使点 $A$ 平移到点 $A^{'}$ 处， $B^{'}$ ， $C^{'}$ 分别是 $B$ ， $C$ 的对应点．

(1)、画出平移后的三角形 $A^{'} B^{'} C^{'}$ （不写画法）；

(2)、若将 $C$ 点向右平移 $m (m > 0)$ 个单位长度到点 $D$ ，使得三角形 $A B D$ 的面积等于3，求 $m$ 的值．

查看试题解析

四、（本大题共2小题，每小题8分，满分16分）

17. 已知实数 $a + 9$ 的一个平方根是 $- 5$ ， $2 b - a$ 的立方根是 $- 2$ ，求 $2 a + b$ 的算术平方根.

查看试题解析
18. 完成下面的证明．
如图，在 $△ A B C$ 中， $B D$ 平分 $∠ A B C$ ， $C E$ 平分 $∠ A C B$ ， $∠ A B C = ∠ A C B$ ， $C E ∥ D F$ ．
求证： $∠ D B F = ∠ F$ ．
证明： $∵ B D$ 平分 $∠ A B C$ ， $C E$ 平分 $∠ A C B$ （已知），
$∴ ∠ D B C = \frac{1}{2} ∠ A B C$ ， $∠ E C B = \frac{1}{2} ∠ A C B$ （    ）．
又 $∵ ∠ A B C = ∠ A C B$ （已知），
$∴ ∠ D B C = ∠$     ▲    （等量代换）．
又 $C E ∥ D F$ （已知），
$∴ ∠ E C B = ∠$     ▲     ，（    ）．
$∴ ∠ D B F = ∠ F$ ．（等量代换）．

查看试题解析

五、（本大题共2小题，每小题10分，满分20分）

19. 如图，在平面直角坐标系中， $O A_{1} = O A_{2} = A_{1} A_{2} = A_{2} A_{4} = A_{4} A_{5} = A_{4} A_{6} = A_{5} A_{6} = A_{6} A_{8} = ⋯ = 2$ ， $A_{2} A_{3} = A_{3} A_{4} = A_{6} A_{7} = A_{7} A_{8} = A_{10} A_{11} = A_{11} A_{12} = ⋯ = \sqrt{2}$ ．

(1)、① $A_{19}$ 的坐标为；② $A_{2024}$ 的坐标为．

(2)、 $n$ 是正整数，用含 $n$ 的代数式表示 $A_{4 n + 3}$ 坐标； $A_{4 n + 3}$ 的坐标为．

(3)、点 $P$ 从点 $O$ 出发，沿着点 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， $⋯$ 运动，到点 $A_{200}$ 时运动停止，求点 $P$ 运动的路程．

查看试题解析
20. 如图， $∠ A O B = 40 °$ ， $O C$ 平分 $∠ A O B$ ，点 $E$ 在射线 $O C$ 上， $E D ⊥ O A$ ，垂足为点 $D$ ， $D F$ 平分 $∠ O D E$ ，交射线 $O C$ 于点 $F$ ，动点 $P$ 从点 $O$ 出发沿射线 $O C$ 运动，连接 $D P$ ．

(1)、当 $D P$ 平分 $∠ O D F$ 时， $∠ P D E =$ $°$ ；

(2)、当 $D P ∥ O B$ 时，求 $∠ P D E$ 的度数；

(3)、当 $D P ⊥ F D$ 时，求 $∠ A D P$ 的度数．

查看试题解析

六、（本题满分12分）

21. 如图1，已知，点 $A (1, 4)$ ， $A H ⊥ x$ 轴，垂足为 $H$ ，将线段 $A O$ 平移至线段 $B C$ ，点 $B (3, 0)$ ，其中点 $A$ 与点 $B$ 对应，点 $O$ 与点 $C$ 对应．

(1)、三角形 $A O H$ 的面积为．

(2)、如图1，若点 $D (m, n)$ 在线段 $O A$ 上，请你连接 $D H$ ，利用图形面积关系说明 $n = 4 m$ ．

(3)、如图2，连 $O C$ ，动点 $P$ 从点 $B$ 开始在 $x$ 轴上以每秒2个单位的速度向左运动，同时点 $Q$ 从点 $O$ 开始在 $y$ 轴上以每秒1个单位的速度向下运动．若经过 $t$ 秒，三角形 $A O P$ 与三角形 $C O Q$ 的面积相等，试求 $t$ 的值及点 $P$ 的坐标．

查看试题解析

七、（本题满分12分）

22. 对于实数a，我们规定：用符号 $[\sqrt{a}]$ 表示不大于 $\sqrt{a}$ 的最大整数，称 $[\sqrt{a}]$ 为a的根整数，例如： $[\sqrt{9}] = 3$ ， $[\sqrt{10}]$ =3．

(1)、仿照以上方法计算： $[\sqrt{4}]$ =； $[\sqrt{26}]$ = ．

(2)、若 $[\sqrt{x}] = 1$ ，写出满足题意的x的整数值．

(3)、如果我们对a连续求根整数，直到结果为1为止．例如：对10连续求根整数2次 $[\sqrt{10}] = 3$ $\to$ $[\sqrt{3}]$ =1，这时候结果为1．
对100连续求根整数，多少次之后结果为1，请写出你的求解过程．

(4)、只需进行3次连续求根整数运算后结果为1的所有正整数中，最大的是．

查看试题解析

八、（本题满分14分）

23. 如图，直线 $P Q ∥ M N$ ，点 $C$ 是 $P Q$ ， $M N$ 之间的一个动点．

(1)、如图1，求证 $∠ D C E = ∠ 1 + ∠ 2$ ；

(2)、小明把一块三角板 $(∠ A = 30 ° ， ∠ C = 90 °)$ 如图2放置，点 $D$ ， $E$ 是三角板的边与平行线的交点．
①若 $∠ A E N = ∠ A$ ，求 $∠ B D Q$ 的度数；
②如图3，点 $G$ 在线段 $C D$ 上，连接 $E G$ ，当 $∠ C E G = ∠ C E M$ ，求 $\frac{∠ G E N}{∠ B D Q}$ 的值．

查看试题解析