湖南省常德市澧县2023-2024学年八年级下学期期中数学试题
试卷更新日期：2024-06-13 类型：期中考试
一、选择题（本大题共10个小题，每小题只有一个选项符合题意，每小题3分，共30分）
-
1. 中国“二十四节气”已被正式列入联合国教科文组织人类非物质文化遗产代表作品录，下列四幅作品分别代表“立春”、“谷雨”、“白露”、“大雪”，其中是中心对称图形的是（ ）A、
B、
C、
D、
2. 一个直角三角形的两直角边长分别为5和12，则斜边长为（ ）A、13 B、14 C、 D、153. 若一个多边形的内角和是外角和的3倍，则该多边形的边数为（ ）A、5 B、6 C、7 D、84. 如图，在中，是斜边上的中线， ， 则的度数是（ ）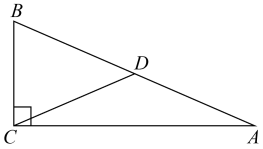
A、40° B、50° C、60° D、70°5. 如图所示，在▱ABCD中，E，F分别在BC，AD上，若想使四边形AFCE为平行四边形，须添加一个条件，这个条件可以是（ ）
①AF=CF；②AE=CF；③∠BAE=∠FCD；④∠BEA=∠FCE．
A、①或② B、②或③ C、③或④ D、①或③或④6. 如图，△ABC中，∠ACB=90°，CD是高，∠A=30°，则BD与AB的关系（ ）
A、BD=AB B、BD=AB C、BD=AB D、BD=AB7. 已知点M（3，﹣2），N（3，﹣1），则线段MN与x轴（ ）A、垂直 B、平行 C、相交 D、不垂直8. 直角三角形两锐角的平分线所夹的钝角的度数为（ ）A、100度 B、120度 C、135度 D、140度9. 如图，平地上A、B两点被池塘隔开，测量员在岸边选一点C ， 并分别找到和
中点D、E ， 测量得米，则A、B两点间的距离为（ ）
A、30米 B、32米 C、36米 D、48米10. 如图，当秋千静止时，踏板离地的垂直高度 ， 将它往前推至处时（即水平距离 ， ），踏板离地的垂直高度 ， 它的绳索始终拉直，则绳索的长是（ ）
A、 B、 C、 D、二、填空题（共8小题，每小题3分，满分24分）
-
11. 如图， 中， 于D，要使 ，若根据“ ”判定，还需要加条件
12.如图，在矩形ABCD中，BC=20cm，点P和点Q分别从点B和点D出发，按逆时针方向沿矩形ABCD的边运动，点P和点Q的速度分别为3cm/s和2cm/s，则最快 s后，四边形ABPQ成为矩形．
13.如图，将两条宽度都为3的纸条重叠在一起，使∠ABC=60°，则四边形ABCD的面积为 ．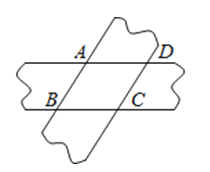
14. 如图，矩形ABCD中，AC，BD交于点O，M，N分别为BC，OC的中点，若MN=3，则BD=.
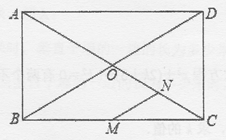15. 如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝6，BC＝9，CD＝4，则四边形ABCD的面积是.
16. 中国象棋是中华民族的文化瑰宝，它历史久远、博大精深，如图①，“马”走一步可到达A、B、C、D、E、F、G、H中的某一个位置，俗称“马走日”．在如图②所示的象棋盘中，“马”至少走步才能到达“帅”的位置．
17. 2002年国际数学家大会在中国北京举行，这是21世纪全世界数学家的第一次大聚会．这次大会的会徽就是下图，选定的是我国古代数学家赵爽用来证明勾股定理的弦图，可以说是充分肯定了我国数学的成就，也弘扬了我国古代的数学文化．弦图是由四个全等的直角三角形和中间的小正方形拼成的一个大正方形．如果大正方形的面积是13，小正方形的面积是1，直角三角形的较短直角边长为a ， 较长直角边长为b ， 那么的值是 ．
18. 如图是用边长相等的正三角形和正边形两种地砖铺设的部分地面示意图，则 ．
三、解答题（共6小题，满分46分）
-
19. 已知点 ．(1)、若点Q的坐标为 ， 直线轴，求点P的坐标；(2)、若点P在第二象限，且它到x轴、y轴的距离相等，求的值．20. 如图， ，M是中点，平分 ， 求证：平分 ．
21. 已知：如图，平行四边形ABCD中，M、N分别为AB和CD的中点.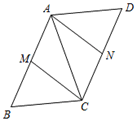
(1)、求证：四边形AMCN是平行四边形；(2)、若AC＝BC＝5，AB＝6，求四边形AMCN的面积.22. 看着冉冉升起的五星红旗，你们是否想过旗杆到底有多高呢？某数学兴趣小组为了测量旗杆高度，进行以下操作：如图1，先将升旗的绳子拉到旗杆底端，发现绳子末端刚好接触到地面；如图2，再将绳子末端拉到距离旗杆8m处，发现绳子末端距离地面2m．请根据以上测量情况，计算旗杆的高度．
