2023-2024学年人教版八年级下册期末数学全真模拟试卷(一)

试卷更新日期：2024-06-11 类型：期末考试

进入出卷网下载

一、选择题(本大题共10小题，每小题3分，满分30分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. 化简 ${(\sqrt{3} - 2)}^{2023} {(\sqrt{3} + 2)}^{2024}$ 的结果为（　　）

A、 $- 1$ B、 $\sqrt{3} - 2$ C、 $\sqrt{3} + 2$ D、 $- \sqrt{3} - 2$

查看试题解析
2. 如图，菱形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点O，若 $A C = 16$ ， $B D = 8$ ，则菱形 $A B C D$ 的边长为（）

A、 $4 \sqrt{5}$ B、 $8 \sqrt{5}$ C、8 D、10

查看试题解析
3.
如图所示，一场暴雨过后，垂直于地面的一棵树在距地面1米处折断，树尖B 恰好碰到地面，经测量AB=2米，则树高为（）

A、 $\sqrt{5}$ 米 B、 $\sqrt{3}$ 米 C、( $(\sqrt{5} + 1)$ 米 D、3 米

查看试题解析
4. 下列计算正确的是（）

A、 $3 \sqrt{2} \cdot 4 \sqrt{2} = 12 \sqrt{2}$ B、 $\sqrt{(- 9) \times (- 4)} = \sqrt{- 9} \times \sqrt{- 4} = 6$ C、 $- 3 \sqrt{\frac{2}{3}} = \sqrt{{(- 3)}^{2} \times \frac{2}{3}} = \sqrt{6}$ D、 $\sqrt{13^{2} - 12^{2}} = \sqrt{(13 + 12) (13 - 12)} = 5$

查看试题解析
5. 如图，正方形 $A B C O$ 和正方形 $D E F O$ 的顶点 $A$ ， $O$ ， $E$ 在同一直线 $l$ 上，且 $E F = \sqrt{2}$ ， $A B = 3$ ，给出下列结论：① $∠ C O D = 45 °$ ；② $A E = 6$ ；③ $C F = B D = \sqrt{17}$ ；④ $△ C O F$ 的面积是 $\frac{3}{2}$ .其中正确的结论为（）

A、①③ B、①④ C、②③ D、①③④

查看试题解析
6. 如图，DE是△ABC的中位线，若BC=8，则DE的长是（）

A、3 B、4 C、5 D、6

查看试题解析
7. 如图，点A是直线l外一点，在l上取两点B、C ，分别以A、C为圆心，BC、AB长为半径画弧，两弧交于点D ，连结AB、AD、CD，则四边形ABCD是平行四边形．其依据是（）

A、两组对边分别相等的四边形是平行四边形 B、一组对边平行且相等的四边形是平行四边形 C、两组对边分别平行的四边形是平行四边形 D、一组对边平行，另一组对边相等的四边形是平行四边形

查看试题解析
8. 如图，E，F分别是平行四边形ABCD的边AB，CD上的点，AF与DE相交于点P，BF与CE相交于点Q，若 S_△APD=a，S_△BQC=b，S_▱ABCD=c，则阴影部分的面积为（　　）

A、 $a + b$ B、 $\frac{1}{2} c - a - b$ C、 $c - 2 a - b$ D、 $2 a + b$

查看试题解析
9. 如图．在△ABC中，∠ACB＝60°，AC＝1，D是边AB的中点，E是边BC上一点．若DE平分△ABC的周长，则DE的长为（　　）

A、1 B、 $\frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{5}{3}$

查看试题解析
10. 如图，函数 $y = 2 x$ 和 $y = a x + 5$ 的图象交于点A，则不等式 $2 x < a x + 5$ 的解集是（）

A、 $x < \frac{3}{2}$ B、 $x < 3$ C、 $x > \frac{3}{2}$ D、 $x > 3$

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分.）

11. 要使二次根式 $\sqrt{x - 2}$ 有意义，则x的值可以是（写出一个即可）

查看试题解析
12. 等腰梯形的上底是10cm，下底是16cm，高是4cm，则等腰梯形的周长为cm．

查看试题解析
13. 如图，在矩形ABCD中，AC、BD交于点O，DE⊥AC于点E，若∠AOD=110°，则∠CDE=°。

查看试题解析
14. 如图，△ABC的三边长为5，12，13，分别以三边为直径向上作三个半圆．则阴影部分的面积为．

查看试题解析
15. 图1是由两个全等直角三角形和两个长方形组成的□ABCD ，将其剪拼成不重叠，无缝隙的大正方形（如图2）.记①，②，③，④的面积分别为S₁ ， S₂ ， S₃ ， S₄ ，已知S₃=4S₂.

(1)、 $S_{1}^{} : S_{2}^{}$ =；

(2)、若□ABCD的周长比长方形③的周长大18，则BC为．

查看试题解析

三、解答题(本大题共8小题，满分72分.解答应写出文字说明、证明过程或演算步骤.)

16. 计算.

(1)、 $\sqrt{8} + 3 \sqrt{2} - \sqrt{18}$

(2)、 $\sqrt{12} + | \sqrt{3} - 2 | + {(\frac{1}{2})}^{- 1}$

查看试题解析
17. 如图，正方形网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．在图中以格点为顶点画一个三角形，使三角形的其中两边的边长为 $\sqrt{5}$ 和 $\sqrt{13}$ ．

查看试题解析
18. 如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使得CF=BE，连接DF，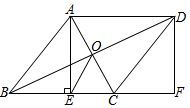

(1)、求证：四边形AEFD是矩形；

(2)、连接OE，若AB＝13，OE＝2 $\sqrt{13}$ ，求AE的长．

查看试题解析
19. 在进行化简二次根式 $\frac{1}{\sqrt{2} + 1}$ 时，通常有如下两种方法：
方法一： $\frac{1}{\sqrt{2} + 1} = \frac{1 \times (\sqrt{2} - 1)}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{2 - 1} = \sqrt{2} - 1$ ；
方法二： $\frac{1}{\sqrt{2} + 1} = \frac{2 - 1}{\sqrt{2} + 1} = \frac{{(\sqrt{2})}^{2} - 1}{\sqrt{2} + 1} = \frac{(\sqrt{2} + 1) (\sqrt{2} - 1)}{\sqrt{2} + 1} = \sqrt{2} - 1$ ；

(1)、请用以上两种方法化简： $\frac{2}{\sqrt{3} + 1}$ ；

(2)、计算： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + ⋯ + \frac{1}{\sqrt{2023} + \sqrt{2021}}$ ；

(3)、若 $a = \frac{1}{\sqrt{2} + 1}$ ，求 $3 a^{2} + 6 a + 5$ 的值.

查看试题解析
20. 如图，一张长方形纸片ABCD ，长 $B C = 20 c m$ ，宽 $A B = 16 c m$ ；将纸片沿着直线AE折叠，点D恰好落在BC边上的点F处，解答下列问题：

(1)、求BF的长；

(2)、求EC的长．

查看试题解析
21. 如图，在平行四边形ABCD中， $A B = 10 c m$ ， $A D = 20 c m$ ，平行四边形ABCD的面积为 $160 c m^{2}$ ．点P从点A出发，以1cm/s的速度沿线段AD向点D运动；同时点Q从点C出发，以3cm/s的速度沿CB向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设P、Q运动时间为t秒，回答下列问题：

(1)、求t为何值时，四边形PDCQ是平行四边形？此时平行四边形PDCQ是否是菱形？请说明理由．

(2)、是否存在t的值，使得 $△ D Q C$ 是等腰三角形？若存在，请求出t的值；若不存在，请说明理由．

查看试题解析
22. 综合运用：

(1)、【模型建立】如图1，等腰 $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $C B = C A$ ，直线 $E D$ 经过点C ，过点A作 $A D ⊥ E D$ 于点D ，过点B作 $B E ⊥ E D$ 于点E ，求证： $△ B E C ≌ △ C D A$ ．

(2)、【模型应用】如图2，已知直线 $l_{1} : y = 2 x + 4$ 与x轴交于点A ，与y轴交于点B ，将直线 $l_{1}$ 绕点A逆时针旋转 $45 °$ 至直线 $l_{2}$ ，求直线 $l_{2}$ 的函数表达式；

查看试题解析
23. 综合与实践探究
【问题背景】学习三角形旋转之后，八1班各学习小组打算用两个大小不同的等腰直角三角形通过、旋转变换设计本组的logo，小鸣在设计logo的过程中发现两个三角形在旋转过程中，某些边和角存在一定的关系。因此他和同学一起对这个问题进行了数学探究。
已知 $△ A B C$ 和 $△ A D E$ 都是等腰直角三角形，且 $∠ B A C = ∠ D A E = 90 °$

(1)、【初步探究】小鸣将 $△ A D E$ 绕点A在平面内自由旋转，连接BD、CE后，他发现这两条线段存在着一定的数量关系，如图1，请探究线段BD、CE的数量关系，并说明理由。

(2)、【深入探究】若 $∠ A D B = 90 °$ ，在旋转过程中，当点D、点E和BC的中点O三点共线时，如图2，请探究线段BD、DO和OE的数量关系，并说明理由。

(3)、【应用探究】如图2，在（2）的条件下，若 $∠ B A D = 30 °$ ， $A B = 4$ ，则 $O D =$ （直接写出结果）

(4)、【拓展探究】如图3， $∠ B D C = 60 °$ ， $B D = 2 \sqrt{3}$ ， $A D = \sqrt{42}$ ，则 $C D =$ （直接写出结果）

查看试题解析