2023-2024学年人教版七年级下册期末数学全真模拟试卷(二)

试卷更新日期：2024-06-11 类型：期末考试

进入出卷网下载

一、选择题(本大题共10小题，每小题3分，满分30分.在每小题给出的四个选项中，只有一项是符合题目要求的. )

1. 如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标，其中可以看成是由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. 若点 $A (- 5 ， y)$ 在第二象限，则点 $B (- 5 ， - y)$ 在（）．

A、第四象限 B、第三象限 C、第二象限 D、第一象限

查看试题解析
3. 下列各组数中，是二元一次方程 $5 x - y = 4$ 的一个解的是（）

A、 $\{\begin{cases} x = 1 \\ y = 3 \end{cases}$ B、 $\{\begin{cases} x = 3 \\ y = 1 \end{cases}$ C、 $\{\begin{cases} x = 0 \\ y = 4 \end{cases}$ D、 $\{\begin{cases} x = 2 \\ y = 6 \end{cases}$

查看试题解析
4. 估算 $\sqrt{26}$ 的值( )

A、在6与7之间 B、在5与6之间 C、在4与5之间 D、在3与4之间

查看试题解析
5. 如图，若∠1=∠2，DE∥BC，则：①FG∥DC；②∠AED=∠ACB；③CD平分∠ACB；④∠1+∠B=90°；⑤∠BFG=∠BDC，⑥∠FGC=∠DEC+∠DCE，其中正确的结论是（）

A、①②③ B、①②⑤⑥ C、①③④⑥ D、③④⑥

查看试题解析
6. 下列命题中，假命题是( )

A、同一平面内，过一点有且只有一条直线与已知直线垂直 B、对顶角相等 C、如果 $a / / b, c / / b$ ，那么 $a / / c$ D、过一点有且只有一条直线与已知直线平行

查看试题解析
7. 若P为直线l外一定点，A为直线l上一点，且 $P A = 3$ ， d为点P到直线l的距离，则d的取值范围为（　　）

A、 $0 < d < 3$ B、 $0 \leq d < 3$ C、 $0 < d \leq 3$ D、 $0 \leq d \leq 3$

查看试题解析
8. 某班数学兴趣小组对不等式组 ${\begin{array}{l} x > 3 \\ x \leq a \end{array}$ ，讨论得到以下结论：
①若 $a = 5$ ，则不等式组的解集为 $3 < x \leq 5$ ；
②若 $a = 2$ ，则不等式组无解；
③若不等式组无解，则a的取值范围为 $a < 3$ ；
④若不等式组只有两个整数解，则a的取值范围是 $5 \leq x < 6$ ．
其中，正确的结论的序号是（）

A、①② B、①②③ C、①②④ D、①②③④

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分.）

9. 已知关于x、y的方程组 ${\begin{array}{l} 3 x + 2 y = a + 2 \\ 2 x + 3 y = 3 - a \end{array}$ ，则x+y的值为．

查看试题解析
10. 如果实数 $x 、 y$ 满足方程组 ${\begin{array}{l} x - 2 y = 2024 \\ x + 4 y = 2022 \end{array}$ ，则 $x + y =$ ．

查看试题解析
11. 在实数 $\sqrt{2}$ ， $- 1$ ， 0， $\sqrt{5}$ ， $π$ 中，最大的无理数是．

查看试题解析
12. 已知如图， $A D ∥ B C$ ， $B D ∥ A E$ ， DE平分 $∠ A D B$ ，且 $E D ⊥ C D$ ，若 $∠ A E D + ∠ B A D = 128 °$ ，则 $∠ B C D - ∠ E A B =$ 度．

查看试题解析

三、解答题(本大题共8小题，满分72分.解答应写出文字说明、证明过程或演算步骤.)

13.

(1)、计算： $\sqrt{25} - \sqrt[3]{- 8} - (\sqrt{2})^{2} - | - \sqrt{2} |$ ；

(2)、解方程组： ${\begin{array}{l} x + 2 y = 6 \\ 2 (x + 1) - y = 4 \end{array}$ ．

查看试题解析
14. 如图，数轴的正半轴上有A，B，C三点，表示1和 $\sqrt{2}$ 的对应点分别为A，B，点B到点A的距离与点C到原点的距离相等，设点C所表示的数为 $x$ ．
(1)       请你直接写出 $x$ 的值；
(2)       求 ${(x - \sqrt{2})}^{2}$ 的平方根.


查看试题解析
15. 某校组织开展了丰富多彩的主题活动，设置了“A．诗歌朗诵表演； B．歌舞表演； C．书画作品展览； D．手工作品展览” 四个专项，每个学生只能报名参加其中一个专项．为了解活动开展情况，学校随机抽取了部分学生进行调查，绘制了如图所示的不完整的条形统计图和扇形统计图．

(1)、本次随机调查的学生人数是人．

(2)、请你补全条形统计图．

(3)、在扇形统计图中， “B”所在扇形的圆心角为 °

(4)、若该校有学生 1800 人，则全校选择“D．手工作品展览”的学生约有多少人？

查看试题解析
16. 如图，直线AB，CD分别与直线AC相交于点A，C，与直线BD相交于点B，D.若∠1＝∠2，∠3＝75°，求∠4的度数.

查看试题解析
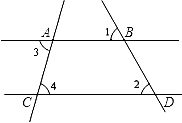17. 若关于x的方程 $3 (x + 4) = 2 a + 5$ 的解大于关于x的方程 $\frac{(4 a + 1) x}{4} = \frac{a (3 x - 4)}{3}$ 的解，求a的取值范围.

查看试题解析

18.

2022

年冬奥会上智慧化全覆盖，机器人得到广泛应用，冬奥会组委会针对不同的物品运送场景选取了几个不同类型的智能物流机器人

.

这样不仅能高效运输，同时也能减少人员接触。具体运输情况如表所示：

	$A$ 型机器人 $/$ 个	$B$ 型机器人 $/$ 个	运输物品总数 $/$ 件
第一批	$2$	$5$	$34$
第二批	$4$	$3$	$26$

问：

(1)、每个

A

型机器人和

B

型机器人分别可以运输物品多少件？

(2)、若每个

A

型机器人售价

3

万元，每个

B

型机器人售价

2.5

万元，该公司计划采购

A

，

B

两种型号的机器人共

20

个，总费用不超过

55

万元，那么

A

型号机器人最多购买多少个？

查看试题解析

19. 问题情境：
在平面直角坐标系xOy中有不重合的两点A（x₁ ， y₁）和点B（x₂ ， y₂），小明在学习中发现，若x₁=x₂ ，则AB∥y轴，且线段AB的长度为|y₁﹣y₂|；若y₁=y₂ ，则AB∥x轴，且线段AB的长度为|x₁﹣x₂|；

（应用）：

(1)、若点A（﹣1，1）、B（2，1），则AB∥x轴，AB的长度为．

(2)、若点C（1，0），且CD∥y轴，且CD=2，则点D的坐标为．

(3)、（拓展）：
我们规定：平面直角坐标系中任意不重合的两点M（x₁ ， y₁），N（x₂ ， y₂）之间的折线距离为d（M，N）=|x₁﹣x₂|+|y₁﹣y₂|；例如：图1中，点M（﹣1，1）与点N（1，﹣2）之间的折线距离为d（M，N）=|﹣1﹣1|+|1﹣（﹣2）|=2+3=5．

解决下列问题：

已知E（2，0），若F（﹣1，﹣2），求d（E，F）；

(4)、如图2，已知E（2，0），H（1，t），若d（E，H）=3，求t的值；

(5)、如图3，已知P（3，3），点Q在x轴上，且三角形OPQ的面积为3，求d（P，Q）．

查看试题解析
20. 在物理学中，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．
如图1，一束光线 $m$ 射到平面镜 $a$ 上，被 $a$ 反射后的光线为 $n$ ，则入射光线 $m$ 、反射光线 $n$ 与平面镜 $a$ 所夹的锐角 $∠ 1 = ∠ 2$ ．

(1)、【简单应用】
如图2，有一口井，已知入射光线 $a$ 与水平线 $O C$ 的夹角为 $40 °$ ，现放置平面镜 $M N$ ，可使反射光线 $b$ 正好垂直照射到井底（即射线 $b ⊥ O C$ ）， $M N$ 与水平线的夹角 $∠ M O C$ 的度数为．

(2)、【类比拓展】
如图3，有两块平面镜 $O M, O N$ ，且 $O M ⊥ O N$ ，入射光线 $A B$ 经过两次反射，得到反射光线 $C D$ ．由以上光的反射定律，可知入射角与反射角相等，进而可以推得他们的余角也相等，即： $∠ 1 = ∠ 2, ∠ 3 = ∠ 4$ ．在这样的条件下，求证： $A B ∥ C D$ ．

(3)、【尝试探究】
两块平面镜 $O M, O N$ ，且 $∠ M O N = α$ ，入射光线 $A B$ 经过两次反射，得到反射光线 $C D$ ．如图4，光线 $A B$ 与 $C D$ 相交于点 $E$ ，则 $∠ B E C$ 的度数是多少？（用含 $α$ 的式子表示）（三角形内角和 $180 °$ ）

查看试题解析