2023-2024学年人教版七年级下册期末数学全真模拟试卷(一)

试卷更新日期：2024-06-09 类型：期末考试

进入出卷网下载

一、选择题(本大题共10小题，每小题3分，满分30分.在每小题给出的四个选项中，只有一项是符合题目要求的. )

1. 在实数 $- \frac{π}{2}$ ， $- 3$ ， 1， $\sqrt{2}$ 中，最小的数是（）

A、 $- 3$ B、 $- \frac{π}{2}$ C、1 D、 $\sqrt{2}$

查看试题解析
2. 如图，直线AB是起跳线，脚印是小明跳落沙坑时留下的痕迹，已知 $P A = 2.7$ 米， $M C = 2.6$ 米，则小明跳远的成绩可能是（）

A、2.7米 B、2.65米 C、2.6米 D、2.5米

查看试题解析
3. 如图，已知 $A B$ // $D E$ ， $∠ A B C = 75 °$ ， $∠ C D E = 150 °$ ，则∠BCD的度数为（）

A、55° B、45° C、60° D、50°

查看试题解析
4. 下列说法：①过一点有且只有一条直线与已知直线垂直；②过一点有且只有一条直线与这条直线平行；③过直线l外一点P向这条直线作垂线，这条垂线段就是点P到直线l的距离；④两个角的两边分别平行，则这两个角相等或互补；⑤无理数都是无限小数.其中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 已知点 $M$ 在第二象限，它到 $x$ 轴的距离为2，到 $y$ 轴的距离为3，则点 $M$ 的坐标是（）

A、 $(2, - 3)$ B、 $(3, - 2)$ C、 $(- 3, 2)$ D、 $(- 2, 3)$

查看试题解析
6. 某校课外小组的学生准备分组外出活动，若每组7人，则余下3人；若每组8人，则最后一组少5人，设课外小组的人数为x ，分成的组数为y ．依题意可得方程组为（）

A、 ${\begin{array}{l} 7 y = x - 3 \\ 8 y = x - 5 \end{array}$ B、 ${\begin{array}{l} 7 y = x - 3 \\ 8 y = x + 5 \end{array}$ C、 ${\begin{array}{l} 7 y = x + 3 \\ 8 y = x + 5 \end{array}$ D、 ${\begin{array}{l} 7 y = x + 3 \\ 8 y = x - 5 \end{array}$

查看试题解析
7. 已知命题“关于的不等式 $\{\begin{cases} x + 3 \leq 5 \\ x - 1 > k \end{cases}$ 无解”，能说明这个命题是假命题的一个反例可以是（）

A、 $k = - 1$ B、 $k = 1$ C、 $k = 1.2$ D、 $k = 2$

查看试题解析
8. 在一次绿色环保知识竞赛中，共有20道题，对于每一道题，答对得10分，答错或不答扣5分，则至少答对多少道题，得分才不低于80分?设答对 $x$ 道题，则可列不等式为( )

A、 $10 x - 5 (20 - x) \geq 80$ B、 $10 x + 5 (20 - x) \geq 80$ C、 $10 x - 5 (20 - x) > 80$ D、 $10 x + 5 (20 - x) > 80$

查看试题解析
9. 为了解某市七年级学生的视力情况，调查小组从中随机调查了 500 名学生的视力，下列说法正确的是( )

A、某市七年级学生是总体
B、每一名七年级学生是个体
C、500 名七年级学生是总体的一个样本
D、样本容量是 500

查看试题解析

二、填空题（本大题共6小题，每小题3分，满分18分.）

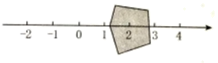
10. 如图，将数 $- \sqrt{5}$ ， $\sqrt{7}$ ， $\sqrt{13}$ 表示在数轴上，其中能被墨迹覆盖的数是．

查看试题解析
11. 如图，将 $△ A B C$ 沿 $B C$ 方向平移到 $△ D E F$ ，若A ， D之间的距离为2， $C E = 3$ ，则 $B F$ 的长度为。

查看试题解析
12. 在平面直角坐标系中，若有两点 $A (x_{1}, y_{1})$ ， $B (x_{2}, y_{2})$ ，利用平移知识可得到线段AB中点的坐标为 $(\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})$ ．
请利用以上结论解决问题：若点 $E (a, b)$ ， $F (b, a - b)$ ，线段EF的中点M恰好位于y轴上，且到x轴的距离是3，则点E的坐标为．

查看试题解析
13. 若 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 是二元一次方程 $a x + b y = - \frac{1}{2}$ 的一个解，则 $6 a - 4 b + 2025$ 的值为.

查看试题解析
14. 已知关于 $x ， y$ 的二元一次方程组 $\{\begin{array}{l} a_{1} x + b_{1} y = c_{1} \\ a_{2} x + b_{2} y = c_{2} \end{array}$ ，的解为 $\{\begin{array}{l} x = 2 \\ y = 1 \end{array}$ ，则关于 $x ， y$ 的二元一次方程组 $\{\begin{array}{l} a_{1} (x + 3) + b_{1} y - 2 b_{1} = c_{1} \\ a_{2} (x + 3) + b_{2} y - 2 b_{2} = c_{2} \end{array}$ 的解为

查看试题解析

三、解答题(本大题共8小题，满分72分.解答应写出文字说明、证明过程或演算步骤.)

15. 计算：

(1)、计算： $| \sqrt{3} - 2 | - \sqrt[3]{- 27} - \sqrt{(- 3)^{2}} + \sqrt{16}$

(2)、解方程组： ${\begin{array}{l} 6 x + 5 y = 31 ， ① \\ 3 x + 2 y = 13 ； ② \end{array}$

查看试题解析
16. 如图，直线 $A B$ 、 $C D$ 相交于点O ， $O A$ 平分 $∠ E O C$ ．

(1)、若 $∠ B O D = 35 °$ ，求 $∠ E O C$ 的度数；

(2)、若 $∠ E O C : ∠ E O D = 1 : 4$ ，求 $∠ B O D$ 的度数．

查看试题解析

17. 某校为加强学生安全意识，组织了全校800名学生参加安全知识竞赛，从中抽取了部分学生成绩（得分取正整数，满分为100分）进行统计．请根据尚未完成的频率分布表和频数分布直方图解题．

分数段	频数	频率
50.5-60.5	16	0.08
60.5-70.5	40	0.2
70.5-80.5	50	0.25
80.5-90.5	$m$	0.35
90.5-100.5	24	$n$

(1)、这次抽取了名学生的竞赛成绩进行统计，其中：

m =

，

n =

．

(2)、补全频数分布直方图．

(3)、若成绩在80分以下（含80分）的学生为安全意识不强，有待进一步加强安全教育，则该校安全意识不强的学生约有多少人？

查看试题解析

18. 为鼓励居民节约用电，广州市自2012年以来对家庭用电收费实行阶梯电价，即每月对每户居民的用电量分为三个档级收费，第一档为用电量在180千瓦时（含180千瓦时）以内的部分，执行基本价格；第二档为用电量在180千瓦时到450千瓦时（含450千瓦时）的部分，实行提高电价；第三档为用电量超出450千瓦时的部分，比第二档的单价每千瓦时提高0.05元．海珠区的李白同学家今年2月份用电330千瓦时，电费为213元，3月份用电240千瓦时，电费为150元．已知我市的另一位居民杜甫家今年4、5月份的家庭用电量分别为200和 490千瓦时，请你依据题目条件，计算杜甫家4、5月份的电费分别为多少元？

查看试题解析

19. 某公司有

A

、

B

两种型号的客车共20辆，它们的载客量、每天的租金如表所示．已知在20辆客车都坐满的情况下，共载客720人．

	$A$ 型号客车	$B$ 型号客车
载客量（人/辆）	45	30
租金（元/辆）	600	450

(1)、求

A

、B两种型号的客车各有多少辆？

(2)、某中学计划租用

A

、

B

两种型号的客车共8辆，送七年级师生到惠东伟鸿教育基地参加社会实践活动，已知该中学租车的总费用不超过4600元．求最多能租用多少辆

A

型号客车？

(3)、在（2）的条件下，若七年级的师生共有295人，请写出所有可能的租车方案，并确定最省钱的租车方案．

查看试题解析

20. 如图1，已知 $a ∥ b$ ，点 $A 、 B$ 在直线 $a$ 上，点 $C 、 D$ 在直线 $b$ 上，且 $A D ⊥ B C$ 于 $E$ ．

(1)、求证： $∠ A B C + ∠ A D C = 90 °$ ；

(2)、如图2， $B F$ 平分 $∠ A B C$ 交 $A D$ 于点 $F$ ， $D G$ 平分 $∠ A D C$ 交 $B C$ 于点 $G$ ，求 $∠ A F B + ∠ C G D$ 的度数；

(3)、如图3， $P$ 为线段 $A B$ 上一点， $I$ 为线段 $B C$ 上一点，连接 $P I$ ， $N$ 为 $∠ I P B$ 的角平分线 $P M$ 上一点，且 $∠ N C D = \frac{1}{2} ∠ B C N$ ，直接写出 $∠ C I P 、 ∠ I P N 、 ∠ C N P$ 之间的数量关系．

查看试题解析