广西梧州市长洲区2023年中考数学三模试卷

试卷更新日期：2024-06-07 类型：中考模拟

进入出卷网下载

一、选择题（共12小题，满分36分，每小题3分）

1. ﹣3的相反数是（　　）

A、3 B、 $\frac{1}{3}$ C、﹣3 D、- $\frac{1}{3}$

查看试题解析
2. 下列图形中，既是轴对称又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. “绿水青山就是金山银山”．某地积极响应党中央号召，大力推进农村厕所革命，已经累计投资1.102×10⁸元资金．数据1.102×10⁸的原数为（　　）

A、1102亿 B、1.102亿 C、110.2亿 D、11.02亿

查看试题解析
4. 下列运算正确的是（　　）

A、a³+a²＝a⁵ B、（a⁴）²＝a⁸ C、a⁶÷a²＝a³ D、﹣3（a﹣b）＝﹣3a﹣3b

查看试题解析
5. 在平面直角坐标系中，点P（m²+1，2）关于原点对称的点在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 如图，一根直尺 $E F$ 压在三角板 $30 °$ 的角 $∠ B A C$ 上，欲使 $C B ∥ E F$ ，则应使 $∠ F M B$ 的度数为（　　）

A、 $120 °$ B、 $100 °$ C、 $110 °$ D、 $130 °$

查看试题解析
7. 已知关于x的一元二次方程（k﹣1）x²﹣2x+1＝0有两个不相等的实数根，则k的取值范围是（　　）

A、k＜﹣2 B、k＜2 C、k＞2 D、k＜2且k≠1

查看试题解析
8. 下列事件中属于必然事件的是（）

A、一个奇数与一个偶数的和为奇数 B、一个三角形三个内角的和小于180° C、任意抛一枚均匀的硬币，正面朝上 D、有一匹马奔跑的速度是70米/秒

查看试题解析
9. 《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等．交易其一，金轻十三两．问金、银一枚各重几何？”．意思是：今有甲种袋子中装有黄金9枚（每枚黄金重量相同），乙种袋子中装有白银11枚（每枚白银重量相同），称重两袋相等．两袋互相交换1枚后，甲种袋子比乙种袋子轻了13两（袋子重量忽略不计）．问黄金、白银每枚各重多少两？设每枚黄金重x两，每枚白银重y两，则可建立方程为（　　）

A、 $\{\begin{array}{l} 11 x = 9 y \\ (8 x + y) + (10 y + x) = 13 \end{array}$ B、 $\{\begin{array}{l} 11 x = 9 y \\ (10 y + x) - (8 x + y) = 13 \end{array}$ C、 $\{\begin{array}{l} 9 x = 11 y \\ (10 y + x) - (8 x + y) = 13 \end{array}$ D、 $\{\begin{array}{l} 9 x = 11 y \\ (8 x + y) + (10 y + x) = 13 \end{array}$

查看试题解析
10. 如图，△ABC内接于⊙O ， ∠B＝65°，∠C＝70°．若BC＝3 $\sqrt{2}$ 则弧BC的长为（　　）

A、 $\frac{3}{4} π$ π B、 $\frac{3}{2} π$ C、 $\frac{9}{2} π$ D、 $3 \sqrt{2}$ π

查看试题解析
11. 如图，小刚骑电动车到单位上班，最初以某一速度匀速行进，途中由于遇到火车挡道，停下等待放行，耽误了几分钟，为了按时到单位，小刚加快了速度，仍保持匀速行进，结果准时到单位．小刚行进的路程y(千米）与行进时间t(小时）的函数图象的示意图，你认为正确的是（）

A、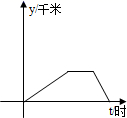 B、 C、 D、

查看试题解析
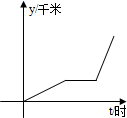12. 得天独厚的自然条件和生态资源，已让铜仁这片黔东沃土孕育出33个地理标志产品．在2023梵净山国际地理标志研讨会议召开之际，某区举行地理标志产品知识竞赛，如图使用 S_矩形_ABCO、S_矩_DEFO、S_矩形_GHIO、S_矩形_JKLO 分别描述了甲、乙、丙、丁四个社区居民竞赛成绩的优秀人数，已知y表示社区居民竞赛成绩的优秀率，x表示该社区参赛居民人数，点B和点K在同一条反比例函数图象上，则这四个社区在这次知识竞赛中优秀人数最多的是（　　）

A、甲 B、乙 C、丙 D、丁

查看试题解析

二、填空题（共6小题，满分12分，每小题2分）

13. 若二次根式 $\sqrt{5 a + 3}$ 是最简二次根式，则正整数a的最小值是．

查看试题解析
14. 当x＝时，分式 $\frac{x^{2} - 4}{x^{2} - 2 x}$ 的值为零.

查看试题解析
15. 如图，为了测量河宽AB（假设河的两岸平行），在河的彼岸选择一点A ，在点C测得∠ACB为30°，点D处测得∠ADB为60°，若CD＝60m ，则河宽AB为 m（结果保留根号）．

查看试题解析
16. 甲、乙两射击运动员10次射击训练的平均成绩恰好都是8.5环，方差分别是S_甲²＝0.85，S_乙²＝1.45，则在本次测试中，运动员的成绩更稳定（填“甲”或“乙”）．

查看试题解析
17. 已知A（x₁ ， y₁）、B（x₂ ， y₂）是一次函数y＝kx+2的图象上的不同两个点，（x₁﹣x₂）（y₁﹣y₂）＞0时，k的取值范围是．

查看试题解析
18. 如图 $\hat{A B}$ 所对圆心角∠AOB＝90°，半径为4，C是OB的中点，D是 $\hat{A B}$ 上一点，把CD绕点C逆时针旋转90°得到CE ，连接AE ，则AE的最小值是．

查看试题解析

三、解答题（共8小题，满分72分）

19. 计算： $(\sqrt{2})^{- 2} - 2 s i n 30^{\circ} - (π - 3)^{0} + |- \sqrt{\frac{1}{3}}|$ ．

查看试题解析
20. 先化简，再求值 $(a + 1 - \frac{3}{a - 1}) \div \frac{a^{2} + 4 a + 4}{a - 1}$ ，其中a＝2

查看试题解析
21. 老师给同学们布置了一个在平面内找一点，使该点到等腰三角形的三个顶点的距离相等”的尺规作图任务：
下面是小聪同学设计的尺规作图过程：
已知：如图，△ABC中，AB＝AC ．
求作：一点P ，使得PA＝PB＝PC ．
作法：
①作∠BAC的平分线AM交BC于点D；
②作边AB的垂直平分线EF ， EF与AM相交于点P；
③连接PB ， PC ．
所以，点P就是所求作的点
根据小聪同学设计的尺规作图过程，

(1)、使用直尺和圆规，补全图形．（保留作图痕迹）

(2)、完成下面的证明．
证明：∵AB＝AC ， AM平分∠BAC交BC于点D ，
∴AD是BC的垂直平分线：（　▲）（填推理依据）
∴PB＝PC ．
∵EF垂直平分AB ，交AM于点P ，
∴PA＝PB：（　▲）（填推理依据）
∴PA＝PB＝PC ．

(3)、过点D作DG⊥AB ， DH⊥AC ，垂足分别为G ， H ．
∵AD平分∠BAC ，
∴　▲＝　▲（　▲）（填推理的依据）．

查看试题解析
22. 如图，一次函数y＝kx+b（k≠0）与反比例函数 $y = \frac{m}{x}$ （m≠0）的图象交于二、四象限内的A、B两点，与x轴交于C点．过点B作BD⊥x轴，垂足为D ，若OB＝5，OD＝3，且点A的横坐标为﹣4．

(1)、求该反比例函数和一次函数的解析式；

(2)、求△AOC的面积．

(3)、直接写出满足 $k x + b ⩾ \frac{m}{x}$ 的x的取值范围．

查看试题解析
23. 某校为了了解全校400名学生参加课外锻炼的情况，随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查，结果如下：（单位：分）
40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36 34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45
分组
频数
频率
14.5﹣22.5
2
0.050
22.5﹣30.5
3
____
30.5﹣38.5
10
0.250
38.5﹣46.5
19
____
46.5﹣54.5
5
0.125
54.5﹣62.5
1
0.025
合计
40
1.00

(1)、补全频率分布表和频率分布直方图．

(2)、填空：在这个问题中，总体是，样本是．由统计结果分析得，这组数据的平均数是38.35（分），众数是，中位数是．

(3)、估计该校400名学生中，一周内平均每天参加课外锻炼时间在46.5分以上（含46.5分）的同学有多少人？

查看试题解析
24. 小明为班级购买信息学编程竞赛的奖品后，回学校向班主任李老师汇报说：“我买了两种书，共30本，单价分别为20元和24元，买书前我领了700元，现在还余38元. ” 李老师算了一下，说：“你肯定搞错了. ”

(1)、李老师为什么说他搞错了？试用方程的知识给予解释；

(2)、小明连忙拿出购物发票，发现的确弄错了，因为他还买了一个笔记本. 但笔记本的单价已模糊不清，只能辨认出应为小于10元的整数，如果单价为20元的书多于24元的书，请问：笔记本的单价为多少元？

查看试题解析
25. 在 $R t △ A B C$ 中， $A B = A C = 3$ ， $∠ B A C = 90 °$ ，点 $D$ 为边 $B C$ 的中点，以 $C D$ 为一边作正方形 $C D E F$ ，

(1)、如图1，点E恰好与点A重合，则线段BE与AF的数量关系为；

(2)、在（1）的条件下，
①如果正方形 $C D E F$ 绕点 $C$ 旋转，连接 $B E$ 、 $C E$ 、 $A F$ ，线段 $B E$ 与AF的数量关系有无变化？请仅就图2的情形给出证明；

②正方形 $C D E F$ 绕点 $C$ 旋转的过程中，当以点A，B，C，E为顶点的四边形是平行四边形时.直接写出线段AF的长.

查看试题解析
26. 如图，在平面直角坐标系中，抛物线y＝ax²+bx+c的图象与x轴交于A、B两点（点A在点B的左边），与y轴交于点C ，点A的坐标为（﹣1，0），抛物线顶点D的坐标为（1，﹣4），直线BC与对称轴相交于点E ．

(1)、求抛物线的解析式；

(2)、点M为直线x＝1右方抛物线上的一点（点M不与点B重合），设点M的横坐标为m ，记A、B、C、M四点所构成的四边形面积为S ，若S＝3S_△_BCD ，请求出m的值；

(3)、点P是线段BD上的动点，将△DEP沿边EP翻折得到△D'EP ，是否存在点P ，使得△D'EP与△BEP的重叠部分图形为直角三角形？若存在，请直接写出BP的长，若不存在，请说明理由．

查看试题解析

分组	频数	频率
14.5﹣22.5	2	0.050
22.5﹣30.5	3	____
30.5﹣38.5	10	0.250
38.5﹣46.5	19	____
46.5﹣54.5	5	0.125
54.5﹣62.5	1	0.025
合计	40	1.00