四川省乐山市犍为县2024年中考数学模拟预测试卷

试卷更新日期：2024-06-06 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1. 如图，为测量一棵与地面垂直的树OA的高度，在距离树的底端30米的B处，测得树顶A的仰角∠ABO为α，则树OA的高度为（）

A、 $\frac{30}{\tan α}$ 米 B、30sinα米 C、30tanα米 D、30cosα米

查看试题解析
2. 若抛物线y＝kx²﹣2x﹣1与x轴有两个不同的交点，则k的取值范围为（）

A、k＞﹣1 B、k≥﹣1 C、k＞﹣1且k≠0 D、k≥﹣1且k≠0

查看试题解析
3. 下列计算，正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{(- 2) \times (- 2)} = 2$ C、 $3 \sqrt{2} - \sqrt{2} = 3$ D、 $\sqrt{8} + \sqrt{2} = \sqrt{10}$

查看试题解析
4. “a是实数，|a|≥0”这一事件是（）

A、必然事件 B、不确定事件 C、不可能事件 D、随机事件

查看试题解析
5.
图1是边长为1的六个小正方形组成的图形，它可以围成图2的正方体，则图1中正方形顶点A、B在围成的正方体中的距离是（　　）

A、0 B、1 C、 $\sqrt{2}$ D、 $\sqrt{3}$

查看试题解析
6. 若函数 $y = \frac{2}{x}$ 与y=﹣2x﹣4的图象的交点坐标为（a，b），则 $\frac{1}{a} + \frac{2}{b}$ 的值是（　　）

A、﹣4 B、﹣2 C、1 D、2

查看试题解析
7. 如图，在平面直角坐标系中Rt△ABC的斜边BC在x轴上，点B坐标为（1，0），AC=2，∠ABC=30°，把Rt△ABC先绕B点顺时针旋转180°，然后再向下平移2个单位，则A点的对应点A^'的坐标为（　　）

A、（﹣4，﹣2﹣ $\sqrt{3}$ ） B、（﹣4，﹣2+ $\sqrt{3}$ ） C、（﹣2，﹣2+ $\sqrt{3}$ ） D、（﹣2，﹣2﹣ $\sqrt{3}$ ）

查看试题解析
8. 黄河是中华民族的象征，被誉为母亲河，黄河壶口瀑布位于我省吉县城西45千米处，是黄河上最具气势的自然景观．其落差约30米，年平均流量1010立方米/秒．若以小时作时间单位，则其年平均流量可用科学记数法表示为（）

A、6.06×10⁴立方米/时 B、3.136×10⁶立方米/时 C、3.636×10⁶立方米/时 D、36.36×10⁵立方米/时

查看试题解析
9. 如图，两个同心圆(圆心相同半径不同的圆)的半径分别为6cm和3cm，大圆的弦AB与小圆相切，则劣弧AB的长为( )

A、2πcm B、4πcm C、6πcm D、8πcm

查看试题解析
10. 下列算式的运算结果正确的是（　　）

A、m³•m²=m⁶ B、m⁵÷m³=m²（m≠0） C、（m^﹣2）³=m^﹣5 D、m⁴﹣m²=m²

查看试题解析
11. 等腰三角形底角与顶角之间的函数关系是（）

A、正比例函数 B、一次函数 C、反比例函数 D、二次函数

查看试题解析
12. 如图，在矩形ABCD中，AB=5，BC=7，点E为BC上一动点，把△ABE沿AE折叠，当点B的对应点B^'落在∠ADC的角平分线上时，则点B^'到BC的距离为（）

A、1或2 B、2或3 C、3或4 D、4或5

查看试题解析

二、填空题：（本大题共6个小题，每小题4分，共24分．）

13. 如图△ABC中，∠C=90°，AC=8cm，AB的垂直平分线MN交AC于D，连接BD，若cos∠BDC= $\frac{3}{5}$ ，则BC的长为．

查看试题解析
14. 如图，将三角形AOC绕点O顺时针旋转120°得三角形BOD ，已知OA=4，OC=1，那么图中阴影部分的面积为．（结果保留π）

查看试题解析
15. 数学的美无处不在．数学家们研究发现，弹拨琴弦发出声音的音调高低，取决于弦的长度，绷得一样紧的几根弦，如果长度的比能够表示成整数的比，发出的声音就比较和谐．例如，三根弦长度之比是15：12：10，把它们绷得一样紧，用同样的力弹拨，它们将分别发出很调和的乐声do、mi、so，研究15、12、10这三个数的倒数发现： $\frac{1}{12} - \frac{1}{15} = \frac{1}{10} - \frac{1}{12}$ ．我们称15、12、10这三个数为一组调和数．现有一组调和数：x，5，3（x＞5），则x的值是．

查看试题解析
16. 如图，是由大小完全相同的正六边形组成的图形，小军准备用红色、黄色、蓝色随机给每个正六边形分别涂上其中的一种颜色，则上方的正六边形涂红色的概率是．

查看试题解析
17. 2018年5月13日，中国首艘国产航空母舰首次执行海上试航任务，其排水量超过6万吨，将数60000用科学记数法表示应为.

查看试题解析
18. 关于x的不等式组 ${\begin{array}{l} 2 x + a > 0 \\ x - 1 \leq \frac{x - 1}{3} \end{array}$ 的整数解有4个，那么a的取值范围( )

A、4＜a＜6 B、4≤a＜6 C、4＜a≤6 D、2＜a≤4

查看试题解析

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．

19. 如图，在△ABC中，∠C＝90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．

(1)、求证：△ACD≌△AED；

(2)、若∠B＝30°，CD＝1，求BD的长．

查看试题解析
20.

(1)、关于 $x$ 的一元二次方程 $x^{2} - 3 x + k = 0$ 有实数根．求 $k$ 的取值范围；

(2)、如果 $k$ 是符合条件的最大整数，且一元二次方程 $(m - 1) x^{2} + x + m - 3 = 0$ 与方程 $x^{2} - 3 x + k = 0$ 有一个相同的根，求此时 $m$ 的值．

查看试题解析
21. 某楼盘2018年2月份准备以每平方米7500元的均价对外销售，由于国家有关房地产的新政策出台后，购房者持币观望，为了加快资金周转，房地产开发商对价格连续两个月进行下调，4 月份下调到每平方米6075元的均价开盘销售．

(1)、求3、4两月平均每月下调的百分率；

(2)、小颖家现在准备以每平方米6075元的开盘均价，购买一套100平方米的房子，因为她家一次性付清购房款，开发商还给予以下两种优惠方案以供选择：①打9.8折销售；②不打折，送两年物业管理费，物业管理费是每平方米每月1.5元，小颖家选择哪种方案更优惠？

(3)、如果房价继续回落，按此平均下调的百分率，请你预测到6月份该楼盘商品房成交均价是否会跌破4800元/平方米，请说明理由．

查看试题解析
22.
如图，△ABC是等边三角形，AO⊥BC，垂足为点O，⊙O与AC相切于点D，BE⊥AB交AC的延长线于点E，与⊙O相交于G、F两点．

(1)、求证：AB与⊙O相切；

(2)、若等边三角形ABC的边长是4，求线段BF的长？

查看试题解析
23. 在“母亲节”期间，某校部分团员参加社会公益活动，准备购进一批许愿瓶进行
销售，并将所得利润捐给慈善机构．根据市场调查，这种许愿瓶一段时间内的销售量y(个)于销售单价x(元/个)之间的对应关系如图所示．

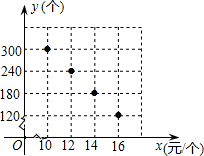(1)、试判断y与x之间的函数关系，并求出函数关系式；

(2)、若许愿瓶的进价为6元/个，按照上述市场调查销售规律，求利润w(元)与销售单价x(元/个)之间的
函数关系式；

(3)、若许愿瓶的进货成本不超过900元，要想获得最大利润，试求此时这种许愿瓶的销售单价，并求出
最大利润

查看试题解析
24. 在 $R t Δ A B C$ 中， $∠ A C B = 9 0^{∘}$ ， $C D$ 是 $A B$ 边的中线， $D E ⊥ B C$ 于 $E$ ，连结 $C D$ ，点 $P$ 在射线 $C B$ 上（与 $B$ ， $C$ 不重合）

(1)、如果 $∠ A = 3 0^{∘}$
①如图1， $∠ D C B =$ ▲ $^{∘}$
②如图2，点 $P$ 在线段 $C B$ 上，连结 $D P$ ，将线段 $D P$ 绕点 $D$ 逆时针旋转 $6 0^{∘}$ ，得到线段 $D F$ ，连结 $B F$ ，补全图2猜想 $C P$ 、 $B F$ 之间的数量关系，并证明你的结论；

(2)、如图3，若点 $P$ 在线段 $C B$ 的延长线上，且 $∠ A = α (0^{∘} < α < 9 0^{∘})$ ，连结 $D P$ ，将线段 $D P$ 绕点逆时针旋转 $2 α$ 得到线段 $D F$ ，连结 $B F$ ，请直接写出 $D E$ 、 $B F$ 、 $B P$ 三者的数量关系（不需证明）

查看试题解析
25. 如图，在直角坐标系中△ABC的A、B、C三点坐标A（7，1）、B（8，2）、C（9，0）．

(1)、请在图中画出△ABC的一个以点P（12，0）为位似中心，相似比为3的位似图形△A^'B^'C^'（要求与△ABC同在P点一侧），画出△A^'B^'C^'关于y轴对称的△A^''B^''C^''；

(2)、写出点A'的坐标．

查看试题解析
26. 如图，方格纸中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．在图中画出以线段AB为一边的矩形ABCD（不是正方形），且点C和点D均在小正方形的顶点上；在图中画出以线段AB为一腰，底边长为2 $\sqrt{2}$ 的等腰三角形ABE，点E在小正方形的顶点上，连接CE，请直接写出线段CE的长．

查看试题解析
27. 如图，建筑物BC上有一旗杆AB ，从与BC相距40m的D处观测旗杆顶部A的仰角为50°，观测旗杆底部B的仰角为45°，求旗杆AB的高度．（参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）

查看试题解析