2024年北师大版数学八年级第二学期期末模拟试卷二

试卷更新日期：2024-06-06 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列等式从左到右的变形中，属于因式分解的是（）

A、 $(x + 1) (x - 1) = x^{2} - 1$ B、 $x^{2} + 2 x + 1 = (x + 1)^{2}$ C、 $x^{2} + 2 x - 1 = x (x + 2) - 1$ D、 $x (x - 1) = x^{2} - x$

查看试题解析
2. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）

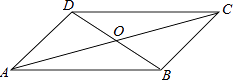A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB∥DC，AD=BC

查看试题解析
3. 将 $\frac{a b}{2 a + 5 b}$ 中的 $a ， b$ 都扩大4倍，则分式的值（）

A、不变 B、扩大 $4$ 倍 C、扩大 $8$ 倍 D、扩大 $16$ 倍

查看试题解析
4. 已知关于x的不等式组 ${\begin{array}{l} 3 x - m > 0 \\ x - 1 \leq 5 \end{array}$ 有四个整数解，则m的取值范围是（）

A、 $6 \leq m < 9$ B、 $6 < m \leq 9$ C、 $6 < m < 9$ D、 $6 \leq m \leq 9$

查看试题解析
5. 如图，将△ABC绕点A顺时针旋转角α（0°＜α＜180°），得到△AED ，若AC＝1，CE＝ $\sqrt{2}$ ，则α的度数为（）

A、30° B、45° C、60° D、90°

查看试题解析
6. 化简（ab+b²）÷ $\frac{a^{2} - b^{2}}{a}$ 的结果是（　　）

A、 $\frac{a b}{a - b}$ B、 $\frac{a b}{a + b}$ C、 $\frac{b}{a - b}$ D、 $\frac{b}{a + b}$

查看试题解析
7. 电商经济的蓬勃发展，物流配送体系建设的不断完善，推动我国快递行业迅速崛起．某快递公司的甲、乙两名快递员从公司出发分别到距离公司2400米和1000米的两地派送快件，甲快递员的速度是乙快递员速度的1.2倍，乙快递员比甲快递员提前10分钟到达派送地点．若设乙快递员的速度是x米/分，则下列方程正确的是（）

A、 $\frac{2400}{1.2 x} - \frac{1000}{x} = 10$ B、 $\frac{1.2 x}{2400} - \frac{x}{1000} = 10$ C、 $\frac{1000}{1.2 x} - \frac{2400}{x} = 10$ D、 $\frac{1000}{x} - \frac{2400}{1.2 x} = 10$

查看试题解析
8. 已知四边形ABCD是平行四边形，对角线AC、BD交于点O，E是BC的中点，以下说法错误的是（）

A、OE= $\frac{1}{2}$ DC B、OA=OC C、∠BOE=∠OBA D、∠OBE=∠OCE

查看试题解析
9. 若分式方程 $\frac{x}{x - 1} - \frac{m}{1 - x} = 2$ 有增根，则m的值为（　　）

A、1 B、 $- 1$ C、2 D、 $- 2$

查看试题解析
10. 如图，在△ABC中，∠C＝90°，线段AB的垂直平分线交BC于点D ，连结AD ．若CD＝1，BD＝2，则AC的长为（）

A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{3}{2}$

查看试题解析

二、填空题（每题3分，共18分）

11. 若分式 $\frac{\sqrt{x + 3}}{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
12. 分解因式： $a^{3} - {4ab}^{2} =$ .

查看试题解析
13. 一次函数 $y_{1} = 4 x + 5$ 与 $y_{2} = 3 x + 10$ 的图像如图所示，则 $y_{1} > y_{2}$ 的解集是．

查看试题解析
14. 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次平移，每次移动一个单位，得到点A₁(0，1)，A₂(1，1)，A₃(1，0)，A₄(2，0)，…那么点A₂₀₂₂的坐标为.

查看试题解析
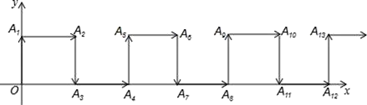15. 如图是由射线AB，BC，CD，DE，EF，FA组成的平面图形，则∠1+∠2+∠3+∠4+∠5+∠6=°．

查看试题解析
16. 如图，▱ABCD的顶点C在等边△BEF的边BF上，点E在AB的延长线上，G为DE的中点，连接CG．若AD＝5，AB＝CF＝3，则CG的长为．

查看试题解析

三、解答题（共10题，共72分）

17. 解不等式组 ${\begin{matrix} 2 x + 1 > x \\ \frac{x + 5}{2} - x \geq 1 \end{matrix}$ 并把解集在数轴上表示出来

查看试题解析
18. 解不等式组 $\{\begin{array}{l} 3 x - 1 < x + 5 \\ \frac{x - 3}{2} < x - 1 \end{array}$ ，把它的解集表示在数轴上，并求出这个不等式组的整数解．

查看试题解析
19. 先化简，再求值： $(1 - \frac{x + 1}{x}) \div \frac{x^{2} - 1}{x^{2} - x}$ ，其中 $x = \sqrt{2} - 1$ ．

查看试题解析
20. 先化简，再求值： $(a - 1 + \frac{2}{a + 1}) \div (a^{2} + 1)$ ，其中 $a = \sqrt{5} - 1$ .

查看试题解析
21. 解方程： $\frac{x - 2}{x - 1} - 2 = \frac{3}{x - 1}$ ．

查看试题解析
22. 解方程： $\frac{x - 1}{x + 1} - \frac{2}{x^{2} - 1} = 1$ ．

查看试题解析
23. 已知：如图，在四边形 $A B C D$ 中， $D E ⊥ A C ， B F ⊥ A C$ ，垂足分别为E ， F ，延长 $D E 、 B F$ ，分别交 $A B$ 于点H ，交 $B C$ 于点G ，若 $A D ∥ B C$ ， $A E = C F$ ．

(1)、求证：四边形 $A B C D$ 为平行四边形；

(2)、若 $∠ D A H = ∠ G B A ， G F = 2 ， C F = 4$ ，求 $A D$ 的长．

查看试题解析
24. 冰墩墩是2022年北京冬奥会的吉祥物，其敦厚、可爱的形象深入人心，制作的奥运纪念品很受大家喜爱。已知A型号的冰墩墩手办比B型号的冰墩墩钥匙扣的单价多30元，用880元购买A型号手办的数量是用290元购买B型号钥匙扣数量的2倍．

(1)、求A，B两种型号纪念品的单价分别是多少元？

(2)、若计划购买A，B两种型号的纪念品共100个，且所花费用不超过6800元，求最多能购买多少个A型号的纪念品？

查看试题解析
25.

(1)、回归课本
请用文字语言表述三角形的中位线定理：．

(2)、回顾证法
证明三角形中位线定理的方法很多，但多数都要通过添加辅助线构图完成．下面是其中一种辅助线的添加方法．请结合图2，补全求证及证明过程．
已知：在 $△ A B C$ 中，点D ， E分别是 $A B, A C$ 的中点．
求证：_▲_．
证明：过点 $C$ 作 $C F / / A B$ ，与 $D E$ 的延长线交于点 $F$ ．

(3)、实践应用
如图3，点 $B$ 和点 $C$ 被池塘隔开，在 $B C$ 外选一点 $A$ ，连接 $A B, A C$ ，分别取 $A B, A C$ 的中点D ， E ，测得 $D E$ 的长度为9米，则B ， C两点间的距离为．

查看试题解析
26. 如图，在Rt△ABC中，∠C＝90°，BC＝8，AC＝6，动点P从点A开始，沿边AC向点C以每秒1个单位长度的速度运动，动点D从点A开始，沿边AB向点B以每秒 $\frac{5}{3}$ 个单位长度的速度运动，且恰好能始终保持连结两动点的直线PD⊥AC，动点Q从点C开始，沿边CB向点B以每秒2个单位长度的速度运动，连结PQ．点P，D，Q分别从点A，C同时出发，当其中一点到达端点时，另两个点也随之停止运动，设运动时间为t秒（t≥0）．

(1)、当t=3时，求PD的长？

(2)、当t为何值时，四边形BQPD的面积为△ABC面积的一半？

(3)、是否存在t的值，使四边形PDBQ为平行四边形？若存在，求出t的值；若不存在，说明理由．

查看试题解析