贵州省贵阳市2023-2024学年八年级下学期数学期末考试仿真试卷
试卷更新日期:2024-06-06 类型:期末考试
一、选择题
-
1. 不等式 的解集在数轴上表示为( )A、
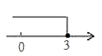 B、
B、 C、
C、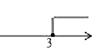 D、
D、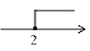 2. 下列分式是最简分式的是( )A、 B、 C、 D、3. 已知一个多边形的内角和等于外角和的3倍,则这个多边形为( )A、五边形 B、六边形 C、七边形 D、八边形4. 设□△○表示三种不同的物体,用天平比较它们质量的大小,情况如图,那么这三种物体按质量从大到小的顺序为( )
2. 下列分式是最简分式的是( )A、 B、 C、 D、3. 已知一个多边形的内角和等于外角和的3倍,则这个多边形为( )A、五边形 B、六边形 C、七边形 D、八边形4. 设□△○表示三种不同的物体,用天平比较它们质量的大小,情况如图,那么这三种物体按质量从大到小的顺序为( ) A、□△○ B、□○△ C、△○□ D、△□○5. 如图,一次函数的图象与轴交于点 , 则不等式的解集为( )
A、□△○ B、□○△ C、△○□ D、△□○5. 如图,一次函数的图象与轴交于点 , 则不等式的解集为( ) A、 B、 C、 D、6. 如图,盒内长、宽、高分别是6cm、3cm、2cm,盒内可放木棒最长的长度是( )
A、 B、 C、 D、6. 如图,盒内长、宽、高分别是6cm、3cm、2cm,盒内可放木棒最长的长度是( ) A、6cm B、7cm C、8cm D、9cm7. 若关于x的方程有增根,则m的值为( )A、0 B、1 C、-1 D、28. 如图,在中, , 斜边的垂直平分线交于点 , 交于点 , , 则的长度为( )
A、6cm B、7cm C、8cm D、9cm7. 若关于x的方程有增根,则m的值为( )A、0 B、1 C、-1 D、28. 如图,在中, , 斜边的垂直平分线交于点 , 交于点 , , 则的长度为( ) A、 B、 C、 D、9. 小李家装饰地面,已有正三角形形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则小李不应购买的地砖形状是( )A、正方形 B、正六边形 C、正八边形 D、正十二边形10. 如图,在Rt△ABC中,分别为CA、CB的中点,AF平分 , 交DE于点 , 若 , 则的长为( )
A、 B、 C、 D、9. 小李家装饰地面,已有正三角形形状的地砖,现打算购买另一种不同形状的正多边形地砖,与正三角形地砖在同一顶点处作平面镶嵌,则小李不应购买的地砖形状是( )A、正方形 B、正六边形 C、正八边形 D、正十二边形10. 如图,在Rt△ABC中,分别为CA、CB的中点,AF平分 , 交DE于点 , 若 , 则的长为( ) A、1 B、 C、2 D、
A、1 B、 C、2 D、二、填空题
-
11. 分解因式: .12. 关于x不等式组有且仅有3个整数解,则a的取值范围是.13. 如图, , 的坐标为 , , 若将线段平移至 , 则的值为 .
 14. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:
14. 如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,得到下列四个结论:
①AD和EF互相垂直平分;
②AE=AF;
③当∠BAC=90°时,AD=EF;
④DE是AB的垂直平分线.
其中正确的是(填序号).
三、解答题
-
15. 解不等式组.16. 先化简: , 并从 , , 中选一个合适的数作为的值代入求值.17.
在平面直角坐标系中,△ABC的点坐标分别是A(2,4)、B(1,2)、C(5,3),如图:
(1)以点(0,0)为旋转中心,将△ABC顺时针转动90°,得到△A1B1C1 , 在坐标系中画出△A1B1C1 , 写出A1、B1、C1的坐标;
(2)在(1)中,若△ABC上有一点P(m,n),直接写出对应点P1的坐标.
 18. 如图,在中, , 直线经过顶点 , 过 , 两点分别作的垂线 , , , 为垂足,且 . 求证:
18. 如图,在中, , 直线经过顶点 , 过 , 两点分别作的垂线 , , , 为垂足,且 . 求证: (1)、;(2)、 .19. 如图,在平行四边形ABCD中,E,F是直线BD上的两点,DE=BF.
(1)、;(2)、 .19. 如图,在平行四边形ABCD中,E,F是直线BD上的两点,DE=BF. (1)、求证:四边形AECF是平行四边形;(2)、若AD⊥BD,AB=5,BC=3,且EF-AF=2,求DE的长.20. 某商场进货员预测一种应季T恤衫能畅销市场,就用4 000元购进一批这种T恤衫,面市后果然供不应求.商场又用8 800元购进了第二批这种T恤衫,所购数量是第一批购进量的 2倍,但每件的进价贵了4元.(1)、该商场购进第一批、第二批T恤衫每件的进价分别是多少元?(2)、如果两批T恤衫按相同的标价销售,最后缺码的40件T恤衫按
(1)、求证:四边形AECF是平行四边形;(2)、若AD⊥BD,AB=5,BC=3,且EF-AF=2,求DE的长.20. 某商场进货员预测一种应季T恤衫能畅销市场,就用4 000元购进一批这种T恤衫,面市后果然供不应求.商场又用8 800元购进了第二批这种T恤衫,所购数量是第一批购进量的 2倍,但每件的进价贵了4元.(1)、该商场购进第一批、第二批T恤衫每件的进价分别是多少元?(2)、如果两批T恤衫按相同的标价销售,最后缺码的40件T恤衫按7折优惠售出,要使两批T恤衫全部售完后利润率不低于80%(不考虑其他因素),那么每件T恤衫的标价至少是多少元?
21. 问题:如图①,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45°,试判断BE,EF,FD之间的数量关系. (1)、【发现证明】
(1)、【发现证明】小聪把△ABE绕点A逆时针旋转90°至△ADG的位置,从而发现EF=BE+FD,请你利用图①证明上述结论.
(2)、【类比引申】如图②,在四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E,F分别在边BC,CD上,则当∠EAF与∠BAD满足关系时,仍有EF=BE+FD.请说明理由.
(3)、【探究应用】如图③,在某公园的同一水平面上,四条通道围成四边形ABCD.已知AB=AD=80 m,∠B=60°,∠ADC=120°,∠BAD=150°,道路BC,CD上分别有景点E,F,且AE⊥AD,DF=40( -1)m,现要在E,F之间修一条笔直的道路,求这条道路EF的长(结果精确到1 m,参考数据: ≈1.41, ≈1.73).