2024年北师大版数学八年级第二学期期末模拟试卷一

试卷更新日期：2024-06-06 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 要使分式 $\frac{1}{x + 3}$ 有意义，x应满足的条件是（　　）

A、 $x > - 3$ B、 $x < - 3$ C、 $x \neq - 3$ D、 $x = - 3$

查看试题解析
2. 下列从左边到右边的变形，属于因式分解的是（）

A、 $6 a^{2} b^{2} = 3 a b \cdot 2 a b$ B、 $(x + 1) (x - 1) = x^{2} - 1$ C、 $x^{2} - 4 x + 4 = (x - 2)^{2}$ D、 $x^{2} - x - 4 = x (x - 1) - 2$

查看试题解析
3. 在四边形ABCD中，AB∥CD且AB=CD，若∠B=56°，则∠C的度数是（）

A、56° B、65° C、114° D、124°

查看试题解析
4. 下列判断不正确的是（）

A、若 $a > b$ ，则 $- 4 a < - 4 b$ B、若 $2 a > 3 a$ ，则 $a < 0$ C、若 $a > b$ ，则 $a c^{2} > b c^{2}$ D、若 $a c^{2} > b c^{2}$ ，则 $a > b$

查看试题解析
5. 如图，在平面直角坐标系中，将四边形ABCD先向下平移，再向右平移得到四边形A'B'C'D' ．若点A、B、A'的坐标分别为（-3，5），（-4，3），（3，3），则点B'的坐标为（）

A、（1，2） B、（2，1） C、（1，4） D、（4，1）

查看试题解析
6. 下列可以用完全平方公式因式分解的是（）

A、4a²-4a-1 B、4a²＋2a＋1 C、1-4a＋4a² D、2a²＋4a＋1

查看试题解析
7. 计算 $\frac{x}{a + 1} \cdot \frac{a^{2} - 1}{2 x}$ 的结果正确的是（）

A、 $\frac{a - 1}{2}$ B、 $\frac{a + 1}{2}$ C、 $\frac{a - 1}{2 x}$ D、 $\frac{a + 1}{2 a + 2}$

查看试题解析
8. 解一元一次方程的一般步骤包括：去分母、去括号、移项、合并同类项、系数化 $1$ 等 $.$ 将一元一次方程 $\frac{x + 1}{2} - 1 = \frac{x}{3}$ 去分母，得（）

A、 $3 (x + 1) - 6 = 2 x$ B、 $3 (x + 1) - 1 = 2 x$
C、 $3 x + 1 - 1 = 2 x$ D、 $2 (x + 1) - 6 = 3 x$

查看试题解析
9. 如图，EF过平行四边形ABCD对角线的交点O，交AD于点E，交BC于点F，若平行四边形ABCD的周长为36，OE＝3，则四边形EFCD的周长为（　　）

A、28 B、26 C、24 D、20

查看试题解析
10. 若关于x的分式方程 $\frac{2}{x - 1} + \frac{m x}{(x - 1) (x + 2)} = \frac{1}{x + 2}$ 有增根，则m的值为（）

A、1.5 B、-6 C、1或-2 D、1.5或-6

查看试题解析

二、填空题（每题3分，共18分）

11. 因式分解： $3 a^{2} - 12 =$ .

查看试题解析
12. 一个正多边形的内角和为 $540 °$ ，则这个正多边形的每一个外角等于度．

查看试题解析
13. 已知关于x的分式方程 $\frac{x}{x - 1} - 2 = \frac{k}{1 - x}$ 的解为非负数，则k的取值范围为．

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中， $B D$ 是对角线，E ， F是对角线上的两点，要使四边形 $A F C E$ 是平行四边形，还需添加一个条件（只需添加一个）是．

查看试题解析
15. 如图，在菱形ABCD中，∠B＝45°，E、F分别是边CD，BC上的动点，连接AE、EF，G、H分别为AE、EF的中点，连接GH．若GH的最小值为3，则BC的长为．

查看试题解析
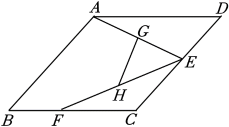16. 如图，在△ABC中，EF是AB边的垂直平分线，AC=18cm，BC=16cm，则△BCE的周长为 cm．

查看试题解析

三、解答题（共9题，共72分）

17. 解不等式组 ${\begin{array}{l} 3 x + 2 < 2 (x + 2) ①, \\ \frac{x - 1}{2} \leq \frac{2 x - 1}{3} ②, \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
18. 先化简再求值： $(a + 2 - \frac{5}{a - 2}) \div \frac{a^{2} + 6 a + 9}{a - 2}$ ，其 $a$ 从 $- 2$ ， 2， $- 3$ ， 3中选一个合适的数代入求值．

查看试题解析
19.

(1)、先化简： $(1 - \frac{1}{m - 1}) \div \frac{m^{2} - 4 m + 4}{m^{2} - m}$ ，再从 $- 1 \leq m \leq 2$ 中选合适的整数代入求值.

(2)、解分式方程： $\frac{x + 1}{x} + \frac{1}{x - 2} = 1$ .

查看试题解析
20. 若关于x的方程 $\frac{x - 2 a}{x - 3} + \frac{2 a}{3 - x} = 2$ 的解为非负数，求a的取值范围．

查看试题解析
21. 如图，在 $△ A B C$ 中， $D E$ 为 $B C$ 边上的垂直平分线，与 $∠ B A C$ 的平分线交于点E ，过点E作 $E F ⊥ A B$ ，交 $A B$ 的延长线于点F ，作 $E G ⊥ A C$ 于点G.

(1)、求证： $B F = C G$ .

(2)、若 $A B = 6$ ， $A C = 15$ ，求 $C G$ 的长.

查看试题解析
22. 如图，点E ， F是平行四边形 $A B C D$ 对角线 $A C$ 上的两点，且 $A E = C F$ .

(1)、求证：四边形 $B E D F$ 是平行四边形；

(2)、若 $A B ⊥ B F$ ， $A B = 16$ ， $B F = 12$ ， $A C = 24$ .求线段 $E F$ 的长.

查看试题解析
23. 先阅读下面的材料，再解决问题：
因式分解多项式：am+an+bm+bn，
先把它的前两项分成一组，并提出a；把它的后两项分成一组，并提出b：
得：a（m+n）+b（m+n）
再提公因式（m+n），得：（m+n）（a+b）．
于是得到：am+an+bm+bn＝a（m+n）+b（m+n）＝（a+b）（m+n）．
这种因式分解的方法叫做分组分解法．
请用上面材料中提供的方法解决问题：

(1)、将多项式ab﹣ac+b²﹣bc分解因式；

(2)、若△ABC的三边a、b、c满足条件：a⁴﹣b⁴+a²c²+b²c²＝0，试判断△ABC的形状．

查看试题解析
24. 普陀山佛茶又称佛顶山云雾茶，具有提神解乏之功效和一定的药用价值．深圳某茶店用32000元购进A等级茶叶若干盒，用6000元购进B等级茶叶若干盒，所购A等级茶叶比B等级茶叶多10盒，已知A等级茶叶的每盒进价是B等级茶叶每盒进价的4倍．

(1)、A，B两种等级茶叶的每盒进价分别为多少元？

(2)、当购进的所有茶叶全部售完后，茶店以相同的进价再次购进A，B两种等级茶叶共60盒，但购茶的总预算控制在36000元以内，若A等级茶叶的售价是每盒900元，B等级茶叶的售价为每盒250元，则A，B两种等级茶叶分别购进多少盒时可使获利润最大？最大利润是多少？

查看试题解析
25. 将一副直角三角板按图1方式叠放在一起，并且直角顶点C重合，其中 $∠ B = 30 °$ ， $∠ D = 45 °$ ．保持三角尺 $A B C$ 固定不动，将三角尺 $C D E$ 绕着点C顺时针旋转α度．探究以下问题：

(1)、如图2，当 $α = 210 °$ 时，求证： $A B ∥ E C$ ；

(2)、当 $0 ° < α < 180 °$ 时，若这两个三角尺的一组边互相平行，请画出相应的图形，并求出此时α的度数．

查看试题解析