新疆维吾尔自治区2024年中考数学二模试卷
试卷更新日期:2024-06-05 类型:中考模拟
一、选择题(本大题共9小题,每小题4分,共36分)
-
1. 预计到2025年,我国5G用户数将超过900000000,将900000000用科学记数法表示为( )A、 B、 C、 D、2. 某几何体的三视图如图所示,则该几何体为( )
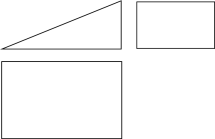 A、
A、 B、
B、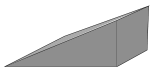 C、
C、 D、
D、 3. 如图,数轴上表示实数的点可能是( )
3. 如图,数轴上表示实数的点可能是( )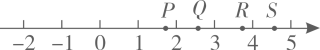 A、点P B、点Q C、点R D、点S4. 一次函数的图象不经过第( )象限.A、四 B、三 C、二 D、一5. 计算( ) , 正确的结果是( )A、16 B、42 C、 D、6. 方程(x-3)(x+1)=x-3的解是 ( )A、x=0 B、x=3 C、x=3或x=-1 D、x=3或x=07. 如图,内接于 , , , 的半径为2,则图中阴影部分的面积是( )
A、点P B、点Q C、点R D、点S4. 一次函数的图象不经过第( )象限.A、四 B、三 C、二 D、一5. 计算( ) , 正确的结果是( )A、16 B、42 C、 D、6. 方程(x-3)(x+1)=x-3的解是 ( )A、x=0 B、x=3 C、x=3或x=-1 D、x=3或x=07. 如图,内接于 , , , 的半径为2,则图中阴影部分的面积是( ) A、 B、 C、 D、8. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )
A、 B、 C、 D、8. 如图,矩形中, , 以点B为圆心,适当长为半径画弧,分别交 , 于点E,F,再分别以点E,F为圆心,大于长为半径画弧交于点P,作射线 , 过点C作的垂线分别交于点M,N,则的长为( )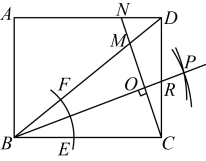 A、 B、 C、 D、49. 如图1,正方形的边长为4,为边的中点.动点从点出发沿匀速运动,运动到点时停止.设点的运动路程为 , 线段的长为 , 与的函数图象如图2所示,则点的坐标为( )
A、 B、 C、 D、49. 如图1,正方形的边长为4,为边的中点.动点从点出发沿匀速运动,运动到点时停止.设点的运动路程为 , 线段的长为 , 与的函数图象如图2所示,则点的坐标为( )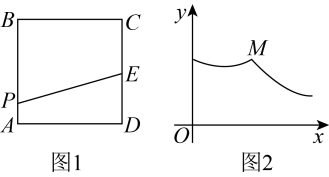 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,每小题4分,共24分)
-
10. 若代数式有意义,则实数的取值范围是 .11. 一个多边形的内角和是720°,那么这个多边形是 边形.12. 从1,-3,2,-4四个数中任选两个数组成一个坐标,则坐标在第二象限的概率为 .13. 如图,在中, , , 点在上且 , 连结 , 则.
 14. 如图,的顶点在第一象限,顶点在轴上,反比例函数的图象经过点 , 若 , 的面积为10,则的值为 .
14. 如图,的顶点在第一象限,顶点在轴上,反比例函数的图象经过点 , 若 , 的面积为10,则的值为 . 15. 如图,把一个边长为的菱形沿着直线折叠,使点与延长线上的点重合,交于点 , 交延长线于点 , 交于点 , 于点 , , 下列四个结论:①;②;③;④其中正确的结论序号是.
15. 如图,把一个边长为的菱形沿着直线折叠,使点与延长线上的点重合,交于点 , 交延长线于点 , 交于点 , 于点 , , 下列四个结论:①;②;③;④其中正确的结论序号是.
三、解答题(本大题共8小题,共90分.解答应写出必要的文字说明、证明过程或演算步骤)
-
16.(1)、计算:.(2)、解方程:.17.(1)、解不等式组:(2)、某学校为进一步开展好劳动教育实践活动,用1580元购进A,B两种劳动工具共145件,A,B两种劳动工具每件分别为10元,12元.求购进A,B两种劳动工具的件数分别是多少?18. 已知:如图,中,是中点,连接 , 延长线交的延长线于点 , 连接 .
 (1)、求证:;(2)、若 , , 判断四边形的形状,并证明你的结论.19. “防溺水”是校园安全教育工作
(1)、求证:;(2)、若 , , 判断四边形的形状,并证明你的结论.19. “防溺水”是校园安全教育工作 重点之一.某校为确保学生安全,开展了“远离溺水•珍爱生命”的防溺水安全知识竞赛.现从七年级、八年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
重点之一.某校为确保学生安全,开展了“远离溺水•珍爱生命”的防溺水安全知识竞赛.现从七年级、八年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:七年级:92,75,82,96,84,90,85,97,85,92,68,100,85,86,95,85,89,90,91,93.
八年级:90,87,93,97,90,84,92,72,100,80,90,91,59,93,87,90,82,91,92,100.
【整理与分析数据】
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
七年级
0
1
1
8
a
八年级
1
0
1
5
13
【应用数据】
平均数
众数
中位数
七年级
88
85
b
八年级
88
c
90
(1)、由上表填空:a= , b= , c=;(2)、若成绩不低于90分为优秀等次,该校七、八年级共有学生1600人,请你估计两个年级在本次竞赛中获得优秀等次的共有多少人?(3)、你认为哪个年级的学生对防溺水安全知识掌握的总体水平较好,请从两个不同的角度说明理由.20. 某数学小组要测量学校路灯的顶部到地面的距离,他们借助皮尺、测角仪进行测量,在B处测得路灯顶部P的仰角 , D处测得路灯顶部P的仰角 , 已知 . 测角仪的高度为 , 路灯顶部到地面的距离PE约为多少米?(结果精确到0.1米.参考数据: , , , )
 21. 共享电动车是一种新理念下的交通工具:主要面向~的出行距离.现有、两种品牌的共享电动车,收费与骑行时间之间的函数关系如图所示,其中品牌收费方式对应 , 品牌的收费方式对应 .
21. 共享电动车是一种新理念下的交通工具:主要面向~的出行距离.现有、两种品牌的共享电动车,收费与骑行时间之间的函数关系如图所示,其中品牌收费方式对应 , 品牌的收费方式对应 . (1)、品牌每分钟收费元;(2)、求品牌的函数关系式;(3)、如果小明每天早上需要骑行品牌或品牌的共享电动车去工厂上班,已知两种品牌共享电动车的平均行驶速度均为 , 小明家到工厂的距离为 , 那么小明选择哪个品牌的共享电动车更省钱呢?22. 如图, 是 ABC的外接圆,AB为直径,∠BAC的平分线交 于点D,过点D作DE AC分别交AC、AB的延长线于点E、F.
(1)、品牌每分钟收费元;(2)、求品牌的函数关系式;(3)、如果小明每天早上需要骑行品牌或品牌的共享电动车去工厂上班,已知两种品牌共享电动车的平均行驶速度均为 , 小明家到工厂的距离为 , 那么小明选择哪个品牌的共享电动车更省钱呢?22. 如图, 是 ABC的外接圆,AB为直径,∠BAC的平分线交 于点D,过点D作DE AC分别交AC、AB的延长线于点E、F. (1)、求证:EF是 的切线;(2)、若AC=4,CE=2,求 的长度.(结果保留 )23. 综合与探究
(1)、求证:EF是 的切线;(2)、若AC=4,CE=2,求 的长度.(结果保留 )23. 综合与探究如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),与y轴交于C(0,﹣3)点,点P是直线BC下方的抛物线上一动点.
 (1)、求这个二次函数的表达式.(2)、当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.(3)、连接PO、PC,并把△POC沿CO翻折,得到四边形POP'C,那么是否存在点P,使四边形POP'C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(1)、求这个二次函数的表达式.(2)、当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.(3)、连接PO、PC,并把△POC沿CO翻折,得到四边形POP'C,那么是否存在点P,使四边形POP'C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.