湖南省岳阳市平江县2024年中考数学二模试卷
试卷更新日期:2024-06-05 类型:中考模拟
一、选择题(在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项.本大题共10个小题,每小题3分,共30分)
-
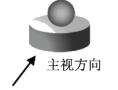
1. 在 , 0, , 2这四个实数中,最大的数是( )A、0 B、 C、2 D、2. 根据有关部门测算,2024年春节假期7天,全国国内旅游出游251000000人次.数据251000000用科学记数法表示为( )A、 B、 C、 D、3. 如图所示几何体是由一个球体和一个圆柱组成的,它的俯视图是( )
 A、
A、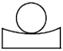 B、
B、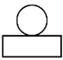 C、
C、 D、
D、 4. 不等式组的解集在数轴上表示正确的是( )A、
4. 不等式组的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 5. 以下调查中,适合全面调查的是( ).A、了解全国中学生的视力情况 B、检测“神舟十六号”飞船的零部件 C、检测台州的城市空气质量 D、调查某池塘中现有鱼的数量6. 在如图所示的电路中,随机闭合开关 , , 中的两个,能让红灯发光的概率是( )
5. 以下调查中,适合全面调查的是( ).A、了解全国中学生的视力情况 B、检测“神舟十六号”飞船的零部件 C、检测台州的城市空气质量 D、调查某池塘中现有鱼的数量6. 在如图所示的电路中,随机闭合开关 , , 中的两个,能让红灯发光的概率是( ) A、 B、 C、 D、7. 如图,在中,点D在边AB上,过点D作 , 交AC点E . 若 , , 则的值是( )
A、 B、 C、 D、7. 如图,在中,点D在边AB上,过点D作 , 交AC点E . 若 , , 则的值是( ) A、 B、 C、 D、8. 如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为的函数图象.根据这个函数的图象,下列说法正确的是( )
A、 B、 C、 D、8. 如图所示,小英同学根据学习函数的经验,自主尝试在平面直角坐标系中画出了一个解析式为的函数图象.根据这个函数的图象,下列说法正确的是( ) A、图象与x轴没有交点 B、当时 C、函数图象关于原点成中心对称 D、y随x的增大而减小9. 如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A , B , C , D , 连接AB , 则的度数为( )
A、图象与x轴没有交点 B、当时 C、函数图象关于原点成中心对称 D、y随x的增大而减小9. 如图,将一个量角器与一把无刻度直尺水平摆放,直尺的长边与量角器的外弧分别交于点A , B , C , D , 连接AB , 则的度数为( ) A、 B、 C、 D、10. 已知二次函数(其中x是自变量),当时对应的函数值y均为正数,则a的取值范围为( )A、 B、或 C、或 D、或
A、 B、 C、 D、10. 已知二次函数(其中x是自变量),当时对应的函数值y均为正数,则a的取值范围为( )A、 B、或 C、或 D、或二、填空题(本大题共8小题,每小题3分,共24分)
-
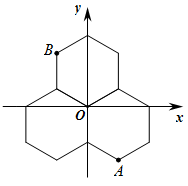
11. 二次根式在实数范围内有意义,则实数x的取值范围是 .12. 分解因式: .13. 三个能够重合的正六边形的位置如图.已知B点的坐标是 , 则A点的坐标是 .
 14. 如图,在中, , 点M是斜边BC的中点,以AM为边作正方形AMEF . 若 , 则 .
14. 如图,在中, , 点M是斜边BC的中点,以AM为边作正方形AMEF . 若 , 则 . 15. 如图,在四边形ABCD中, , , . 按下列步骤作图:①以点D为圆心,适当长度为半径画弧,分别交DA , DC于E , F两点;②分别以点E , F为圆心以大于的长为半径画弧,两弧交于点P;③连接DP并延长交BC于点G . 则BG的长是 .
15. 如图,在四边形ABCD中, , , . 按下列步骤作图:①以点D为圆心,适当长度为半径画弧,分别交DA , DC于E , F两点;②分别以点E , F为圆心以大于的长为半径画弧,两弧交于点P;③连接DP并延长交BC于点G . 则BG的长是 . 16. 正偶数2,4,6,8,10,…,按如下规律排列,
16. 正偶数2,4,6,8,10,…,按如下规律排列,
则第27行的第21个数是 .
17. 甲、乙两个工程组同时挖掘沈白高铁某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务,甲、乙两组挖掘的长度之和与甲组挖掘时间x(天)之间的关系如图所示.则乙组每天挖掘m. 18. 如图,两个全等的矩形纸片重叠在一起,矩形的长和宽分别是4和3,则重叠部分的四边形ABCD中的对角线BD的长是 .
18. 如图,两个全等的矩形纸片重叠在一起,矩形的长和宽分别是4和3,则重叠部分的四边形ABCD中的对角线BD的长是 .
三、解答题(本大题共8小题,共66分,第19-20题每小题6分,第21-22题每小题8分,第22-23题每小题9分,第25-26题10分)
-
19. 计算:20. 已知 , 计算的值21. 为了解A、B两款品质相近的智能玩具飞机在一次充满电后运行的最长时间,有关人员分别随机调查了A、B两款智能玩具飞机各10架,记录下它们运行的最长时间(分钟),并对数据进行整理、描述和分析(运行最长时间用x表示,共分为三组:合格 , 中等 , 优等),下面给出了部分信息:
A款智能玩具飞机10架一次充满电后运行最长时间是:
60,64,67,69,71,71,72,72,72,82.
B款智能玩具飞机10架一次充满电后运行最长时间属于中等的数据是:
70,71,72,72,73.
两款智能玩具飞机运行最长时间统计表
类别
A
B
平均数
70
70
中位数
71
b
众数
a
67
方差
30.4
26.6
 (1)、上述图表中 , , ;(2)、根据以上数据,你认为哪款智能玩具飞机运行性能更好?请说明理由(写出一条理由即可);(3)、若某玩具仓库有A款智能玩具飞机200架、B款智能玩具飞机120架,估计两款智能玩具飞机运行性能在中等及以上的共有多少架?22. 某实践探究小组想测得湖边两处的距离,数据勘测组通过勘测,得到了如下记录表:
(1)、上述图表中 , , ;(2)、根据以上数据,你认为哪款智能玩具飞机运行性能更好?请说明理由(写出一条理由即可);(3)、若某玩具仓库有A款智能玩具飞机200架、B款智能玩具飞机120架,估计两款智能玩具飞机运行性能在中等及以上的共有多少架?22. 某实践探究小组想测得湖边两处的距离,数据勘测组通过勘测,得到了如下记录表:实践探究活动记录表
活动内容
测量湖边A、B两处的距离
成员
组长:×××
组员:××××××××××××
测量工具
测角仪,皮尺等
测量示意图

说明:因为湖边A、B两处的距离无法直接测量,数据勘测组在湖边找了一处位置C . 可测量C处到A、B两处的距离.通过测角仪可测得、、的度数.
测量数据
角的度数
边的长度
米
米
数据处理组得到上面数据以后做了认真分析.他们发现不需要勘测组的全部数据就可以计算出A、B之间的距离.于是数据处理组写出了以下过程,请补全内容.
已知:如图,在中, , . ▲ . (从记录表中再选一个条件填入横线)

求:线段AB的长.(为减小结果的误差,若有需要,取1.41,取1.73,取2.45进行计算,最后结果保留整数.)
23. 已知为的直径, , C为上一点,连接 . (1)、如图①,若C为的中点,求的大小和的长;(2)、如图②,若为的半径,且 , 垂足为E,过点D作的切线,与的延长线相交于点F,求的长.24. 今年五一小长假期间,我市迎来了一个短期旅游高峰.某热门景点的门票价格规定见下表:
(1)、如图①,若C为的中点,求的大小和的长;(2)、如图②,若为的半径,且 , 垂足为E,过点D作的切线,与的延长线相交于点F,求的长.24. 今年五一小长假期间,我市迎来了一个短期旅游高峰.某热门景点的门票价格规定见下表:票的种类
A
B
C
购票人数(人)
100以上
票价(元)
50
45
40
某旅行社接待的甲、乙两个旅游团共102人(甲团人数多于乙团),在打算购买门票时,如果把两团联合作为一个团体购票会比两团分别各自购票节省730元.
(1)、求两个旅游团各有多少人?(2)、一个人数不足50人的旅游团,当游客人数最低为多少人时,购买B种门票比购买A种门票节省?25. 综合与实践【问题情境】:数学活动课上,王老师给同学们每人发了一张等腰三角形纸片探究折叠的性质.
已知 , , 点E为AC上一动点,将以BE为对称轴翻折.同学们经过思考后进行如下探究:

【独立思考】:小明:“当点D落在BC上时, . ”
小红:“若点E为AC中点,给出AC与DC的长,就可求出BE的长.”
【实践探究】:奋进小组的同学们经过探究后提出问题1,请你回答:
问题1:在等腰中, , , 由翻折得到.
(1)、如图1,当点D落在BC上时,求证:;(2)、如图2,若点E为AC中点, , , 求BE的长.【问题解决】:小明经过探究发现:若将问题1中的等腰三角形换成的等腰三角形,可以将问题进一步拓展.
问题2:如图3,在等腰中, , , . 若 , 则求BC的长.
26. 已知抛物线 . (1)、如图①,若抛物线图象与x轴交于点A(3,0),与y轴交点B(0,-3),连接AB .
(1)、如图①,若抛物线图象与x轴交于点A(3,0),与y轴交点B(0,-3),连接AB .(Ⅰ)求该抛物线所表示的二次函数表达式;
(Ⅱ)若点P是第四象限内抛物线上一动点,过点P作轴于点H , 与线段AB交于点M , 作轴于点K , 与线段AB交于点N , 求的最大值
(2)、如图②,直线与y轴交于点C , 同时与抛物线交于点D( , 0),以线段CD为边作菱形CDFE , 使点F落在x轴的正半轴上,若该抛物线与线段CE没有交点,求b的取值范围.