广西壮族自治区柳州市柳北区、鱼峰区2024年中考数学模拟试卷
试卷更新日期:2024-06-05 类型:中考模拟
一、单项选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡上对应题目的答案标号涂黑)
-
1. 全国深入践行习近平生态文明思想,科学开展大规模国土绿化行动,厚植美丽中国亮丽底色,去年完成造林约3830000公顷.用科学记数法表示3830000是( )A、 B、 C、 D、2. 下面四个手机应用图标中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算正确的是( )A、 B、 C、 D、4. 若二次根式在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、5. 如图,点A , B , C都在上,若 , 则为( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 若二次根式在实数范围内有意义,则x的取值范围是( )A、 B、 C、 D、5. 如图,点A , B , C都在上,若 , 则为( ) A、 B、 C、 D、6. 如图,从热气球A看一栋楼底部C的俯角是( )
A、 B、 C、 D、6. 如图,从热气球A看一栋楼底部C的俯角是( ) A、 B、 C、 D、7. 如图,和是以点O为位似中心的位似图形, , 的周长为8,则的周长为( )
A、 B、 C、 D、7. 如图,和是以点O为位似中心的位似图形, , 的周长为8,则的周长为( ) A、12 B、18 C、20 D、508. 如图是一个六边形质保徽章,该六边形的内角和是( )
A、12 B、18 C、20 D、508. 如图是一个六边形质保徽章,该六边形的内角和是( ) A、 B、 C、 D、9. 一组数据2,3,4,x,6的平均数是4,则x是( )A、2 B、3 C、4 D、510. 《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百九十一步,只云长阔共六十步,问长多阔几何?”意思是:一块矩形田地的面积为891平方步,只知道它的长与宽共60步,问它的长比宽多多少步?依题意得,长比宽多( )步.A、15 B、6 C、9 D、1211. 某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对 ,在坐标系中进行描点,则正确的是()A、
A、 B、 C、 D、9. 一组数据2,3,4,x,6的平均数是4,则x是( )A、2 B、3 C、4 D、510. 《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百九十一步,只云长阔共六十步,问长多阔几何?”意思是:一块矩形田地的面积为891平方步,只知道它的长与宽共60步,问它的长比宽多多少步?依题意得,长比宽多( )步.A、15 B、6 C、9 D、1211. 某项工作,已知每人每天完成的工作量相同,且一个人完成需12天.若m个人共同完成需n天,选取6组数对 ,在坐标系中进行描点,则正确的是()A、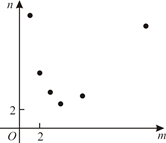 B、
B、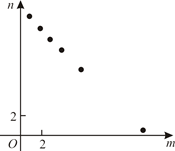 C、
C、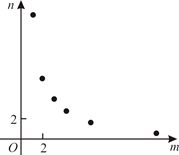 D、
D、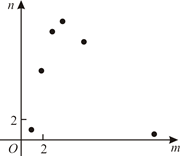 12. 如图,在平面直角坐标系中,矩形的对角线的中点与坐标原点重合,点E是x轴上一点,连接 . 若平分 , 反比例函数( , )的图象经过上的两点A , F , 且 , 的面积为18,则k的值为( )
12. 如图,在平面直角坐标系中,矩形的对角线的中点与坐标原点重合,点E是x轴上一点,连接 . 若平分 , 反比例函数( , )的图象经过上的两点A , F , 且 , 的面积为18,则k的值为( ) A、10 B、11 C、12 D、14
A、10 B、11 C、12 D、14二、填空题(本大题共6小题,每小题2分,共12分。)
-
13. 因式分解: = .14. 把二次函数的图象向下平移2个单位长度,平移后抛物线的解析式为 .15. 实数a,b在数轴上对应点的位置如图所示,则a.(填“>”“=”或“<”)
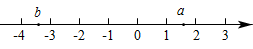 16. 将等腰直角三角板与量角器按如图所示的方式摆放,使三角板的直角顶点与量角器的中心O重合,且两条直角边分别与量角器边缘所在的弧交于A、B两点.若厘米,则的长度为厘米.(结果保留)
16. 将等腰直角三角板与量角器按如图所示的方式摆放,使三角板的直角顶点与量角器的中心O重合,且两条直角边分别与量角器边缘所在的弧交于A、B两点.若厘米,则的长度为厘米.(结果保留)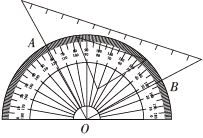 17. 如图,与斜坡垂直的太阳光线照射立柱(与水平地面垂直)形成的影子,一部分落在地面上,另一部分落在斜坡上.若米,米,斜坡的坡角 , 则立柱的高为米.(结果保留根号)
17. 如图,与斜坡垂直的太阳光线照射立柱(与水平地面垂直)形成的影子,一部分落在地面上,另一部分落在斜坡上.若米,米,斜坡的坡角 , 则立柱的高为米.(结果保留根号) 18. 已知二次函数 , 当时,此时函数的最小值是 .
18. 已知二次函数 , 当时,此时函数的最小值是 .三、解答题(本大题共8小题,共72分,解答应写出文字说明,证明过程或演算步骤。)
-
19. 计算: .20. 解方程: .21. 如图,四边形中, , , 于点 .
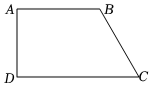 (1)、用尺规作的角平分线,交于点;不写作法,保留作图痕迹(2)、连接求证:四边形是菱形.22. 某日下午,某校组织学生观看“天宫课堂”第二课重播,跟着空间站的翟志刚、王亚平、叶光富三位宇航员学习科学知识,他们相互配合,生动演示了四个实验:(A)微重力环境下的太空“冰雪”实验,(B)液桥演示实验,(C)水油分离实验,(D)太空抛物实验.观看完后,该校对部分学生对四个实验的喜爱情况作了抽样调查,将调查情况制成了如下的条形统计图(图①)和扇形统计图(图②).
(1)、用尺规作的角平分线,交于点;不写作法,保留作图痕迹(2)、连接求证:四边形是菱形.22. 某日下午,某校组织学生观看“天宫课堂”第二课重播,跟着空间站的翟志刚、王亚平、叶光富三位宇航员学习科学知识,他们相互配合,生动演示了四个实验:(A)微重力环境下的太空“冰雪”实验,(B)液桥演示实验,(C)水油分离实验,(D)太空抛物实验.观看完后,该校对部分学生对四个实验的喜爱情况作了抽样调查,将调查情况制成了如下的条形统计图(图①)和扇形统计图(图②).
请根据图中信息,回答下列问题:
(1)、共调查了名学生,图2中A所对应的圆心角度数为;(2)、请补全条形统计图;(3)、若从两名男生、两名女生中随机抽取2人参加学校组织的“我爱科学”演讲比赛,请用列表或画树状图的方法,求抽到的学生恰好是一男一女的概率.23. 某集团有限公司生产甲乙两种电子产品共8万件,准备销往东南亚国家和地区.已知2件甲种电子产品与3件乙种电子产品的销售额相同;1件甲种电子产品比1件乙种电子产品的销售额多300元.(1)、求甲种电子产品与乙种电子产品销售单价各多少元?(2)、若使甲乙两种电子产品的销售总额不低于5400万元,则至少销售甲种电子产品多少万件?24. 如图,内接于 , P是的直径延长线上一点, , 过点O作的平行线交的延长线于点D . (1)、试判断直线与的位置关系,并说明理由;(2)、若 , , 求线段的长.25. 【综合与实践】
(1)、试判断直线与的位置关系,并说明理由;(2)、若 , , 求线段的长.25. 【综合与实践】【问题背景】
如图①,“漏刻”是我国古代一种利用水流计时的工具,古诗“金炉香尽漏声残,翦翦轻风阵阵寒”,描绘了“漏刻”不断漏水的情景.
如图②,综合实践小组用甲、乙两个透明的竖直放置的容器和一根装有节流阀(控制水的流速)的软管,制作了类似“漏刻”的简易计时装置.

【实验操作】上午 , 综合实践小组在甲容器里加满水,此时水面高度为 , 开始放水后,每隔记录一次甲容器中的水面高度,相关数据如表:
记录时间
流水时间
0
10
20
30
40
水面高度
30
29
28.1
27
25.8
【建立模型】小组讨论发现:“ , ”是初始状态下的准确数据,每隔水面高度值的变化不均匀,但可以用一次函数近似地刻画水面高度h与流水时间t的关系.
【问题解决】
(1)、利用时,;时,这两组数据求水面高度h与流水时间t的函数解析式;(2)、利用(1)中所求解析式,计算当甲容器中的水面高度为时是几点钟?(3)、经检验,发现有两组表中观察值不满足(1)中求出的函数解析式,存在偏差,小组决定优化函数解析式,减少偏差。通过查阅资料后知道:t为表中数据时,根据(1)中解析式求出所对应的函数值,计算这些函数值与对应h的观察值之差的平方和,记为w;w越小,偏差越小.请根据表中数据计算出(1)中得到的函数解析式的w值;26. 【探究与证明】如图,在四边形中,对角线与相交于点O , 记的面积为 , 的面积为 . (1)、【问题解决】如图①,若 , 求证:
(1)、【问题解决】如图①,若 , 求证:小红同学展示出如下正确的证明办法,请在横线上将内容补充完整.
证明:过点D作交于点E , 过点B作交于点F , 如图①所示:则
∴(填写位置关系)
∴;
∴;
∵;
;
∴ .
(2)、【探索推广】如图②,若与不平行,(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.(3)、【拓展应用】如图③,在上取一点E , 使 . 过点E作交于点F , 点H为的中点,交于点G , 且 , 若 , 求值.