初中数学同步训练必刷提高卷(北师大版七年级下册 第五单元测试卷)
试卷更新日期:2024-06-04 类型:单元试卷
一、选择题(每题3分,共30分)
-
1. 如图,在下列四个图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列四所世界名牌大学的校徽图案,是轴对称图形的个数是( )
2. 下列四所世界名牌大学的校徽图案,是轴对称图形的个数是( ) A、1个 B、2个 C、3个 D、4个3. 小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).A、
A、1个 B、2个 C、3个 D、4个3. 小王准备在红旗街道旁建一个送奶站,向居民区A,B提供牛奶,要使A,B两小区到送奶站的距离之和最小,则送奶站C的位置应该在( ).A、 B、
B、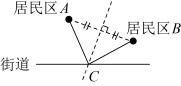 C、
C、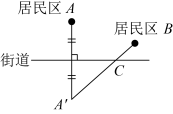 D、
D、 4. 如图,在中,点D , E分别在边 , 上,将沿折叠至的位置,点A的对应点为F . 若 , , 则的度数为( )
4. 如图,在中,点D , E分别在边 , 上,将沿折叠至的位置,点A的对应点为F . 若 , , 则的度数为( )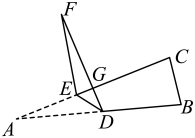 A、 B、 C、 D、5. 如图,三角形纸片 , 点是边上一点,连接 , 把沿着翻折,得到 , 与交于点 , 连接交于点 . 若 , , , 的面积为 , 则的长度为( )
A、 B、 C、 D、5. 如图,三角形纸片 , 点是边上一点,连接 , 把沿着翻折,得到 , 与交于点 , 连接交于点 . 若 , , , 的面积为 , 则的长度为( ) A、 B、1 C、 D、26. 如图,把一张上下边沿互相平行的纸条如图折叠,是折痕,若 , 则的度数是( )
A、 B、1 C、 D、26. 如图,把一张上下边沿互相平行的纸条如图折叠,是折痕,若 , 则的度数是( )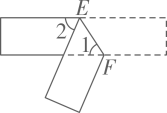 A、 B、 C、 D、7. 如图,将四边形纸片ABCD沿EF折叠,点A落在A1处,若∠1+∠2=90°,则∠A的度数是( )
A、 B、 C、 D、7. 如图,将四边形纸片ABCD沿EF折叠,点A落在A1处,若∠1+∠2=90°,则∠A的度数是( ) A、45° B、40° C、35° D、30°8. 如图,△ABC中边AB的垂直平分线分别交BC , AB于点D , E , AE=3cm , △ADC的周长为9cm , 则△ABC的周长是( )
A、45° B、40° C、35° D、30°8. 如图,△ABC中边AB的垂直平分线分别交BC , AB于点D , E , AE=3cm , △ADC的周长为9cm , 则△ABC的周长是( )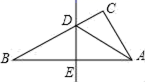 A、10cm B、12cm C、15cm D、17cm9. 如图,把一张长方形纸片ABCD折叠后,点C、点D的对应点分别为点C′和点D′,若∠1=48°,则∠2的度数为( )
A、10cm B、12cm C、15cm D、17cm9. 如图,把一张长方形纸片ABCD折叠后,点C、点D的对应点分别为点C′和点D′,若∠1=48°,则∠2的度数为( ) A、138° B、132° C、121° D、111°10. 图1是长方形纸条, , 将纸条沿折叠成折叠成图2,则图中的的度数是( )
A、138° B、132° C、121° D、111°10. 图1是长方形纸条, , 将纸条沿折叠成折叠成图2,则图中的的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(共4题,共20分)
-
11. 如图,射线AB与射线CD平行,点F为射线AB上的一定点,连接CF,点P是射线CD上的一个动点(不包括端点C),将 沿PF折叠,使点C落在点E处.若 ,当点E到点A的距离最大时, .
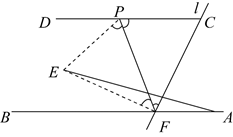 12. 如图所示的长方形纸条ABCD,将纸片沿MN折叠,MB与DN交于点K,若∠1=70°,则∠MKN=°.
12. 如图所示的长方形纸条ABCD,将纸片沿MN折叠,MB与DN交于点K,若∠1=70°,则∠MKN=°. 13. 如图,点N是四边形ABCD的DC边上一点,沿BN折叠四边形,使点C落在边AD上的点M处,再沿BM,NM折叠这个四边形,若点A,D恰好同时落在BN上的点P处,则的度数为°.
13. 如图,点N是四边形ABCD的DC边上一点,沿BN折叠四边形,使点C落在边AD上的点M处,再沿BM,NM折叠这个四边形,若点A,D恰好同时落在BN上的点P处,则的度数为°. 14. 如图,在等腰中, , , 是等边三角形,是的平分线上一动点,连接 , , 则的最小值为 .
14. 如图,在等腰中, , , 是等边三角形,是的平分线上一动点,连接 , , 则的最小值为 .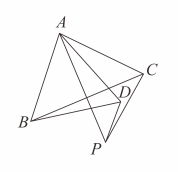 15. 如图,长方形纸片ABCD,M为AD边上一点,将纸片沿BM、CM折叠,使A点落在A1处,D点落在D1处,若∠AMB=35°,∠1=40°,则∠MCB的度数为°
15. 如图,长方形纸片ABCD,M为AD边上一点,将纸片沿BM、CM折叠,使A点落在A1处,D点落在D1处,若∠AMB=35°,∠1=40°,则∠MCB的度数为°
三、作图题(共2题,共10分)
-
16. 如图,以直线l为对称轴在网格中画出图形的另一半.
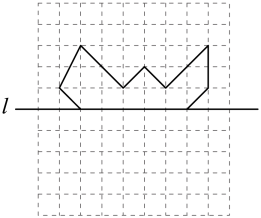 17. 如图,以虚线为对称轴在方格纸上画出图形的另一半.
17. 如图,以虚线为对称轴在方格纸上画出图形的另一半.
四、解答题(共2题,共10分)
-
18. 如图,把一个长方形纸片沿EF折叠后,点D、C分别落在点D'、C'的位置,且D'C'交BC于点M,若∠EFB=56°,求∠BMD'的度数.
 19. 如图,直线AD和CE是△ABC的两条对称轴,AD和CE相交于点O,OD与OE有什么数量关系?请说明理由.
19. 如图,直线AD和CE是△ABC的两条对称轴,AD和CE相交于点O,OD与OE有什么数量关系?请说明理由.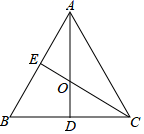
五、综合题(共3题,共30分)
-
20. 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(﹣2,﹣2).
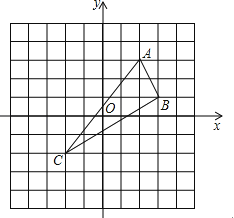 (1)、请在图中作出△ABC关于y轴的轴对称图形△DEF(A,B、C的对称点分别是D、E,F),并直接写出D、E、F的坐标.(2)、求△ABC的面积.21. 如图,在直角坐标系中有一个格点三角形ABC(顶点都在格点上的三角形),已知A(﹣2,1),B(﹣3,4),C(﹣4,1),直线MN过点M(2,5),N(5,2).
(1)、请在图中作出△ABC关于y轴的轴对称图形△DEF(A,B、C的对称点分别是D、E,F),并直接写出D、E、F的坐标.(2)、求△ABC的面积.21. 如图,在直角坐标系中有一个格点三角形ABC(顶点都在格点上的三角形),已知A(﹣2,1),B(﹣3,4),C(﹣4,1),直线MN过点M(2,5),N(5,2). (1)、请在图中作出格点三角形ABC关于x轴对称的格点三角形A′B′C′(A,B,C的对应点依次为A′,B′,C′);(2)、连结AM,AN,则tan∠MAN= .
(1)、请在图中作出格点三角形ABC关于x轴对称的格点三角形A′B′C′(A,B,C的对应点依次为A′,B′,C′);(2)、连结AM,AN,则tan∠MAN= .
22. 问题提出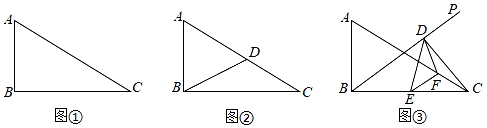 (1)、如图①,在Rt△ABC中,∠ABC=90°,AB=12,BC=16,则AC=;
(1)、如图①,在Rt△ABC中,∠ABC=90°,AB=12,BC=16,则AC=;问题探究
(2)、如图②,在Rt△ABC中,∠ABC=90°,AC=10,点D是AC边上一点,且满足DA=DB,则CD=;问题解决
(3)、如图③,在Rt△ABC中,过点B作射线BP,将∠C折叠,折痕为EF,其中E为BC中点,点F在AC边上,点C的对应点落在BP上的点D处,连接ED、FD,若BC=8,求△BCD面积的最大值,及面积最大时∠BCD的度数.