贵州省2023-2024学年八年级下学期数学期末考试仿真试卷(六)
试卷更新日期:2024-06-04 类型:期末考试
一、选择题
-
1. 下列扑克牌中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 八年级(1)班共有50名学生,体重最重为72千克,体重最轻为35千克,取组距为10,为统计该班学生的体重情况,可以将该班学生分为( )A、3组 B、4组 C、5组 D、6组4. 估计的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间5. 下列一次函数的图象经过第一、三、四象限的是( )A、 B、 C、 D、6. 如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件有( )
2. 下列计算正确的是( )A、 B、 C、 D、3. 八年级(1)班共有50名学生,体重最重为72千克,体重最轻为35千克,取组距为10,为统计该班学生的体重情况,可以将该班学生分为( )A、3组 B、4组 C、5组 D、6组4. 估计的值应在( )A、3和4之间 B、4和5之间 C、5和6之间 D、6和7之间5. 下列一次函数的图象经过第一、三、四象限的是( )A、 B、 C、 D、6. 如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件有( )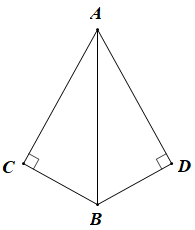 A、0个 B、1个 C、2个 D、3个7. 如图是小明、小刚小红做课间操时的位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,那么小红的位置可表示为( )
A、0个 B、1个 C、2个 D、3个7. 如图是小明、小刚小红做课间操时的位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,那么小红的位置可表示为( )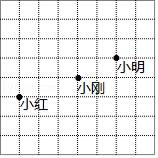 A、(1,3) B、(-2,3) C、(-1,3) D、(0,2)8. 《九章算术》提供了许多组勾股数,如 , , 等,并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究,得到如下规律:若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个整数构成一组勾股数;若m是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1得到两个整数,那么m与这两个整数构成一组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律,“由10生成的勾股数”的“弦数”为( )A、26 B、101 C、13 D、249. 点P(-1,2)是由点Q(0,-1)经过( )而得到的.A、先向右平移1个长度,再向下平移3个单位长度 B、先向左平移1个长度,再向下平移3个单位长度 C、先向上平移3个长度,再向左平移1个单位长度 D、先向下平移1个长度,再向右平移3个单位长度10. 如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是( )
A、(1,3) B、(-2,3) C、(-1,3) D、(0,2)8. 《九章算术》提供了许多组勾股数,如 , , 等,并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究,得到如下规律:若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个整数构成一组勾股数;若m是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1得到两个整数,那么m与这两个整数构成一组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律,“由10生成的勾股数”的“弦数”为( )A、26 B、101 C、13 D、249. 点P(-1,2)是由点Q(0,-1)经过( )而得到的.A、先向右平移1个长度,再向下平移3个单位长度 B、先向左平移1个长度,再向下平移3个单位长度 C、先向上平移3个长度,再向左平移1个单位长度 D、先向下平移1个长度,再向右平移3个单位长度10. 如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是( ) A、BP是∠ABC的平分线 B、AD=BD C、 D、CD=BD11. 如图,与均为直角三角形,且 , , , 点E是的中点,则的长为( )
A、BP是∠ABC的平分线 B、AD=BD C、 D、CD=BD11. 如图,与均为直角三角形,且 , , , 点E是的中点,则的长为( )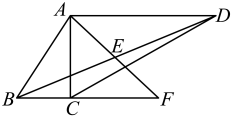 A、 B、 C、2 D、312. 如图,有一种动画程序,屏幕上正方形是黑色区域(含正方形边界),其中 , , , , 用信号枪沿直线发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的的取值范围为( )
A、 B、 C、2 D、312. 如图,有一种动画程序,屏幕上正方形是黑色区域(含正方形边界),其中 , , , , 用信号枪沿直线发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的的取值范围为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 不等式组的解为.14. 2018年春节期间,反季游成为出境游的热门,中国游客青睐的目的地仍主要集中在温暖的东南亚地区.据调查发现2018年春节期间出境游约有700万人,游客目的地分布情况的扇形图如图所示,从中可知出境游东南亚地区的游客约有万人.
 15. 如图,DE为△ABC的中位线,点F在DE上,且∠AFC为直角,若DF=2cm.BC=16cm,则AC的长为cm.
15. 如图,DE为△ABC的中位线,点F在DE上,且∠AFC为直角,若DF=2cm.BC=16cm,则AC的长为cm.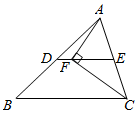 16. 在一列数 , , , , 中,已知 , , , , , ,则 .
16. 在一列数 , , , , 中,已知 , , , , , ,则 .三、解答题
-
17. 已知分式方程 , 由于印刷问题,有一个数“▲”看不清楚.(1)、若“▲”表示的数为6,求分式方程的解;(2)、小华说“我看到答案是原分式方程无解”,请你求出原分式方程中“▲”代表的数.18. 如图,△ABC三个顶点的坐标分别为A(4,5)、B(1,0)、C(4,0).
(1)画出△ABC关于y轴的对称图形△A1B1C1 , 并写出A1点的坐标;
(2)在y轴上求作一点P,使△PAB的周长最小,并求出点P的坐标及△PAB的周长最小值.
 19. 某校为丰富同学们的课余生活,全面提高科学素养,提升思维能力和科投能力,开展了“最强大脑”谢请赛,现从七、八年级中各随机抽取了20名学生的初赛成绩(初春成绩均为整数,满分为分)统计、根理如下:
19. 某校为丰富同学们的课余生活,全面提高科学素养,提升思维能力和科投能力,开展了“最强大脑”谢请赛,现从七、八年级中各随机抽取了20名学生的初赛成绩(初春成绩均为整数,满分为分)统计、根理如下:
七年级抽取学生的初赛成绩: , , , , , , , , , , , , , , , , , , , .七、八年级抽取的学生的初赛成绩统计表:
年级
七年级
八年级
平均数
中位数
众数
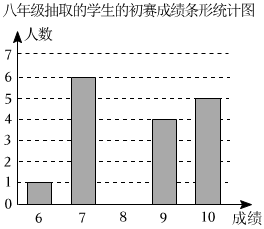 (1)、 , ;(2)、通过计算补全条形统计图;(3)、若该校八年级有名学生参加初赛,规定满分才可进入复赛,请估计八年级进入复赛?20. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地两人之间的距离米与时间分钟之间的函数关系如图所示.
(1)、 , ;(2)、通过计算补全条形统计图;(3)、若该校八年级有名学生参加初赛,规定满分才可进入复赛,请估计八年级进入复赛?20. 学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地两人之间的距离米与时间分钟之间的函数关系如图所示. (1)、根据图象信息,当 分钟时甲乙两人相遇,甲的速度为 米分钟;(2)、求出线段所表示的函数表达式.(3)、当为何值时,甲、乙两人相距米?21. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面的距离AC为2.4m.
(1)、根据图象信息,当 分钟时甲乙两人相遇,甲的速度为 米分钟;(2)、求出线段所表示的函数表达式.(3)、当为何值时,甲、乙两人相距米?21. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面的距离AC为2.4m.
若梯子底端位置保持不动,将梯子斜靠在右墙时,梯子顶端距离地面的距离为1.5m,求小巷有多宽?
22. 如图1将一张矩形纸片沿着对角线向上折叠,顶点C落到点E处,交于点F . (1)、求证:三角形BDF是等腰三角形;(2)、如图2,过点D作 , 交于点G , 连接交于点O . 判断四边形的形状,并说明理由.23. △ABC三个顶点的坐标分别为A(﹣2,1),B(1,2),C(0,3).
(1)、求证:三角形BDF是等腰三角形;(2)、如图2,过点D作 , 交于点G , 连接交于点O . 判断四边形的形状,并说明理由.23. △ABC三个顶点的坐标分别为A(﹣2,1),B(1,2),C(0,3).(1)请画出△ABC,并画出它向右平移3个单位长度后得到的△A1B1C1;
(2)在x轴上求作一点P,使△PAB的周长最小,请画出△PAB,并写出点P的坐标.
 24. 如图,直线与x轴交于点A , 与y轴交于点B , 点P是线段AB的中点.
24. 如图,直线与x轴交于点A , 与y轴交于点B , 点P是线段AB的中点. (1)、在平面内是否存在点 , 使得的值最小?(请填写“是”或“否”);(2)、如果存在满足(1)中条件的点Q , 请直接写出m的值和的最小值;如果不存在,请说明理由.25. 我们定义:如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,形象的可以看作两双手,所以通常称为“手拉手模型”.例如,如图(1),与都是等腰三角形,其中 , 则(SAS).
(1)、在平面内是否存在点 , 使得的值最小?(请填写“是”或“否”);(2)、如果存在满足(1)中条件的点Q , 请直接写出m的值和的最小值;如果不存在,请说明理由.25. 我们定义:如果两个等腰三角形的顶角相等,且顶角的顶点互相重合,则称此图形为“手拉手全等模型”.因为顶点相连的四条边,形象的可以看作两双手,所以通常称为“手拉手模型”.例如,如图(1),与都是等腰三角形,其中 , 则(SAS). (1)、熟悉模型:如(2),已知与都是等腰三角形, , , 且 , 求证:;(2)、运用模型:如(3),P为等边内一点,且 , 求的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以为边构造等边 , 这样就有两个等边三角形共顶点B , 然后连结 , 通过转化的思想求出了的度数;(3)、深化模型:如(4),在四边形中, , , , 求的长.
(1)、熟悉模型:如(2),已知与都是等腰三角形, , , 且 , 求证:;(2)、运用模型:如(3),P为等边内一点,且 , 求的度数.小明在解决此问题时,根据前面的“手拉手全等模型”,以为边构造等边 , 这样就有两个等边三角形共顶点B , 然后连结 , 通过转化的思想求出了的度数;(3)、深化模型:如(4),在四边形中, , , , 求的长.