初中数学同步训练必刷培优卷(北师大版七年级下册 5.2探索轴对称的性质)
试卷更新日期:2024-06-04 类型:同步测试
一、选择题
-
1. 将矩形纸带按如图所示方式折叠,若 , 则( )
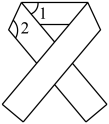 A、130° B、125° C、120° D、115°2. 如图,中, , , 是的中线,点、点分别为线段、上的动点,连接、 , 则的最小值为( )
A、130° B、125° C、120° D、115°2. 如图,中, , , 是的中线,点、点分别为线段、上的动点,连接、 , 则的最小值为( ) A、 B、 C、5 D、63. 如图1,将一条对边互相平行的围巾折叠,并将其抽象成相应的数学模型如图2, , 折痕分别为 , , 若 , , 则等于( )
A、 B、 C、5 D、63. 如图1,将一条对边互相平行的围巾折叠,并将其抽象成相应的数学模型如图2, , 折痕分别为 , , 若 , , 则等于( ) A、 B、 C、 D、4. 如图(1)是长方形纸片, ,将纸片沿AC折叠成图(2),再沿EC折叠成图(3),则图(3)中 为( )
A、 B、 C、 D、4. 如图(1)是长方形纸片, ,将纸片沿AC折叠成图(2),再沿EC折叠成图(3),则图(3)中 为( ) A、 B、 C、 D、5. 如图,在锐角三角形ABC中,AC=6,△ABC的面积为15,∠BAC的平分线交BC与点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
A、 B、 C、 D、5. 如图,在锐角三角形ABC中,AC=6,△ABC的面积为15,∠BAC的平分线交BC与点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ) A、4 B、5 C、6 D、76. 如图,在△ABC中,∠ABC=90°,∠A=30°,BC=1.M、N分别是AB、AC上的任意一点,求MN+NB的最小值为( )
A、4 B、5 C、6 D、76. 如图,在△ABC中,∠ABC=90°,∠A=30°,BC=1.M、N分别是AB、AC上的任意一点,求MN+NB的最小值为( ) A、1.5 B、2 C、 + D、7. 如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( )
A、1.5 B、2 C、 + D、7. 如图,已知点D是等边三角形ABC中BC的中点,BC=2,点E是AC边上的动点,则BE+ED的和最小值为( ) A、 B、 C、3 D、8. △ABC中,∠BAC=60°,AD⊥BC于D,且AD= ,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( )
A、 B、 C、3 D、8. △ABC中,∠BAC=60°,AD⊥BC于D,且AD= ,E、F、G分别为边BC、CA、AB上的点,则△EFG周长的最小值为( ) A、 B、2 C、3 D、39. 如图,在锐角三角形ABC中AB= ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
A、 B、2 C、3 D、39. 如图,在锐角三角形ABC中AB= ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( ) A、4 B、5 C、6 D、210.
A、4 B、5 C、6 D、210.学习了“平行线”后,张明想出了过已知直线外一点画这条直线的平行线的新方法,他是通过折一张半透明的纸得到的(如图①~④):

从图中可知,张明画平行线的依据有( )
(1)两直线平行,同位角相等; (2)两直线平行,内错角相等;
(3)同位角相等,两直线平行; (4)内错角相等,两直线平行.A、(1)(2) B、(2)(3) C、(1)(4) D、(3)(4)二、填空题
-
11. 如图1是一张长方形纸带,∠DEF=20°,若将纸带沿EF折叠成图2,再沿BF折叠成图3,则图3中的∠CFE的度数为°.
 12. 如图,把一张长方形纸片ABCD沿AF折叠,已知∠DBC=20°,当∠BAF=度时,才能使AB'∥BD.
12. 如图,把一张长方形纸片ABCD沿AF折叠,已知∠DBC=20°,当∠BAF=度时,才能使AB'∥BD.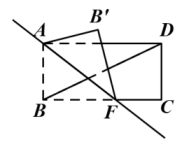 13. 如图,在四边形中, , 在边上分别找一点E、F,使周长最小,此时 .
13. 如图,在四边形中, , 在边上分别找一点E、F,使周长最小,此时 . 14. 如图,在锐角中, , , 的平分线交于点D,点M,N分别是和上的动点,则的最小值是 .
14. 如图,在锐角中, , , 的平分线交于点D,点M,N分别是和上的动点,则的最小值是 .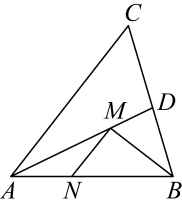 15. 如图,在三角形ABC中,∠A=56°,∠C=46°,D是线段AC上的一个动点,连接BD,把三角形BCD沿BD折叠,点C落在同一平面内的点C'处,当C′D平行于三角形ABC的边时,∠CDB的大小为 .
15. 如图,在三角形ABC中,∠A=56°,∠C=46°,D是线段AC上的一个动点,连接BD,把三角形BCD沿BD折叠,点C落在同一平面内的点C'处,当C′D平行于三角形ABC的边时,∠CDB的大小为 .
三、作图题
-
16. 如图是由小正方形组成的网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.三角形中任意一点经过平移变换后对应点 , 将三角形作同样的平移变换得到三角形 . (点、、的对应点分别是点、、)
 (1)、画出平移后的三角形;(2)、连接 , , 则;(3)、为轴上一动点,当最小时,画出点并直接写点的坐标 ▲ .
(1)、画出平移后的三角形;(2)、连接 , , 则;(3)、为轴上一动点,当最小时,画出点并直接写点的坐标 ▲ .四、解答题
-
17. 在中, , , 过点作使点 , , 按顺时针的顺序排列 , 过点作直线直线 , 垂足为点 , 直线交直线于点 , 连接 .
 (1)、如图 , 若 , 的边都在的内部,作点关于的对称点 .
(1)、如图 , 若 , 的边都在的内部,作点关于的对称点 .▲ , ▲ ;填“”“”或“”
求证: .
(2)、如图 , 若 , 的边都在的外部,当 , , 的面积为时,请直接写出的长;(3)、若 , 有一条边在的内部,请直接写出线段 , , 之间的等量关系.五、实践探究题
-
18.(1)、【初步感知】
如图1,已知△ABC为等边三角形,点D为边BC上一动点(点D不与点B,点C重合).以AD为边向右侧作等边△ADE,连接CE.

求证:
(2)、【类比探究】如图2,若点D在边BC的延长线上,随着动点D的运动位置不同,猜想并证明:①AB与CE的位置关系为: ▲ ;②线段EC、AC、CD之间的数量关系为: ▲ .
 (3)、【拓展应用】
(3)、【拓展应用】如图3,在等边△ABC中,AB=3,点P是边AC上一定点且AP=1,若点D为射线BC上动点,以DP为边向右侧作等边DPE,连接CE、BE.
请问:PE+BE是否有最小值?若有,请直接写出其最小值:若没有,请说明理由.
 19. 问题解决:
19. 问题解决: (1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.
(1)、问题情境:如图1所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到P的距离之和最短?请画出点P的位置;(2)、问题理解:如图2,在△ABC中,AB=AC,AD平分∠BAC,点E是AC边的中点,点P是线段AD上的动点,画出PC+PE取得最小值时点P的位置;(3)、问题运用:如图3,在△ABC中,AB=AC=13,BC=10,AD=12,AD是∠BAC的平分线,当点E、P分别是AC和AD上的动点时,求PC+PE的最小值.
-
-