贵州省2023-2024学年八年级下学期数学期末考试仿真试卷（五）

试卷更新日期：2024-06-04 类型：期末考试

进入出卷网下载

一、选择题

1. 式子 $\sqrt{x + 2}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x > - 3$ B、 $x ≥ - 2$ C、 $x < - 3$ D、 $x ≤ - 2$

查看试题解析
2. 直线 $y = - x + 3$ 与x轴的交点坐标是（）

A、 $(0 ， 3)$ B、 $(0 ， - 3)$ C、 $(3 ， 0)$ D、 $(- 3 ， 0)$

查看试题解析
3. 在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：
成绩/m
1.50
1.60
1.65
1.70
1.75
1.80
人数
2
3
2
3
4
1
则这些运动员成绩的中位数、众数分别为（）

A、1.65、1.70 B、1.65、1.75 C、1.70、1.75 D、1.70、1.70

查看试题解析
4. 已知一次函数表达式为： $y = 4 x - 3$ ，则此一次函数图象不经过第（）象限．

A、一 B、二 C、三 D、四

查看试题解析
5. 下列性质中正方形具有而矩形没有的（）

A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、四个角都是直角

查看试题解析
6. 如图，小明欲控制遥控轮船匀速垂直横渡一条河，但由于水流的影响，实际上岸地点C与欲到达地点B相距10米，结果轮船在水中实际航行的路程 $A C$ 比河的宽度 $A B$ 多2米，则河的宽度 $A B$ 是（）

A、8米 B、12米 C、16米 D、24米

查看试题解析
7. 古秤是一种人类智慧的产物，也是华夏文明的瑰宝之一．如图，我们可以用秤砣到秤纽（秤杆上手提的部分）的水平距离得出秤钩上所挂物体的重量，称重时，若秤钩所挂物重为x斤，秤砣到秤纽的水平距离为ycm．下表为若干次称重时所记录的一些数据：
x（斤）
1
2
3
4
5
6
y（cm）
0.75
1
1.25
1.5
1.75
2
在不超重的情况下，当x=9时，对应的水平距离y为（）

A、2.5 B、2.75 C、2.55 D、2.25

查看试题解析
8. 实数 $a$ 和 $b$ 在数轴上如图所示，化简 $\sqrt{(a + b)^{2}} - \sqrt{(a - 1)^{2}}$ 的结果是（）

A、 $1 - b$ B、 $b - 1$ C、 $b + 1$ D、 $- b - 1$

查看试题解析
9. 如图，EF过平行四边形ABCD对角线的交点O，交AD于点E，交BC于点F，若平行四边形ABCD的周长为36，OE＝3，则四边形EFCD的周长为（　　）

A、28 B、26 C、24 D、20

查看试题解析
10. 如图，以 $O A$ 为直角边作等腰直角三角形 $O A B_{1}$ ，再以 $O B_{1}$ 为直角边在 $△ O A B_{1}$ 外侧作等腰直角三角形 $O B_{1} B_{2}$ ， …，如此继续，得到 $n (n \geq 2)$ 个等腰直角三角形，若图中 $△ O A B_{1}$ 的面积是1，则 $△ O B_{n - 1} B_{n}$ 的面积是（）

A、 $2^{n - 1}$ B、 $2^{n}$ C、 ${(\sqrt{2})}^{n - 1}$ D、 ${(\sqrt{2})}^{n}$

查看试题解析

二、填空题

11. 已知甲、乙两名射击手的10次测试的平均成绩都是8环，方差分别是 $S_{甲}^{2} = 0.4$ （环²）， $S_{乙}^{2} = 3.2$ （环²），则成绩比较稳定的射击手是．

查看试题解析
12. 如图，菱形 $A B C D$ 的对角线 $A C$ ， $B D$ 相交于点O ，且 $A B = 10$ ， $O B = 6$ ，则菱形 $A B C D$ 的面积是.

查看试题解析
13. 我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成.如图，直角三角形的直角边长为a，b，斜边长为c，若b-a=4，c=20，则每个直角三角形的面积为.

查看试题解析
14. 如图，一次函数 $y = k x + b (k \neq 0)$ 的图象为直线 $l_{1}$ ，经过 $A (0 ， 5)$ 和 $D (5 ， 0)$ 两点；一次函数 $y = x + 1$ 的图象为直线 $l_{2}$ ，与x轴交于点 $C$ ，两直线 $l_{1}$ ， $l_{2}$ 相交于点B．则关于 $x$ 的不等式 $0 < k x + b \leq x + 1$ 的解集是．

查看试题解析

三、解答题

15. 为了改进几何教学，张老师选择A，B两班进行教学实验研究，在实验班 $B$ 实施新的教学方法，在控制班 $A$ 采用原来的教学方法.在实验开始前，进行一次几何能力测试(前测，总分25分)，经过一段时间的教学后，再用难度、题型、总分相同的试卷进行测试(后测，总分25分)，得到前测和后测的数据并整理成表和表2.
表1：前测数据
测试分数 $x$
$0 < x$ $⩽ 5$
$5 < x$ $⩽ 10$
$10 < x$ $⩽ 15$
$15 < x$ $⩽ 20$
$20 < x$ $⩽ 25$
控制班A
28
9
9
3
1
实验班B
25
10
8
2
1
表2：后测数据
测试分数 $x$
$0 < x$ $⩽ 5$
$5 < x$ $⩽ 10$
$10 < x$ $⩽ 15$
$15 < x$ $⩽ 20$
$20 < x$ $⩽ 25$
控制班A
14
16
12
6
2
实验班B
6
8
11
18
3

(1)、A，B两班的学生人数分别是多少?

(2)、请选择一种适当的统计量，分析比较 $A$ ， $B$ 两班的后测数据.

(3)、通过分析前测、后测数据，请对张老师的教学实验效果进行评价.

查看试题解析
16. 如图，在正方形网格中，每个小正方形网格的边长均为1，点A ， B ， C ， D均在格点上．

(1)、判断 $△ A C D$ 的形状，并说明理由；

(2)、求四边形 $A B C D$ 的面积．

查看试题解析
17. 在“看图说故事”活动中，某学习小组结合图象设计了一个问题情境．
已知小明家、社区阅览室、博物馆依次在同一条直线上，社区阅览室离小明家 $1 k m$ ，博物馆离小明家 $3 k m$ ，小明从家出发，匀速步行了 $10 m i n$ 到社区阅览室；在阅览室停留 $30 m i n$ 后，匀速步行了 $25 m i n$ 到博物馆；在博物馆停留 $60 m i n$ 后，匀速骑行了 $15 m i n$ 返回家，给出的图象反映了这个过程中小明离家的距离 $y k m$ 与离开家的时间 $x m i n$ 之间的对应关系．

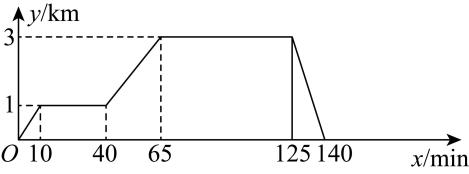
请根据相关信息，解答下列问题：

(1)、填表：
离开家的时间/min
5
8
20
50
120
离家的距离/km
0.5
1.8

(2)、填空：
①社区阅览室到博物馆的距离为 $k m$ ；
②小明从博物馆返回家的速度为 $k m / m i n$ ．

(3)、当 $10 \leq x \leq 125$ 时，请直接写出y关于x的函数解析式．

查看试题解析
18. 如图，有一架秋千，当它静止时，踏板离地的垂直高度DE＝1m，将它往前推送4m（水平距离BC＝4m）时，秋千的踏板离地的垂直高度BF＝2m，秋千的绳索始终拉得很直，求绳索AD的长度．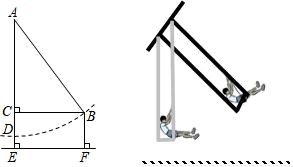

查看试题解析
19. 如图，在平行四边形ABCD中，E，F是直线BD上的两点，DE=BF．

(1)、求证：四边形AECF是平行四边形；

(2)、若AD⊥BD，AB=5，BC=3，且EF－AF=2，求DE的长．

查看试题解析
20. 在计算 $2 \sqrt{6} \times \sqrt{3} - \sqrt{24} \div \sqrt{3}$ 的值时，小亮的解题过理如下：
$\begin{array}{r} 解：2 \sqrt{6} \times \sqrt{3} - \sqrt{24} \div \sqrt{3} \\ = 2 \sqrt{6 \times 3} - \sqrt{\frac{24}{3}} \dots \dots (1) \\ = 2 \sqrt{18} - \sqrt{8} \dots \dots (2) \\ = (2 - 1) \sqrt{18 - 8} \dots \dots (3) \\ = \sqrt{10} ， \dots \dots (4) \end{array}$

(1)、老师认为小亮的解法有错，请你指出小亮是从步骤(填序号)开始出错的.

(2)、请你给出正确的解题过程.

查看试题解析
21. 在平面直角坐标系 $x O y$ 中，将经过点 $A (- 1, 2)$ 的直线 $l_{1} : y = 2 x + b$ 向下平移5个单位得直线 $l_{2}$ ，直线 $l_{2}$ 经过点 $B (1, m)$ ，

(1)、求直线 $l_{2}$ 的解析式及点 $B$ 的坐标；

(2)、直线 $l_{2}$ 与 $y$ 轴交于点 $C$ ，求 $△ A B C$ 的面积；

查看试题解析
22. 几何与探究

(1)、【初步感知】如图1，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 16$ ，将 $∠ A$ 沿 $D E$ 折叠，使点A与点B重合，折痕和 $A C$ 交于点E ， $E C = 6$ ，求 $B C$ 的长；

(2)、【深入探究】如图2，将矩形 $A B C D$ 沿着对角线 $B D$ 折叠，使点C落在 $C^{'}$ 处， $B C^{'}$ 交 $A D$ 于E ，若 $A B = 10$ ， $B C = 16$ ，求 $A E$ 的长；

(3)、【拓展延伸】如图3，在矩形 $A B C D$ 中， $A B = 10$ ， $B C = 16$ ，点E为射线 $A D$ 上一个动点，把 $△ A B E$ 沿直线 $B E$ 折叠，当点A的对应点F刚好落在线段 $B C$ 的垂直平分线上时，求 $A E$ 的长．

查看试题解析

测试分数 $x$	$0 < x$ $⩽ 5$	$5 < x$ $⩽ 10$	$10 < x$ $⩽ 15$	$15 < x$ $⩽ 20$	$20 < x$ $⩽ 25$
控制班A	28	9	9	3	1
实验班B	25	10	8	2	1

成绩/m	1.50	1.60	1.65	1.70	1.75	1.80
人数	2	3	2	3	4	1

x（斤）	1	2	3	4	5	6
y（cm）	0.75	1	1.25	1.5	1.75	2

离开家的时间/min	5	8	20	50	120
离家的距离/km	0.5			1.8