贵州省2023-2024学年八年级下学期数学期末考试仿真试卷（四）

试卷更新日期：2024-06-04 类型：期末考试

进入出卷网下载

一、选择题

1. 9的算术平方根是（）

A、 $\pm 3$ B、 $\pm \sqrt{9}$ C、3 D、-3

查看试题解析
2. 甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数都是9环，方差分别是 $S_{甲}^{2} = 0.61 ， S_{乙}^{2} = 0.52 ，$ $S_{丙}^{2} = 0.53 ， S_{丁}^{2} = 0.42$ ，则射击成绩比较稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
3. 如图，为测量位于一水塘旁的两点A，B间的距离，在地面上确定点O，分别取OA，OB的中点C，D，量得CD＝10m，则A，B之间的距离是（）

A、5m B、10m C、20m D、40m

查看试题解析
4. 一次函数 $y = x + 1$ 的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 如图，在数轴上点 $A^{'}$ 表示的实数是（）

A、 $- \sqrt{5}$ B、 $- \sqrt{3}$ C、－2 D、 $\sqrt{5}$

查看试题解析
6. 下列说法正确的是（）

A、菱形的四个内角都是直角 B、正方形的每一条对角线平分一组对角 C、矩形的对角线互相垂直 D、平行四边形是轴对称图形

查看试题解析
7. 如图所示，长方形纸片ABCD中，AB＝5cm ， BC＝10cm ，现将其沿EF对折，使得点C与点A重合，则AF长（）

A、3cm B、 $2 \sqrt{5}$ cm C、5cm D、 $\frac{25}{4}$ cm

查看试题解析
8. 如图，在平面直角坐标系中，矩形 $O A B C$ 的点 $A$ 和点 $C$ 分别落在 $y$ 轴和 $x$ 轴正半轴上， $O C = 8$ ，直线 $l ： y = 2 x + 6$ 经过点 $A$ ，将直线 $l$ 向下平移 $m$ 个单位，若直线可将矩形 $O A B C$ 的面积平分，则 $m$ 的值为（）

A、11 B、9 C、6 D、5

查看试题解析

二、填空题

9. 使代数式 $\sqrt{x - 1}$ 有意义的x取值范围是．

查看试题解析
10. 某校在期末考核学生的体育成绩时，将早锻炼及体育课外活动表现占成绩的20%，体育理论测试占30%，体育技能测试占50%．小颖的上述成绩分别为92分、80分、84分，则小颖这学期的体育成绩是分

查看试题解析
11. 小明从家跑步到学校，到达学校后马上沿原路步行回家，如图所示为小明离家的路程 $y (m)$ 与时间 $t (m i n)$ 之间的函数图象，则小明回家的速度是每分钟步行m．

查看试题解析
12. 如图，在平行四边形 $A B C D$ 中， $∠ A B C = 120 °$ ， $A B = \sqrt{5}$ ，连接 $B D$ ，且 $B D ⊥ C D$ ， $C E$ 平分 $∠ D C B$ 交 $A D$ 与于点 $E$ ．点 $N$ 在 $B C$ 边上， $B C = 4 C N$ ，若线段 $P Q$ （点 $P$ 在点 $Q$ 的左侧）在线段 $C E$ 上运动， $P Q = \frac{\sqrt{15}}{2}$ ，连接 $B P$ ， $N Q$ ，则 $B P + P Q + Q N$ 的最小值为．

查看试题解析

三、计算题

四、解答题

13. 如图，在△ABC中，AB＝4，AC＝3，BC＝5，DE是BC的垂直平分线，交BC于D ， AB于E.

(1)、求证：△ABC为直角三角形；

(2)、求AE的长．

查看试题解析
14. 如图，已知 $△ A B C$ ， $∠ C = 50 °$ ，将 $A B$ 沿射线 $B C$ 的方向平移至 $A' B'$ ，使 $B'$ 为 $B C$ 的中点，连结 $A A'$ ，记 $A' B'$ 与 $A C$ 的交点为 $O$ ．

(1)、求证： $△ A O A'$ ≌ $△ C O B'$ ；

(2)、若 $A C$ 平分 $∠ B A A'$ ，求 $∠ B$ 的度数．

查看试题解析
15. 2023年10月8日第十九届亚运会在中国杭州圆满闭幕．某校举行了七、八年级亚运知识竞赛，现分别在两个年级中各随机抽取10名学生，统计这部分学生的竞赛成绩，并对数据进行收集、整理和分析（其中成绩大于等于80的视为优秀）：
【收频数据】
七年级10名同学测试成绩统计如下：84，78，85，75，72，91，79，72，69，95
八年级10名同学测试成绩统计如下：85，80，76，84，80，72，92，74，75，82
【整理、分析数据】两组数据的平均数、中位数、众数、优秀率如表：

平均数
中位数
众数
优秀率
七年级
80
a
72
$40 %$
八年级
80
80
b
$c %$
【问题解决】根据以上信息，解答下列问题：

(1)、填空： $a =$ ， $b =$ ， $c =$ ；

(2)、根据以上数据，你认为该校七、八年级中哪个年级学生知识竞赛成绩更好？请说明理由．

(3)、若该校七年级学生共1000人，八年级学生共1200人，请估计这两个年级竞赛成绩达到优秀的学生的总人数．

查看试题解析
16. 如图，在平面直角坐标系中，一次函数 $y = k x + b$ 的图象经过点 $A (- 2 ， 6)$ ，且与x轴相交于点B，与正比例函数 $y = 3 x$ 的图象相交于点C，点C的横坐标为1.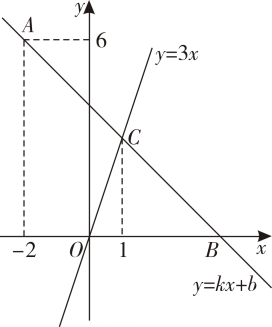

(1)、求k、b的值；

(2)、请直接写出不等式 $k x + b > 3 x$ 的解集；

(3)、若点D在y轴上，且满足 $S_{△ D O C} = S_{△ B O C}$ ，求点D的坐标.

查看试题解析
17. 如图，某小区内有一块四边形空地 $A B C D$ ，计划将这块空地建成一个花园，以美化居住环境.经测量得知， $∠ B = 90 °$ ， $A B = 8$ 米， $B C = 6$ 米， $C D = 26$ 米， $A D = 24$ 米.

(1)、求这块四边形空地的面积；

(2)、预计花园每平方米造价为200元，该小区修建这个花园需要花费多少元?

查看试题解析
18. 如图，在四边形ABCD中， $A B / / D C$ ， $A B = A D$ ，对角线AC ， BD相交于点O ， O是BD的中点，过点C作 $C E / / D B$ 交AB的延长线于点E ，连接OE ．

(1)、求证：四边形ABCD是菱形；

(2)、若 $∠ D A B = 60 °$ ，且 $A B = 6$ ，求OE的长．

查看试题解析
19.

(1)、【问题背景】如图1，点E、F分别在正方形 $A B C D$ 的边 $B C$ 、 $C D$ 上， $∠ E A F = 45 °$ ，连接 $E F$ ，则有 $E F = B E + D F$ ，试说明理由；

(2)、【迁移应用】如图2，四边形 $A B C D$ 中， $A B = A D$ ， $∠ B A D = 90 °$ ，点E、F分别在边 $B C$ 、 $C D$ 上， $∠ E A F = 45 °$ ，若 $∠ B$ ， $∠ D$ 都不是直角，且 $∠ B + ∠ D = 180 °$ ，试探究 $E F$ 、 $B E$ 、 $D F$ 之间的数量关系；

(3)、【联系拓展】如图3，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，点D、E均在边 $B C$ 上，且 $∠ D A E = 45 °$ ，猜想 $B D$ 、 $D E$ 、 $E C$ 满足的等量关系．（直接写出结论，不需要证明）．

查看试题解析

	平均数	中位数	众数	优秀率
七年级	80	a	72	$40 %$
八年级	80	80	b	$c %$