初中数学同步训练必刷基础卷（北师大版七年级下册6.2频率的稳定性）

试卷更新日期：2024-06-04 类型：同步测试

进入出卷网下载

一、选择题

1. 从某郁金香种子中抽取7批，在同一条件下进行发芽试验，有关数据如下表：
种子粒数
100
300
500
700
1000
2000
3000
发芽种子粒数
80
239
403
559
802
1594
2403
发芽频率
$\begin{array}{l} 0.800 \end{array}$
$\begin{array}{l} 0.797 \end{array}$
$\begin{array}{l} 0.806 \end{array}$
$\begin{array}{l} 0.799 \end{array}$
$\begin{array}{l} 0.802 \end{array}$
$\begin{array}{l} 0.797 \end{array}$
$\begin{array}{l} 0.801 \end{array}$
根据以上数据，该郁金香种子发芽的概率约为（）

A、 $0.70$ B、 $0.75$ C、 $0.80$ D、 $0.85$

查看试题解析
2. 一个不透明的口袋里装有除颜色外都相同的10个白球和若干个红球，在不允许将球倒出来数的前提下，小红为了估计其中的红球数，采用如下方法：先将口袋中的球摇匀，再从口袋里随机摸出一球，记下颜色，然后把它放回口袋中，不断重复上述过程，小红共摸了1000次，其中有202次摸到白球，因此小红估计口袋中的红球有（）

A、60个 B、50个 C、40个 D、30个

查看试题解析

3. 王师傅对某批零件的质量进行了随机抽查，并将抽查结果绘制成如下表格，请你根据表格估计，若从该批零件中任取一个，为合格零件的概率为（）

随机抽取的零件个数 $n$	20	50	100	500	1000
合格的零件个数 $m$	18	46	91	450	900
零件的合格率 $\frac{m}{n}$	0.9	0.92	0.91	0.9	0.9

A、0.9 B、0.8 C、0.5 D、0.1

查看试题解析

4. 某一超市在“五•一”期间开展有奖促销活动，每买100元商品可参加抽奖一次，中奖的概率为 $\frac{1}{3}$ ．小张这期间在该超市买商品获得了三次抽奖机会，则小张（）

A、能中奖一次 B、能中奖两次 C、至少能中奖一次 D、中奖次数不能确定

查看试题解析

5. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如下的表格，

实验次数	100	200	300	500	800	1000	2000
频率	0.365	0.328	0.330	0.334	0.336	0.332	0.333

则符合这一结果的实验最有可能的是（）

A、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是梅花 B、抛一枚硬币，出现反面的概率 C、袋子里有除了颜色都一样3个红球，2个白球,随机摸一个球是白球的概率 D、抛一个质地均匀的正六面体骰子，向上的面点数大于4

查看试题解析

6. 用频率估计概率，可以发现，抛掷硬币，“正面朝上”的概率为0.5，那么掷一枚质地均匀的硬币10次，下列说法正确的是（）

A、每两次必有1次正面向上 B、可能有5次正面向上 C、必有5次正面向上 D、不可能有10次正面向上

查看试题解析
7. 某林业部门要考察某种幼树在一定条件下的移植成活率，下图是这种幼树在移植过程中成活情况的一组数据统计结果.下面三个推断：①当移植棵数是1500时，该幼树移植成活的棵数是1356，所以“移植成活”的概率是0.904；②随着移植棵数的增加，“移植成活”的频率总在0.880附近摆动，显示出一定的稳定性，可以估计这种幼树“移植成活”的概率是0.880；③若这种幼树“移植成活”的频率的平均值是0.875，则“移植成活”的概率是0.875.其中合理的是（）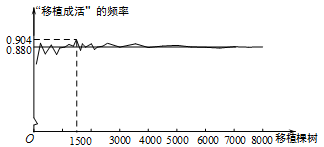

A、①③ B、②③ C、① D、②

查看试题解析
8. 某位篮球爱好者进行了三轮投篮试验，结果如下表：
轮数
投球数
命中数
命中率
第一轮
10
8
0.8
第二轮
15
10
0.67
第三轮
12
9
0.75
则他的投篮命中率为（）

A、 $\frac{4}{5}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、不能确定

查看试题解析
9. 下列四种说法；①为了了解某批灯泡的使用寿命可以用普查的方式；②“在同一年出生的367名学生中，至少有两人的生日是同一天”是必然事件；③“打开电视机，正在播放少儿节目”是随机事件；④如果一个事件发生的概率只有十亿分之一，那么它是不可能事件．其中，正确的说法是( )

A、②④ B、①② C、③④ D、②③

查看试题解析

二、填空题

10. 在一个不透明的袋中装有除颜色外完全相同的a个小球，其中红球的个数为2，随机摸出一个球记下颜色后再放回袋中，通过大量重复实验发现，摸到红球的频率稳定于0.1附近，那么可以推算出a的值大约是．

查看试题解析

11. 某冰壶运动队的队员们要反复训练在无阻碍的情况下，将冰壶准确投掷到中心区域，现将其平时训练的结果统计如下：

投掷次数	20	40	100	200	400	1000
投掷到中心区域的频数	15	34	88	184	356	910
投掷到中心区域的频率	0.75	0.85	0.88	0.92	0.89	0.91

估计这支运动队在无阻碍情况下将冰壶投掷到中心区域的概率为．（结果精确到0.1）

查看试题解析

12. 绿化公司对某种花苗移植的成活率进行调查，结果如表所示：

移植总数（n）	400	750	1500	3500	7000	9000	10000
成活数（m）	369	662	1335	3203	6335	8073	9013
成活的频率 $\frac{m}{n}$	0.923	0.883	0.890	0.915	0.905	0.897	0.901

根据表中数据，估计这种花苗移植的成活概率为．（精确到0.1）

查看试题解析

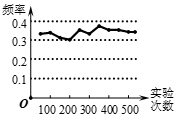
13. 如图是某小组同学做“频率估计概率”的实验时，绘出的某一实验结果出现的频率折线图，则符合图中这一结果的实验可能是（填序号）.
①抛一枚质地均匀的硬币，落地时结果“正面朝上”；

②在“石头，剪刀，布”的游戏中，小明随机出的是剪刀；

③四张一样的卡片，分别标有数字1，2，3，4，从中随机取出一张，数字是1.

查看试题解析

14. 一抹“凉都绿”，一杯生态茶.凉都茶叶因其得天独厚的生长条件，具有早采、富硒、有机的天然品质，凉都具备发展优质茶产业的先天地理优势，茶产业已成为六盘水农业特色产业之一，下表是我市某茶叶种植合作社脱贫攻坚期间茶树种植成活情况统计表：

种植茶树棵树	3000	5000	8000	10000	20000	$\dots$
成活棵树	2690	4507	7195	9003	17998	$\dots$
成活率	0.8967	0.9014	0.8993	0.9003	0.8999	$\dots$

根据这个表格，请估计这个合作社茶树种植成活的概率为（结果保留一位小数）

查看试题解析

15. 有五个面的石块，每个面上分别标记1，2，3，4，5，现随机投掷100次，每个面落在地面上的次数如下表，估计石块标记3的面落在地面上的概率是.

石块的面

1

2

3

4

5

频数

17

28

15

16

24

查看试题解析
16. 在一次抽奖活动中，中奖概率是0.12，则不中奖的概率是．

查看试题解析

三、解答题

17. 甲班56人，其中身高在160厘米以上的男同学10人，身高在160厘米以上的女同学3人，乙班80人，其中身高在160厘米以上的男同学20人，身高在160厘米以上的女同学8人．如果想在两个班的160厘米以上的女生中抽出一个作为旗手，在哪个班成功的机会大？为什么？

查看试题解析

四、综合题

18. 疫情之后，各大商家为吸引顾客，纷纷采用多种促销手段.其中一个商场设立了一个购物满50元，可以获得一次转动转盘的机会，当转盘停止时，指针落在那个区域就可以得到相应的奖品.下表是活动进行中的一组统计数据：

转动转盘的次数	100	200	500	1000	1500	2000
落在“抽纸”的次数 $n$	51	99	251	502	750	1002
落在“抽纸”的频率 $\frac{n}{m}$

(1)、完成上表；

(2)、请估计，当

m

很大时，频率是多少？

(3)、假如你去转动转盘一次，你获得“抽纸”的概率是多少？

查看试题解析

种子粒数	100	300	500	700	1000	2000	3000
发芽种子粒数	80	239	403	559	802	1594	2403
发芽频率	$\begin{array}{l} 0.800 \end{array}$	$\begin{array}{l} 0.797 \end{array}$	$\begin{array}{l} 0.806 \end{array}$	$\begin{array}{l} 0.799 \end{array}$	$\begin{array}{l} 0.802 \end{array}$	$\begin{array}{l} 0.797 \end{array}$	$\begin{array}{l} 0.801 \end{array}$

轮数	投球数	命中数	命中率
第一轮	10	8	0.8
第二轮	15	10	0.67
第三轮	12	9	0.75

石块的面	1	2	3	4	5
频数	17	28	15	16	24