广西壮族自治区北海市合浦县2023-2024学年八年级下学期期中数学试题

试卷更新日期：2024-06-04 类型：期中考试

进入出卷网下载

一、选择题（每小题3分，共36分）

1. 平行四边形都具有的性质是（）

A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、邻边相等

查看试题解析
2. 在直角三角形中，若直角边为6和8，则斜边为（）

A、7 B、8 C、9 D、10

查看试题解析
3. 已知直角三角形30°角所对的直角边长为5，则斜边的长为（）

A、5 B、10 C、8 D、12

查看试题解析
4. 小明要判断一块平行四边形木板是否是矩形，以下测量方法正确的是（）

A、测量两组对边是否相等 B、测量一组邻边是否相等 C、测量对角线是否相等 D、测量对角线是否互相垂直

查看试题解析
5. 一个三角形的三边长分别为9，12，15，则它的面积为（）

A、135 B、90 C、108 D、54

查看试题解析
6. 在四边形ABCD中，AB∥CD且AB=CD，若∠B=56°，则∠C的度数是（）

A、56° B、65° C、114° D、124°

查看试题解析
7. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， DE为AB的垂直平分线， $C D = D E = 2$ ，则 $A B =$ （）

A、4 B、8 C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
8. 矩形具有而菱形不一定具有的性质是（）

A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线相等且互相垂直

查看试题解析
9. 如图，三条公路把A、B、C三个村庄连成一个三角形区域，某地区决定在这个三角形区域内修建一个集贸市场，使集贸市场到三条公路的距离相等，则这个集贸市场应建在（）

A、在AC、BC两边高线的交点处 B、在AC、BC两边中线的交点处 C、在 $∠ A$ 、 $∠ B$ 两内角平分线的交点处 D、在AC、BC两边垂直平分线的交点处

查看试题解析
10. 等腰梯形的上底是2cm，腰长是4cm，一个底角是60°，则等腰梯形的下底是（　　）

A、5cm B、6cm C、7cm D、8cm

查看试题解析
11. 如图，菱形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点O，若 $A C = 16$ ， $B D = 8$ ，则菱形 $A B C D$ 的边长为（）

A、 $4 \sqrt{5}$ B、 $8 \sqrt{5}$ C、8 D、10

查看试题解析
12. 如图，动点P从点A出发，沿着圆柱的侧面移动到BC的中点S ，若 $B C = 6$ ，点P移动的最短距离为5，则圆柱的底面周长为（）

A、4 B、4π C、8 D、10

查看试题解析

二、填空题（每小题2分，共12分）

13. 已知一个多边形的内角和是2340°，则这个多边形的边数是．

查看试题解析
14. 等腰梯形的上底是10cm，下底是16cm，高是4cm，则等腰梯形的周长为cm．

查看试题解析
15. 如图，要测量池塘两岸相对的A，B两点间的距离，可以在池塘外选一点C，连接AC，BC，分别取AC，BC的中点D，E，测得DE＝50m，则AB的长是m.

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， D是 $A C$ 的中点．若 $B D = 8$ ，则 $A D =$ ．

查看试题解析
17. 如图， $▱ A B C D$ 中，AE平分 $∠ B A D$ ，若 $C E = 3$ cm， $A B = 4$ cm，则 $▱ A B C D$ 的周长为．

查看试题解析
18. 如图，把矩形ABCD沿EF翻折，点B恰好落在AD边的B'处，若 $A E = 2$ ， $D E = 6$ ， $∠ E F B = 60 °$ ，则矩形ABCD的面积是．

查看试题解析

三、解答题（共72分，解答应写出文字说明、证明过程或演算步骤）

19. 如图，在 $△ A B C$ 中， $C B ⊥ A B$ ， $∠ B A C = 45 °$ ， F是AB延长线上一点，点E在BC上，且 $A E = C F$ ．求证： $△ A B E ≌ △ C B F$ ．

查看试题解析
20. 如图，在▱ABCD中，AE⊥BC于点E，CF⊥AB于点F，且AE＝CF，求证：▱ABCD是菱形.

查看试题解析
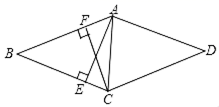21. 一个多边形的每一个内角都相等，且每个外角都等于和它相邻的内角的一半．

(1)、求这个多边形是几边形；

(2)、求这个多边形的内角和．

查看试题解析
22. 如图，已知在梯形ABCD中， $A D ∥ B C$ ， $A D = A B$ ， $B C = 2 A D$ ， E是BC边的中点，AE、BD相交于点F ．

(1)、求证：四边形AECD是平行四边形；

(2)、设边CD的中点为G ，连接EG ．求证：四边形FEGD是矩形．

查看试题解析
23. 如图，在平行四边形 $A B C D$ 中，过点 $D$ 作 $D E ⊥ A B$ 于点 $E ，$ 点 $F$ 在 $C D$ 边上， $C F = A E ，$ 连接AF，BF.

(1)、求证：四边形 $B F D E$ 是矩形；

(2)、若 $A F$ 平分 $∠ D A B ，$ $C F = 3 ， D F = 5 ，$ 求四边形 $B F D E$ 的面积．

查看试题解析
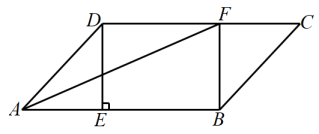24. 如图，长方形ABCD中， $A B = 4$ ， $B C = 3$ ， P为AD上一点，将 $△ A B P$ 沿BP翻折至 $△ E B P$ ， BE与CD相交于点G ， PE与CD相交于点O ，且 $O E = O D$ ．

(1)、求证： $D P = E G$ ；

(2)、求AP的长．

查看试题解析
25. 已知BD垂直平分AC ， $∠ B C D = ∠ A D F$ ， $A F ⊥ A C$ ．

(1)、求证：四边形ABDF是平行四边形；

(2)、若 $A F = 14$ ， $D F = 13$ ， $A D = 15$ ，求AC的长．

查看试题解析
26. 【问题情境】已知在四边形ABCD中，M为边AD上一点（不与点A ， D重合），连接BM ，将 $△ A B M$ 沿BM折叠得到 $△ N B M$ ，点A的对应点为点N ．

(1)、【问题初探】如图（1），若四边形ABCD是正方形，点N落在对角线BD上，连接AN并延长交CD于点G ，写出与 $∠ D G A$ 相等的角：（写出一个即可）：

(2)、【拓展变式】如图（2），若四边形ABCD是矩形，点N恰好落在AB的垂直平分线EF上，EF与BM交于点G ．求证： $△ G M N$ 是等边三角形；

(3)、【问题解决】如图（3），若四边形ABCD是平行四边形， $B C = 2 A B = 4$ ， $∠ A B C = 60 °$ ，点N落在线段BC上，P为AB的中点，连接DP ， PN ， DN ，求 $△ P N D$ 的面积．

查看试题解析