2024年北师大版数学七年级第二学期期末模拟试卷四

试卷更新日期：2024-06-03 类型：期末考试

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列计算正确的是（）

A、 $2 a + 3 b = 5 a b$ B、 $(- a^{3} b^{4})^{2} = a^{6} b^{8}$ C、 $a^{6} \div a^{2} = a^{3}$ D、 $(a + b)^{2} = a^{2} + b^{2}$

查看试题解析
2. 美术老师布置同学们设计窗花，下列作品为轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若 $() \cdot 2 a^{2} b = 2 a^{3} b$ ，则括号内应填的单项式是（）

A、a B、 $2 a$ C、 $a b$ D、 $2 a b$

查看试题解析
4. 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为（）

A、22×10^﹣10 B、2.2×10^﹣10 C、2.2×10^﹣9 D、2.2×10^﹣8

查看试题解析
5. 如图， $A D$ ， $A E$ ， $A F$ 分别是 $△ A B C$ 的中线、角平分线、高线，下列结论中错误的是（）

A、 $C D = \frac{1}{2} B C$ B、 $2 ∠ B A E = ∠ B A C$ C、 $∠ C + ∠ C A F = 90 °$ D、 $A E = A C$

查看试题解析
6. 一副三角板如图摆放，三角板ADF的斜边FD与三角板ABC的直角边AC相交于点 $E$ ，点 $D$ 在直角边BC上，且 $F D / / A B, ∠ B = 3 0^{°}$ ，则 $∠ A D B$ 的度数是（）

A、 $9 5^{°}$ B、 $10 5^{°}$ C、 $11 5^{°}$ D、 $12 5^{°}$

查看试题解析
7. 如图，这是一个平分角的仪器， $A B = A D ， B C = D C$ ，将点A放在一个角的顶点，使AB、AD分别与这个角的两边重合，可证 $△ A D C ≌ △ A B C$ ，从而得到AC就是这个角的平分线．其中证明 $△ A D C ≌ △ A B C$ 的数学依据是（）

A、SSS B、ASA C、SAS D、AAS

查看试题解析
8. 若 $x^{2} - 2 m x + 9$ 是关于 $x$ 的完全平方式，则 $m$ 的值为（）

A、 $\pm 3$ B、 $\pm 6$ C、3 D、6

查看试题解析
9. 七巧板是一种古老的中国传统智力玩具，被誉为“东方魔板”，它是由5个等腰直角三角形、1个正方形和1个平行四边形组成的．如图是由“七巧板”组成的边长为 $5 c m$ 的正方形，若在正方形区域内随意取一点，则该点取到阴影部分的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{7}$ C、 $\frac{1}{8}$ D、 $\frac{2}{7}$

查看试题解析
10. 如图，AD是△ ABC中∠ BAC的角平分线，DE⊥AB于点E，S_△ABC＝7，DE＝2， AB＝4，则AC长是（）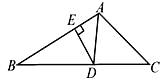

A、3 B、4 C、6 D、5

查看试题解析

二、填空题（每题3分，共18分）

11. 已知x+ $\frac{1}{x}$ =6，则x²+ $\frac{1}{x^{2}}$ =.

查看试题解析
12. 如图，点B、E、C、F在一条直线上，AB∥DE，且AB=DE，请添加一个条件，使△ABC≌△DEF.

查看试题解析
13. 等腰三角形一腰上的高与另一腰的夹角为40°，求底角的度数

查看试题解析
14. 如图 $①$ 是长方形纸带， $∠ C F E = 55 °$ ，将纸带沿 $E F$ 折叠成图 $②$ ，再沿 $G E$ 折叠成图 $③$ ，则图 $③$ 中 $∠ D E F$ 的度数是．

查看试题解析
15. 如图①，一种圆环的外圆直径是8cm，环宽1cm．如图②，若把2个这样的圆环扣在一起并拉紧，则其长度为cm；如图③，若把x个这样的圆环扣在一起并拉紧，其长度为ycm，则y与x之间的关系式是．

查看试题解析

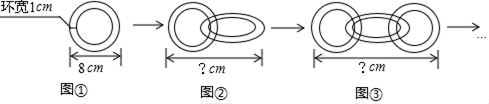
三、解答题（共8题，共72分）

16. 计算：

(1)、 ${(\frac{1}{2})}^{- 1} + {(π - 2024)}^{0} - {(- 1)}^{2024}$ ；

(2)、 $2 a^{2} b (\frac{1}{2} a b - 3 a b^{2})$ ．

查看试题解析
17. 先化简，再求值： $[{(3 x - y)}^{2} - (x + y) (x - y) - 2 y^{2}] \div (- 2 x)$ ，其中 $x = 3$ ， $y = - 1$ .

查看试题解析
18. 如图是一种躺椅及其结构示意图，扶手AB与底座CD都平行于地面EF ，前支架OE与后支架OF分别与CD交于点G和点D ， AB与DM交于点N ， ∠AOE＝∠BNM ．

(1)、请对 $O E ∥ D M$ 说明理由；

(2)、若OE平分∠AOF ， ∠ODC＝30°，求扶手AB与靠背DM的夹角∠ANM的度数．

查看试题解析
19. 下表是某厂质检部门对该厂生产的一批排球质量检测的情况．
抽取的排球数描取格品数
$500$
$1000$
$1500$
$2000$
$3000$
合格品数
$471$
$946$
$1425$
$b$
$2853$
合格品频率
$a$
$0.946$
$0.950$
$0.949$
$0.951$

(1)、求出表中 $a =$ ， $b =$ ．

(2)、从这批排球中任意抽取一个，是合格品的概率约是 $. ($ 精确到 $0.01)$

(3)、如果生产 $25000$ 个排球，那么估计该厂生产的排球合格的有多少个？

查看试题解析
20. 如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE＝DF，∠A＝∠D．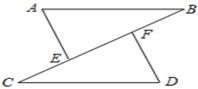

(1)、求证：AB＝CD；

(2)、若AB＝CF，∠B＝40°，求∠D的度数．

查看试题解析

21. 某通讯公司公布了收费标准，其中包月129元时，国内拨打电话超出部分0.15元/分.由于业务多，小明的爸爸打电话已超出了包月费.用x表示国内拨打超出时间，y表示国内拨打超出部分的电话费，下表是超出部分国内拨打的收费标准

超出时间x/分	1	2	3	4	5	……
超出部分的电话费y/元	0.15	0.30	0.45	0.60	0.75	……

(1)、这个表反映了哪两个变量之间的关系？哪个是自变量？哪个是因变量？

(2)、如果国内拨打电话超出6分钟，那么超出部分的电话费是多少元？

(3)、如果某次国内拨打电话超出部分的费用是1.2元，那么小明的爸爸国内拨打电话超出几分钟？

查看试题解析

22. 下面是小东设计的尺规作图过程．
已知：如图，在Rt△ABC中，∠ABC＝90°，
求作：点D ，使点D在BC边上，且到AB和AC的距离相等．
作法：①如图，以点A为圆心，任意长为半径画弧，分别交AB，AC于点M、N；
②分别以点M ， N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P；
③画射线AP ，交BC于点D ．
所以点D即为所求．
根据小东设计的尺规作图过程：

(1)、使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：过点D作DE⊥AC于点E ，连接MP ， NP ．
在△AMP与△ANP中，
∵AM＝AN ， MP＝NP ， AP＝AP ，
∴△AMP≌△ANP（SSS）．
∴∠ ▲ ＝∠ ▲ ．
∵∠ABC＝90°，
∴DB⊥AB ．
又∵DE⊥AC ，
∴DB＝DE（ ▲ ）（填推理的依据）

查看试题解析
23. 如图，在△ABC中，∠ABC的平分线与AC的垂直平分线相交于点D，过点D作DF⊥BC，DG⊥AB，垂足分别为F、G.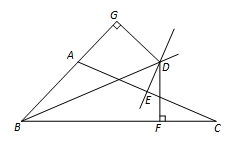

(1)、求证：AG=CF；

(2)、若BG=5，AC=6，求△ABC的周长.

查看试题解析

抽取的排球数描取格品数	$500$	$1000$	$1500$	$2000$	$3000$
合格品数	$471$	$946$	$1425$	$b$	$2853$
合格品频率	$a$	$0.946$	$0.950$	$0.949$	$0.951$