湖南省湘西吉首市2024届高三下学期5月模拟数学试题

试卷更新日期：2024-06-03 类型：月考试卷

进入出卷网下载

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 已知全集 $U = {1 ， 2 ， 3 ， 4 ， 5}$ ，集合 $M = {1 ， 2} ， N = {3 ， 4}$ ，则 $∁_{U} (M ∪ N) =$ （）

A、{5} B、 ${1 ， 2}$ C、 ${3 ， 4}$ D、 ${1 ， 2 ， 3 ， 4}$

查看试题解析
2. 若复数 $z$ 满足 $i \cdot z = 3 - 4 i$ ，则 $| z | =$ （）

A、1 B、5 C、7 D、25

查看试题解析
3. 已知 $f (x) = s i n (ω x + ϕ)$ $(ω > 0)$ 满足 $f (\frac{π}{4}) = 1$ ， $f (\frac{5}{3} π) = 0$ 且 $f (x)$ 在 $(\frac{π}{4} ， \frac{5 π}{6})$ 上单调，则 $ω$ 的最大值为（）

A、 $\frac{12}{7}$ B、 $\frac{18}{17}$ C、 $\frac{6}{17}$ D、 $\frac{30}{17}$

查看试题解析
4. 已知 $f (x)$ 是定义域为 $(- ∞ ， + ∞)$ 的奇函数，满足 $f (1 - x) = f (1 + x)$ ．若 $f (1) = 2$ ，则 $f (1) + f (2) + f (3) + ⋯ + f (50) =$

A、 $- 50$ B、 $0$ C、 $2$ D、 $50$

查看试题解析
5. 甲､乙､丙､丁､戊5名志愿者参加新冠疫情防控志愿者活动，现有 $A, B, C$ 三个小区可供选择，每个志愿者只能选其中一个小区.则每个小区至少有一名志愿者，且甲不在 $A$ 小区的概率为（）

A、 $\frac{193}{243}$ B、 $\frac{100}{243}$ C、 $\frac{2}{3}$ D、 $\frac{5}{9}$

查看试题解析
6. 设 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和，若 $3 S_{3} = S_{2} + S_{4}$ ， $a_{1} = 2$ ，则 $a_{5} =$ （）

A、 $- 12$ B、 $- 10$ C、 $10$ D、 $12$

查看试题解析
7. 如图，一个棱长1分米的正方体形封闭容器中盛有V升的水，若将该容器任意放置均不能使水平面呈三角形，则V的取值范围是（）

A、 $(\frac{1}{6} ， \frac{5}{6})$ B、 $(\frac{1}{3} ， \frac{2}{3})$ C、 $(\frac{1}{2} ， \frac{2}{3})$ D、 $(\frac{1}{6} ， \frac{1}{2})$

查看试题解析
8. 直线 $x + y + 2 = 0$ 分别与 $x$ 轴， $y$ 轴交于 $A$ ， $B$ 两点，点 $P$ 在圆 ${(x - 2)}^{2} + y^{2} = 2$ 上，则 $△ A B P$ 面积的取值范围是（）

A、 $[2 ， 6]$ B、 $[4 ， 8]$ C、 $[\sqrt{2} ， 3 \sqrt{2}]$ D、 $[2 \sqrt{2} ， 3 \sqrt{2}]$

查看试题解析

二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．

9. 已知函数 $f (x)$ （ $x ∈ R$ ）是奇函数， $f (x + 2) = f (- x)$ 且 $f (1) = 2$ ， $f^{'} (x)$ 是 $f (x)$ 的导函数，则（）

A、 $f (2023) = 2$ B、 $f^{'} (x)$ 的一个周期是4 C、 $f^{'} (x)$ 是偶函数 D、 $f^{'} (1) = 1$

查看试题解析
10. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，点 $P$ 在线段 $B C_{1}$ 上运动，有下列判断，其中正确的是（）

A、平面 $P B_{1} D ⊥$ 平面 $A C D_{1}$ B、 $A_{1} P / /$ 平面 $A C D_{1}$ C、异面直线 $A_{1} P$ 与 $A D_{1}$ 所成角的取值范围是 $(0 ， \frac{π}{3}]$ D、三棱锥 $D_{1} - A P C$ 的体积不变

查看试题解析
11. 平面内到两定点距离之积为常数的点的轨迹称为卡西尼卵形线，它是1675年卡西尼在研究土星及其卫星的运行规律时发现的，已知在平面直角坐标系 $x O y$ 中， $M (- 2 ， 0)$ ， $N (2 ， 0)$ ，动点P满足 $| P M | \cdot | P N | = 5$ ，则下列结论正确的是（）

A、点 $P$ 的横坐标的取值范围是 $[- \sqrt{5} ， \sqrt{5}]$ B、 $| O P |$ 的取值范围是 $[1 ， 3]$ C、 $△ P M N$ 面积的最大值为 $\frac{5}{2}$ D、 $| P M | + | P N |$ 的取值范围是 $[2 \sqrt{5} ， 5]$

查看试题解析

三、填空题：本题共3小题，每小题5分，共15分．

12. $(2 + \frac{x}{y}) {(x - 2 y)}^{6}$ 的展开式中 $x^{4} y^{2}$ 的系数为.（用数字作答）

查看试题解析
13. 在△ABC中， $A B = 4 ， A C = 3 ， ∠ B A C = 90 ° ，$ D在边BC上，延长AD到P，使得AP=9，若 $\vec{P A} = m \vec{P B} + (\frac{3}{2} - m) \vec{P C}$ （m为常数），则CD的长度是．

查看试题解析
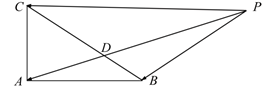14. 在同一平面直角坐标系中，P ， Q分别是函数 $f (x) = a x e^{x} - l n (a x)$ 和 $g (x) = \frac{2 l n (x - 1)}{x}$ 图象上的动点，若对任意 $a > 0$ ，有 $| P Q | \geq m$ 恒成立，则实数m的最大值为．

查看试题解析

四、解答题：本题共5小题，第15小题13分，第16、17小题15分，第18、19小题17分，共77分．解答应写出文字说明、证明过程或演算步骤．

15. 在锐角 $△ A B C$ 中，角A ， B ， C所对应的边分别为a ， b ， c ，已知 $\frac{s i n A - s i n B}{\sqrt{3} a - c} = \frac{s i n C}{a + b}$ ．

(1)、求角B的值；

(2)、若 $a = 2$ ，求 $△ A B C$ 的周长的取值范围．

查看试题解析
16. 为丰富学生的课外活动，学校羽毛球社团举行羽毛球团体赛，赛制采取5局3胜制，每局都是单打模式，每队有5名队员，比赛中每个队员至多上场一次且上场顺序是随机的，每局比赛结果互不影响，经过小组赛后，最终甲乙两队进入最后的决赛，根据前期比赛的数据统计，甲队明星队员 $M$ 对乙队的每名队员的胜率均为 $\frac{3}{4}$ ，甲队其余4名队员对乙队每名队员的胜率均为 $\frac{1}{2}$ .（注：比赛结果没有平局）

(1)、求甲队明星队员 $M$ 在前四局比赛中不出场的前提下，甲乙两队比赛4局，甲队最终获胜的概率；

(2)、求甲乙两队比赛3局，甲队获得最终胜利的概率；

(3)、若已知甲乙两队比赛3局，甲队获得最终胜利，求甲队明星队员 $M$ 上场的概率.

查看试题解析
17. 已知数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ， $a_{1} = - \frac{9}{4}$ ，且 $4 S_{n + 1} = 3 S_{n} - 9$ .

(1)、求数列 ${a_{n}}$ 的通项；

(2)、设数列 ${b_{n}}$ 满足 $3 b_{n} + (n - 4) a_{n} = 0 (n \in N^{*})$ ，记 ${b_{n}}$ 的前n项和为 $T_{n}$ ，若 $T_{n} \leq λ b_{n}$ 对任意 $n ∈ N^{∗}$ 恒成立，求实数 $λ$ 的取值范围.

查看试题解析
18. 如图，已知三棱柱ABC-A₁B₁C₁的底面是正三角形，侧面BB₁C₁C是矩形，M，N分别为BC，B₁C₁的中点，P为AM上一点，过B₁C₁和P的平面交AB于E，交AC于F.

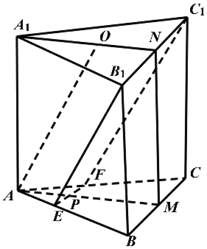(1)、证明：AA₁∥MN，且平面A₁AMN⊥EB₁C₁F；

(2)、设O为△A₁B₁C₁的中心，若AO∥平面EB₁C₁F，且AO=AB，求直线B₁E与平面A₁AMN所成角的正弦值.

查看试题解析
19. 双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左顶点为 $A$ ，焦距为4，过右焦点 $F$ 作垂直于实轴的直线交 $C$ 于 $B$ 、 $D$ 两点，且 $△ A B D$ 是直角三角形．

(1)、求双曲线 $C$ 的方程；

(2)、 $M$ 、 $N$ 是 $C$ 右支上的两动点，设直线 $A M$ 、 $A N$ 的斜率分别为 $k_{1}$ 、 $k_{2}$ ，若 $k_{1} k_{2} = - 2$ ，求点 $A$ 到直线 $M N$ 的距离 $d$ 的取值范围．

查看试题解析