【培优卷】2024年浙教版数学七年级下册第6章数据与统计图表 单元测试
试卷更新日期：2024-06-02 类型：单元试卷
一、选择题（每题3分，共30分）
-
1. 在频数直方图中，共有7个小长方形，若中间一个小长方形的面积等于其他6个小长方形的面积的和的 ， 且共有100个数据，则中间这一组数据的频数是（ ）A、25 B、20 C、0.25 D、0.22. 为了了解噪声污染的情况，某市环保局抽样调查了80个测量点的噪声声级(单位：分贝)，并进行整理后分成五组，绘制出频数分布直方图，如图所示．已知从左至右前四组的频率分别是0.15，0.25，0.3，0.2，且噪声声级高于69.5分贝就会影响工作和生活，那么影响到工作和生活而需对附近区域进行治理的测量点有（ ）
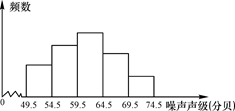A、5个 B、8个 C、12个 D、15个3. 某校公布了该校各年级学生体育达标情况的两张统计图（如图），该校七、八、九年级共有学生 800人.甲、乙、丙三个同学看了这两张统计图后，甲说：“七年级学生的体育达标率最高.”乙说：“八年级共有264人.”丙说：“九年级学生的体育达标率最高.”甲、乙、丙三个同学的说法中，正确的是 （ ）
A、甲和乙 B、乙和丙 C、甲和丙 D、只有丙4. 为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查.已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：身高情况分组表(单位：cm)
组别
A
B
C
D
E
身高
x＜155
155≤x＜160
160≤x＜165
165≤x＜170
x≥170
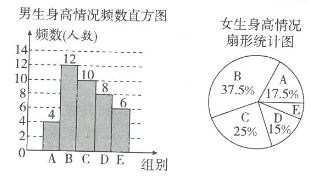
根据图表提供的信息，样本中，身高在160≤x＜170之间的女学生人数为（ ）
A、8 B、6 C、14 D、165. 为了解游客在西湖景区、西溪湿地、良渚遗址公园和杭州运河公园这四个风景区旅游的满意度，数学小组的同学商议了几个收集数据的方案：方案一：在多家旅游公司调查400名导游；方案二：在西湖景区调查400名游客；方案三：在西溪湿地调查400名游客；方案四：在上述四个景区各调查100名游客.
在这四个收集数据的方案中，最合理的是（ ）
A、方案一 B、方案二 C、方案三 D、方案四6. 在“体育中考”的某次模拟测试中，某校某班10名学生测试成绩统计如图．对于这10名学生的参赛成绩，下列说法中错误的是（ ）
A、众数是28 B、中位数是28 C、平均数是27.5 D、极差是87. 九（1）班班长统计去年1～8月“书香校园”活动中全班同学的课外阅读数量（单位：本），绘制了如图所示的折线统计图，与上月比较阅读数量变化率最大的月份是（ ）
A、2月 B、5月 C、6月 D、7月8. 某电商网站以智能手表为主要的产品运营．今年1—4月份，该网站智能手表的销售总额如图1所示，其中一款通话功能智能手表的销售额占当月智能手表销售总额的百分比如图2所示．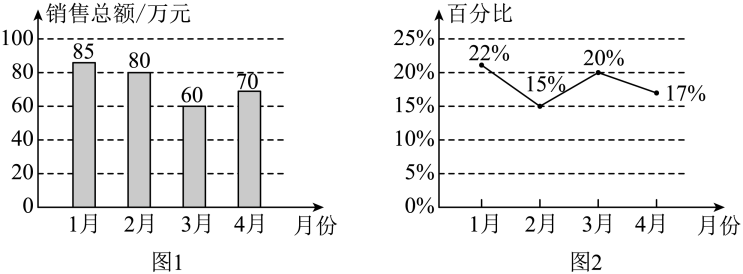
以下四个结论正确的是（ ）
A、今年1—4月，智能手表的销售总额连续下降 B、今年1—4月，通话功能智能手表的销售额在当月智能手表销售总额中的占比连续下降 C、通话功能智能手表3月份的销售额与2月份的销售额持平 D、今年1—4月，通话功能智能手表销售额最低的月份是2月9. 某校公布了该校反映各年级学生体育达标情况的两张统计图（如图），该校七、八、九三个年级共有学生1000人．甲、乙、丙三个同学看了这两张统计图后，甲说：“七年级的体育达标率最高．”乙说：“八年级共有学生330人．”丙说：“九年级的体育达标率最高．”甲、乙、丙三个同学中，说法正确的是（ ）
A、甲和乙 B、乙和丙 C、甲和丙 D、甲和乙及丙10. 某公司在抗震救灾期间承担40 000顶救灾帐篷的生产任务，分为A、B、C、D四种型号，它们的数量百分比和每天单独生产各种型号帐篷的数量如图所示：
根据以上信息，下列判断错误的是（ ）
A、其中的D型帐篷占帐篷总数的10% B、单独生产B型帐篷的天数是单独生产C型帐篷天数的3倍 C、单独生产A型帐篷与单独生产D型帐篷的天数相等 D、单独生产B型帐篷的天数是单独生产A型帐篷天数的2倍二、填空题（每题4分，共24分）
-
11. 某校体育小组为了了解全校学生“最喜欢的一项球类项目”，随机抽取了部分学生进行调查，如图是根据调查结果绘制的不完整的统计图，由统计图可知，在扇形统计图中，“乒乓球”所对应的扇形圆心角的度数为°.
12. 某校九(2)班的学生在植树节开展“植树造林，绿化城市”的活动，本次活动结束后，该班植树情况的部分统计图如图所示，那么该班的总人数是.
13. 为监测某河道水质，某探究小组对该河道进行了6次水质检测，绘制了如图所示的氨氮含量折线统计图．若这6次水质检测中氨氮含量的平均数为1.5 mg/L，则第3次检测得到的氨氮含量是 mg/L．
14. 在一次生活垃圾分类知识竞赛中，某校七、八年级各有100名学生参加，已知七年级男生成绩的优秀率为40%，女姓成绩的优秀率为60%；八年级男生成绩的优秀率为50%，女姓成绩的优秀率为70%．对于此次竞赛的成绩，下面有三个推断：①七年级成绩优秀的男生人数小于八年级成绩优秀的男生人数；
②七年级学生成绩的优秀率一定小于八年级学生成绩的优秀率；
③七、八年级所有男生成绩的优秀率不一定小于七、八年级所有女生成绩的优秀率．
其中合理的推断是(填序号)
15. 如图是小亮根据全班同学喜欢的四种球类运动的人数绘制的两幅不完整的统计图（全班每位同学在这四种球类中选一种），则喜欢“乒乓球”的人数是人．
16. 如图是某市2016- 2019年私人汽车拥有量和年增长率的统计图，该市私人汽车拥有量年净增量最多的是年，私人汽车拥有量年增长率最大的是年．
三、解答题（共8题，共66分）
-
17. 以下数据是某同学在街头随机询问所获得的一批青年对自己现在所从事工作的满意度评分，其中1表示很不满意，2表示不满意，3表示一般，4表示满意，5表示很满意.
2 5 4 5 2 5 3 1 2 3
4 4 3 3 5 2 1 4 3 3
3 4 4 2 5 5 4 4 4 2
3 2 4 3 3 5 1 1 5 3
4 1 2 2 3 4 3 3 1 4(1)、这组数据是通过什么方法获得的?(2)、为了更清楚地反映青年对自己工作的满意度情况，你认为应该怎样整理这些数据?(3)、从数据中可以得出什么结论?18. 为了参加全校各年级之间的广播操比赛，七年级准备从63名同学中挑选身高差不多的40名同学参加比赛．为此收集到这63名同学的身高（单位：cm），并绘制了频数分布表和频数分布直方图．身高分组
频数
2
a
23
13
9
3
根据以上信息，解答下列问题：
(1)、请根据题中已有信息写出a的值，并补全频数分布直方图；(2)、此绘制选择的组距为；(3)、体育委员认为依据此频数分布直方图不能很好地解决这个问题，请你分析他的理由，并写出如何调整可能会更好．19. 学校为了更合理地配置体育运动器材和场地，需要了解同学们对各种球类运动的喜好程度，故组织全校学生做一次问卷调查（每人选一种），并制作统计图如图所示.
(1)、全校共有多少名学生参与调查？请补全条形统计图.(2)、根据各项球类运动受同学们喜爱的程度，对学校提出2条有关体育运动器材和场地配置的建议.20. 在校园艺术节活动中，同学们踊跃参加各项竞赛活动，参加的学生只能从“歌曲”，“舞蹈”，“小品”，“主持”和“乐器”五个选项中选择一项．现将选择情况绘制成了条形统计图和不完整的扇形统计图，其中条形统计图部分被不小心污染．请根据统计图中的相关信息，回答下列问题：
(1)、图1中，根据数据信息可知：参加“主持”比赛的人数是参加“乐器”比赛人数的倍，而统计图表现出来的直观情况却是：参加“主持”比赛的人数是参加“乐器”比赛人数的3倍，两个结果之所以不一样，是因为；(2)、请求出全校一共有多少名学生参加“舞蹈”比赛？(3)、在图2中，“小品”部分所对应的圆心角的度数为度；(4)、拟参加比赛活动的学生有获奖，其中获二等奖与三等奖的人数之比 ， 二等奖人数是一等奖人数的1.5倍，直接写出获一等奖的学生有人．21. 为迎接杭州亚运会的召开，某校决定在全校范围内开展亚运知识的宣传教育活动为了了解宣传效果，随机抽取部分学生，并在活动前、后对这些学生进行了两次跟踪测评，两次测评中所有同学的成绩没有低于分，现在将收集的数据制成频数分布直方图每一组包含左端值，不包含右端值和频数表宣传活动后亚运知识成绩频数表：
成绩
频数
(1)、本次活动共抽取学生 ；(2)、宣传活动前，在抽取的学生中成绩人数最多一组的组中值是 分；(3)、表中的 ，宣传活动后，在抽取的学生中分数高于分的至少有 人，至多有 人；(4)、小聪认为，宣传活动后成绩在的人数为 ， 比活动前减少了人，因此学校开展的宣传活动没有效果请你结合统计图表，说一说小聪的看法是否正确为什么？22. 目前，国际上常用身体质量指数“”作为衡量人体健康状况的一个指标，其计算公式：（G表示体重，单位：千克；h表示身高，单位：米）．已知某区域成人的数值标准为：为瘦弱（不健康）；为偏瘦；为正常；为偏胖；为肥胖（不健康）．某研究人员从该区域的一体检中心随机抽取60名成人的体重、身高数据组成一个样本，计算每名成人的数值后统计如下：身体属性
人数
瘦弱
3
偏瘦
8
正常
11
偏胖
9
肥胖
m
（男性身体属性与人数统计表）
(1)、这个样本中身体属性为偏胖的人数是人；(2)、某男性的体重为64.8千克，身高为1.8米，该男性的数值为；(3)、当且（m、n为正整数）时，求这个样本中身体属性为不健康的男性人数与身体属性为不健康的女性人数的比值．23. 中国是世界文明发源地之一，是举世闻名的礼仪之邦．一个民族，之所以在世界文明？之林享誉千年，在于它独特而充满魅力的文化．为了弘扬优秀传统文化，某中学举办了传统文化知识大赛（全体同学都参为），其规则是：每位参赛选手回答100道选择题，答对一题得1分，不答或错答得0分，赛后抽取部分参赛选手的答题成绩（单位：分）进行了相关统计，整理并绘制成如下的统计图表：
组别
成绩
频数（人）
百分比
1
30
2
45
15%
3
60
4
40%
5
45
15%
请根据以上信息，解答下列问题：
(1)、表中 ， ， ；(2)、补全频数分布直方图；(3)、如果将其绘制成扇形统计图，请求出参赛成绩不低于90分这组所在扇形圆心角的度数．24. 八年级某班同学为了了解2018年某居委会家庭月均用水情况，随机调查了该居委会部分家庭月均用水量，并列出下面的频数分布表：月均用水量
频数（户
6
12
16
10
4
2
请解答以下问题：(1)、这次随机调查了该居委会 户，把频数分布直方图补充完整；(2)、求该居委会用水量不超过的家庭占被调查家庭总数的百分比；(3)、若该居委会有1000户家庭，根据调查数据估计，该小区月均用水量超过的家庭大约有多少户？